Типы случайных величин

Элементы теории вероятности

Закономерности случайных явлений проявляются при их многократном воспроизведении. В случае устойчивых закономерностей, говорят об однородности случайных явлений. Результат каждого эксперимента называют исходом. Любой мысленно возможный, неразложимый результат называется элементарным исходом или элементарным событием. Множества элементарных событий называют пространством элементарных событий . Суммой событий называют явление, когда происходит хотя бы одно из двух событий. Произведение событий называют явление, когда происходят оба события. Если из экспериментов событие произошло раз, то называют абсолютной частотой этого события, а – относительной частотой. Вероятностью случайного события 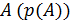называется числовая функция, определенная на пространстве элементарных событий , и удовлетворяющая следующим аксиомам Колмогорова:

1)

2)

3) , в случае, если не равно пустому множеству, (i,j=1,∞). Т.е. вероятность наступления счетного множества попарно несовместимых событий равна сумме этих событий.

 

 

Теорема сложения вероятностей:

 

 

Теорема умножения двух вероятностей:

 

 

Теорема умножения нескольких вероятностей:

 

 

Формула полной вероятности

Является следствием теорем сложения и умножения вероятностей. Здесь рассматривается вероятность случайного события , зависящего от множества гипотез

 

Формула Байеса

Применяется для переопределения вероятности гипотез, сопутствующих некоторому произошедшему событию, при этом переопределяемая вероятность называется апостериорной, а известная вероятность – априорной

 

 

Последовательность независимых испытаний, схема Бернулли

Повторные испытания называются независимыми, если вероятности их исходов не зависят от исходов предыдущих испытаний.

Испытаниями Бернулли называют повторные независимые испытания, в каждом из которых возможны два исхода – успех или неудача, вероятности которых не изменяются.

Схемой Бернулли называют проведение заранее установленного числа испытаний Бернулли.

 

Результатом схемы Бернулли является число успехов во всей серии испытаний.

 

Наиболее вероятным числом успехов в схеме Бернулли, называется число :

 

Обычно определяется неравенством

 

При очень большом числе испытаний, и очень малой вероятности успеха, если произведение , то вероятность успехов в схеме Бернулли оценивают следующим пределом:

 

При больших вероятность того, что число успехов

где

А

 

 

Типы случайных величин

Дискретной называется случайная величина, которая в результате эксперимента может принимать определенное значение, совокупность которых представляет собой конечное / счетное множество.

Сумма вероятностей принятия случайной величиной всех ее возможных значений .

 

Законом распределения дискретной случайной величины называется правило / зависимость, которое каждому возможному значению ДСВ ставит вероятность его появления.

 

Функция распределения 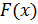случайной величины называется вероятность того, что будет ,

 

Свойства функции распределения:

1)

2)

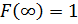
3)

4)

5) Непрерывность (для непрерывных СВ (НСВ)), разрывная ступенчатость (для ДСВ)

 

Плотностью распределения НСВ называется производная ее функции распределения.

 

Свойства плотности распределения:

1)

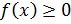
2)

3)

4)

 

 

Дисперсия СВ = Матожидание[кси]² – Матожидание²[кси] = СУММА(i=1,n)x_i²*p(x_i-кси)-М²[кси] =

ИНТЕГРАЛ(-inf, +inf)x²f(x)dx – M²[кси]

 

Свойства дисперсии:

D[кси] >= 0

D[alpha] = 0

D[alpha * ksi] = alpha * D[ksi]

D[ksi +- eta] = D[ksi] + D[eta] +- 2M_{ksi eta}(корелляционный момент)

M_{ksi eta} = M[(ksi – M[ksi])(eta – M[eta])] – для зависимых СВ

M_{ksi eta} = 0 – для независимых СВ

D[ksi +- eta] = D[ksi] + D[eta]

D[alpha + ksi] = D[ksi]

D[ksi*eta] = D[ksi] * D[eta] + D[eta]*M²[ksi] + D[ksi] * M²[eta]

 

Средним квадратичным отклонением (СКО) СВ называется положительное значение квадратного корня из дисперсии СВ

Sigma[ski] = +SQRT[D[ksi]]

СКО характеризует степень разброса случайной величины в окрестностях матожидания

 

Коэффициент вариации СВ

V[ksi] = Sigma[ksi]/M[ksi]

Моментов СВ k-ого порядка называют величину M[(ksi – a)^k], где a – константа

Если a = 0, то моменты называют начальными M[ksi^k] = nu_k

Если a=M[ksi], то моменты называют центральными M[(ksi – M[ksi])^k] = mu_k

Nu₀ = M[ksi⁰] = 1; mu₀ = 1

Nu₁ = M[ksi]; mu₁ = M[ksi – M[ksi]] = 0

Nu₂ = M[ksi²]; mu₂ = D[ksi]

 

Начальные и центральные моменты связаны следующими отношениями

Mu₂ = nu₂-nu₁²

Mu₃ = nu₃ – 3nu₂nu₁ + 2nu₁²

Mu₄ = nu₄ – 4nu₃nu₁ + 6nu₂nu₁² – 3nu₁²

 

Коэффициентом ассиметрии распределения СВ ksi называется

beta₁[ksi] = mu₃/sigma³ = M[(ksi-M[ksi])³]/sigma³

 

Коэффициент эксцесса

Beta₂[ksi] = mu₄/sigma⁴ – 3

Beta₂[ksi] = 0 для нормального распределения

Дискретные случайные величины:

Биномиальное распределение

СВ Х имеет биномиальный закон распределения, B_i[n, p], если она дискретна, и означает число успехов в схеме n испытаний Бернулли.

P(x=k) = P_n(k) = C_n^kp^kq^n-k

Характеризуется числом испытаний n и вероятностью успеха P в этом испытании

Основные числовые характеристики:

M[x] = np

D[x] = np(1-p)

Эквивалентом моды является ближайшее значение к величине (n+1)*p – 0.5

 

Распределение Пуассона

n -> inf

p -> 0

np = const = lambda

P(x=k) = lambda^k/k! * e^-lambda

Ближайшее значение к Lambda = 0.5

Основные характеристики:

M[x] = D[x] = lambda

 

Геометрическое распределение

СВ х имеет геометрический закон распределения, если она дискретна и определяет число независимых испытаний Бернулли, предшествующих первому появлению успеха

 

P[x=k] = (1-p)^k*p

 

 

Непрерывные случайные величины

Равномерное распределение

Непрерывная СВ имеет равномерный или прямоугольный закон распределения R(a, b), если она принимает равновероятные значения на отрезке от A до B

f(x) = {1/b-a, x принадлежит [a; b]; 0, x не [a;b]}

F(x) = {x-a/b-a, x принадлежит [a; b]; 1, x > b }

M[x] = med(x) = (a+b)/2

D[x] = (b-a)²/12

Mod [x]

Beta1[x]=0

 

Показательное (экспоненциальное) распределение

СВ х имеет показательное распределение, если она непрерывна, принимает только аоложительные значения и характеризуктся следующими функциями

f(x) = {0, x <= 0; lambda*e^-lambda*x, x > 0}

F(x) = {0, x <= 0; 1-e^{-lambda x,} x > 0}

 

 

Основные числовые характеристики

M[x] = sigma[x] = 1/lambda

Mod [x] = 0

Med[x] = ln2/lambda

D[x] = 1/lambda²

 

Распределение Эрланга

Пусть есть последовательность СВ

x₁, x₂, …, x_k, имеющих показательный закон распределения с параметром lambda_i = lamda = const,

тогда СВ х = x₁ + x₂ + … + x_k имеет распределение Эрланга k-того порядка с параметром lambda, тогда x непрерывна и принимает только положительное значение

f(x) = {0, x<= 0; lambda^kx^k-1e^-lambda*x/(k-1)!, x > 0}

Для k = 1 совпадает с показательным распределением

M[x] = k/lambda

Mod[x] = (k-1)/lambda

D[x] = k/lambda²

 

Распределение Вейбулла

СВ х имеет распределение Вейбулла

W(alpha, lambda), alpha > 0, lambda > 0

Если x непрерывна, положительна и имеет функцию распределения

f(x) = {0, x <= 0; alpha*lambda*x^alpha-1*e^{-lambda*x^alpha}, x > 0}

При alpha = 1 совпадает с показательным распределением

Числовые характеристики:

M[x] = alpha^1/2Gamma(1+1/alpha), где Gamma – гамма функции / интеграл Эйлера второго рода

Mod[x] = {0, alpha <= 1; (1 – (1/alpha)/lambda)^1/alpha, alpha > 1}

D[x] = lambda^-2/lambda{2/alpha*Gamma(2/alpha)-alpha^-2*Gamma²(1/alpha)}

 

Нормальное распределение

Случайная величина X имеет нормальное или Гауссовский закон распределения, обозначаемый N(m, sigma), если она имеет

F(x) = 1/(sigma*sqrt(2*pi)) Integral(-inf, x)(e^(-(t-m)^2/(2*sigma^2)))dt

f(x) = 1/(sigma*sqrt(2*pi))*e^(-(x-m)^2/(2*sigma^2))

M[x] = m;

sigma[x] = sigma

D[x] = sigma^2

Mod[x] = med[x] = m

Beta₁[x] = beta₂[x] = 0

F(x)

 

Стандартной нормальной случайной величиной называется нормальная случайная величина N(0,1)

N(x) = 1/SQRT(2*Pi) Integral(-inf,x)(e^-(t^2/2))dt

 

Хи-квадрат распределение (X²)

Если случайные величины x₁, x₂, …, x_n независимы, то и имеют стандартное нормальное распределение, то случайная величина Xи² = x₁²+x₂²+…+x_n² имеет распределение Xи² с n степенями свободы.

f(Хи²) = {0, Хи² <= 0; 1/2^(n/2*GAMMA(n/2)) Хи^(n/2 - 1)e^-Хи/2, Хи > 0}

F(Хи²) = {0, Хи <= 0; 1/2^(n/2*GAMMA(n/2)) Integral(0,Хи)(t^(n/2 - 1)e^(-Хи/2)dt), Хи > 0}

GAMMA = Гамма функции / Интеграл Эйлера второго рода.

 

 

Распределение Стьюдента

Если случайные величины x₁, x₂, …, x_n независимы и имеют стандартное нормальное распределение, то t распределением или распределением Стьюдента с n степенями свободы называется случайная величина, вычисляемая как

t = x₀/SQRT(1/n)*SUM(i=1,n)x_i², где x₀ также нормально распределенная случайная величина.

f(t) = (GAMMA((n+1)/2)/(/SQRT(Piⁿ)GAMMA(n/2)))*(1+t²/n)^-(n+1)/2

 

Распределение Фишера

СВ x1, x2, …, xn и eta₁, eta₂, …, eta_n независимы и стандартно нормально распределены, тогда распределение Фишера с m и n степенями свободы, тогда

F = (1/m* SUM(i=1,m)x_i²)/(1/n*SUM(i=1,n)(eta_i²))

f(x)={0,x<=0;((GAMMA(m+n/2)m^(m/2)*n^(n/2)*x^(m/2-1))/(GAMMA(m/2)*GAMMA(n/2)))*(m+n*x)^-(m+n/2), x > 0}

 

Основные понятия математической статистики

1) Выборочный метод при исследовании вероятностных систем

Множество всех исследуемых объектов (возможных результатов наблюдений), называется генеральной совокупностью. Генеральная совокупность наблюдений случайной величины должна иметь некоторое распределение и характеризоваться некоторыми математическими параметрами. На практике получение генеральной совокупности невозможно. Ограничиваются совокупностью наблюдений, называемой выборкой. Количество наблюдений называется объемом выборки. Каждое наблюдение, входящее в выборку, называется элементом выборки.

Выборочным методом называется получение оценок, свойств случайной величины по выборке.

Для того, чтобы по выборке можно было делать выводы о свойствах изучаемой случайной величины, выборка должна удовлетворять следующим требованиям:

- достаточный объем;

- репрезентативность / представительность (хорошее отражение свойств всей совокупности);

- независимость испытаний друг от друга;

 

Основные цели выборочного исследования:

- проверка предположения о виде распределения случайной величины;

- оценка числовых характеристик случайной величины и параметров функции распределения;

- проверка согласованности гипотезы о виде распределения исследуемой случайной величины с опытными данными;

 

Первичной формой представления статистического материала является статистический ряд, в котором элементы выборки x₁, x₂, …, x_n указываются в порядке их появления.

В целях обработки статистический ряд упорядочивают. Неубывающие последовательности {x_i} называются вариационным рядом. Если эта последовательность дискретна, то для каждого ее значения вычисляется относительная частота Nu_i = m_i/n. Для непрерывной случайной величины выполняют группировку значений вариационного ряда по интервалу.

Эмпирической функцией распределения случайной величины X называется функция F^*(X), которая определяет для каждого x_i относительную частоту события x_i < X.

F*(X) = n(x_i < X)/n

F*(X) является опытным аналогом F(X). Для нее выполняются все свойства функции распределения, но, при этом, она является ступенчатой функцией. Ступени совпадают со значением x_i.

 

Элементы статистического оценивания результатов исследования.

Задача оценивания неизвестного параметра Тэта распределения случайной величины, н-р, M[x], sigma[x], и т.д. состоит в построении функции

Найденное значение этой функции , называют оценкой параметра . Поскольку выборка имеет ограниченный объем, а элементы ее случайны, то сами оценки – это также случайные величины.

 

Два вида оценок:

- точечная, которая характеризует оцениваемый параметр одним числом;

- интервальная, 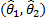, которые являются границами интервала, покрывающего значеника явле параметра с какой-то заданной вероятностью .

 

Точечная оценка называется состоятельной, если при увеличении числа испытаний, она сходится по вероятности к значению оцениваемого параметра. Она называется несмещенной, если ее матожидание равно значению оцениваемого параметра .

Точечная несмещенная оценка параметра называется эффективной, если она обладает минимальной дисперсией.

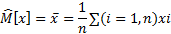
Оценка точечная и несмещенная.

Если x имеет нормальное распределение, то оценка является эффективной.

 

Для оценки моды дискретной случайной величиный используется значение сгруппированного статистического ряда , которому соответствует наибольшее значение частоты.

Оценкой медианы является серединный член вариационного ряда.

 

Интервальные оценки

В силу случайности точечных оценок, неизвестно, насколько они отличаются от реальных параметров случайной величины, поэтому в реальных исследованиях пользуются интервальными оценками.

Доверительной вероятностью оценки параметра является вероятность p_{дов (доверительное)} выполнения неравенства . Интервал называют доверительным интервалом.

 

Общий алгоритм построения доверительного интервала

1. По выборке множества x_i объема n определяется точечная оценка числовой характеристики theta

2. определяется вспомогательная случайная величина, она же выборочная статистика , связанная с параметром и имеющая известную функцию плотности распределения .

3. Для заданной доверительной вероятности p_дов = 1-alpha, где alpha называется уровнем значимости, находят интервал от y₁ до y₂, для которого справедливо равенство, что p(y₁ < eta < y₂) = p_дов.

4. Проводят обратные преобразование величины eta к величине theta и находят интервал theta₁^, theta₂^, для которого вероятность попадания theta в него равна p_дов. P(theta₁^ < theta < theta₂^)

 

 

Примеры:

Проверка гипотезы о значении матожидания случайной величины с известным СКО.

Если гипотеза H0 верна, то U примет значение, близкое к нулю. Если верна альтернативная гипотеза (), то U примет значение не близкое к нулю.

Размер ОКЗ (область критических значений)

Значение статистического критерия определяется из , где - квантиль стандартного альфа распределения.

Вычисляется выборочное значение

Гипотеза H0 считается выполняющейся, если -Ualpha/2 < U^ < Ualpha/2

 

Проверка гипотезы о значении матожидания случайной величины с неизвестным СКО.

Имеющая распределения Стьюдента с n степенями свободы. Если H0 верна, то t примет значение близкое к нулю.

Критическое значение t _стат определяются как квантиль распределения Стьюдента уровня альфа\2,n-1

Гипотеза H0 считается согласующейся с результатами экспериментов, если t _стат удовлетворяет условию.

 

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: