 |
Моделирование дискретных распределений.
|
|
|
|
Биноминальное распределение
Моделируется путем подсчета количества единиц в коде псевдослучайного двоичного числа 
. Эта величина имеет биноминальное распределение. 
.
Геометрическое распределение
Вида 
При этом находят номер испытания 
, которое принесет первый успех для появления события 
с вероятностью 
. Для этого последовательно обращаются к ГПСП и моделируют очередное , и проверяют выполнимость жребия первого типа.
Распределение Пуассона
Для моделирования распределения Пуассона 
обращаются последовательно к ГПСП, получают очередное значение и проверяют выполнимость неравенства:
Как только это неравенство выполнится, сумма будет иметь распределение Пуассона с параметром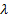 
.
Основные понятия планирования экспериментов на ЭВМ с использованием моделей вероятностных систем.
Основными компонентами моделей сложной системы являются:
- Множество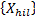 
Значение вектора входной информации, формируемый в соответствии с 
-тыми функциями распределения в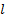 
‑той реализации 
-того варианта исследования системы.
- Множество 
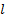Значение вектора начального условия -того варианта -той реализации модели в соответствии с 
-той функцией распределения.
- Множество 
Значение вектора параметров -того варианта модели системы, формируемой в соответствии с 
-той функцией распределения в 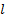-той реализации.
На систему воздействует также множество неуправляемых переменных 
- К ним так же могут быть отнесены вектор неконтролируемых случайных воздействий 
, и, в некоторых случаях, 
.
Выходными характеристиками моделей является вектор откликов 
и обобщенный показатель 
.
Назовем 
и 
факторами, конкретное значение каждой компоненты их назовем уровнем фактора.
|
|
|
Первичными факторами назовем те входные переменные и параметры модели, изучение которых необходимо исследователю, остальные назовем вторичными.
Моделирование сложной системы преследует следующие цели:
1. Оценка вида зависимостей откликов и состояний системы от ее предыдущих состояний по данным натурного или модельного эксперимента;
2. Нахождение сочетаний входных параметров и выходных переменных, которые обеспечивают максимум обобщенного показателя ;
3. Изучение динамики изменения состояний системы в виде множества состояний и поиск узких мест в структуре модели.
Преимущественно, модели предпочитают формировать аналитически в виде относительно простых полиномов.
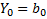полином 
степени
полином 
степени
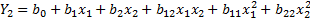полином 
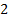степени
Определяют план эксперимента (ПЭ), представляющий собой совокупность данных, определяющих число, условие и порядок реализации опыта.
Планирование эксперимента устанавливает совокупность действий по разработке тактики эксперимента от начальных до заключительных этапов изучения системы.
Точкой плана называют упорядоченную совокупность значений факторов, соответствующих условиям проведения опыта.
Общая совокупность множества параметров, описывающих действия плана, называется спектром плана.
Методы векторной оптимизации сложных систем. Применительно к задаче оптимизации вариантов компьютерного моделирования.
Во многих случаях возникает задача оптимизации результатов моделирования по совокупности откликов модели. Поскольку используется множество откликов в качестве критерия оптимизации, такая оптимизация называется векторной и многокритериальной. Фактически, имеется не одно, а множество решений, каждый из которых может быть избран в качестве оптимального.
|
|
|
