Учет рисков при обосновании рисковой премии

Международная методика ЮНИДО предусматривает определение рисковой премии, учитываемой при формировании нормы дохода. Такой механизм учета риска при оценке эффективности позволяет предотвратить

реализацию проектов, общая доходность которых неоправданно завышена. Учет риска при формировании нормы дохода обязателен, поскольку наиболее отражает реальные условия реализации проекта.

Выделяют статистический и экспертный методы обоснования рисковой премии в составе нормы дохода. Выбор определяется существованием статистической закономерности наступления рискового события. Прежде всего так можно оценивать риски, связанные с надежностью работы оборудования, качеством выпускаемой продукции, поскольку возможно получение информации о вероятности отказов, аварий при эксплуатации, браке и других потерях. Статистические закономерности можно установить по природным рискам, связанным со стихийными бедствиями, авариями.

При этом необходимо учитывать, что отдельные виды рисков, характеризующиеся статистической закономерностью проявления, могут быть учтены в оценке эффективности при формировании исходной экономической информации в ходе разработки системы мероприятий, рассмотренных в п. 8.4.2. Поэтому необходимо избегать повторного учета риска в схеме расчета эффективности, иначе требования инвестора к эффективности проекта окажутся завышенными.

Использование статистического метода оценки риска возможно на основе поэлементного или агрегированного подходов. Первый учитывает каждый вид риска в отдельности: определяет номенклатуру рисков, подлежащих отражению в норме дохода, оценивает влияние каждого из них на величину рисковой премии. С помощью агрегированного метода рисковая премия оценивается укрупненно по всем видам рисков.

Рассмотрим теоретические основы реализации статистического метода оценки риска при формировании рисковой премии.

Риск — вероятностная категория. Поэтому прежде всего его измеряют как вероятность возникновения того или иного уровня потерь (наступления какого-то события).

Оценивая вероятность получения определённого уровня прибыли, можно построить кривую вероятностей возникновения определенного уровня потерь, которую называют кривой риска (рис. 8.4).

В точке В прирост прибыли равен 0. Вероятность нулевых потерь максимальна, но меньше 1. В точке В_д — полная потеря прибыли. В точке В_кр — вероятность полной потери выручки. В точке В_кат — потеря имущества. Потери, превышающие имущественное состояние, не рассматриваются, так как их невозможно взыскать.

Ориентировочно считается, что предельные значения показателей риска— В_д=0,1; В_кр =0,01; В_кат = 0,001. Это означает, что не следует

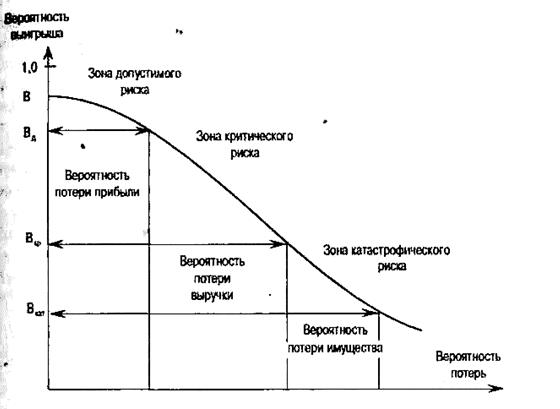
Рис. 8.4. Вероятность наступления риска

осуществлять инвестиции, если в десяти случаях из ста можно потерять прибыль, в одном случае из ста потерять выручку и хотя бы в одном случае из тысячи потерять имущество.

Кривые риска можно строить на основе статистического, экспертного и расчетно-аналитического методов.

Статистический метод состоит в изучении статистики потерь, имевших место в аналогичных случаях, при этом устанавливается частота появления таких потерь. Если статистический массив представителен, частоту возникновения определенного уровня потерь (деление числа соответствующих случаев на общее количество результатов аналогичных инвестиционных проектов) можно приравнять к вероятности их возникновения и построить кривую риска.

Экспертный метод применяется, если специалисты оценивают уровень и вероятность потерь в трех характерных точках: допустимых, критических и катастрофических потерь. По ним можно ориентировочно воспроизвести всю кривую риска.

Расчетно-аналитический метод построения кривой риска базируется на принципах теории вероятностей. Для измерения общего риска при инвестировании используется ряд показателей из области

математической статистики. Прежде всего это показатель вариации ((f), который измеряет дисперсию (отклонение) вокруг ожидаемой средней величины показателя экономической эффективности инвестиций (математическое ожидание случайной величины). Чем больше вариация, тем больше дисперсия или разбросанность по сравнению с ожидаемым средним значением. Так как данный способ оценки риска используется для определения рисковой премии, добавляемой к норме дохода, в качестве показателя экономической эффективности, вокруг которого измеряется вариация, целесообразно использовать внутреннюю норму дохода или рентабельность капитала, также измеряемые в процентах.

Вариация представляет собой сумму квадратных отклонений (девиаций) от средней величины — ожидаемого значения показателя экономической эффективности инвестиций, взвешенных по вероятности каждой девиации.

Так как вариация измеряется в тех же единицах, что и показатель эффективности, но возведенных в квадрат, оценить экономический смысл вариации для инвесторов затруднительно. Поэтому в качестве альтернативного показателя риска обычно используют показатель стандартной девиации (σ) (среднее квадратичное отклонение), который является квадратным корнем вариации:

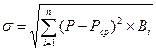, (8.1)

где п — число наблюдений;

Р — расчетное значение показателя эффективности инвестиций при различных состояниях внешней и внутренней среды проекта, т. е. с учетом рисков;

Р_ср —среднее ожидаемое значение показателя эффективности проекта (математическое ожидание);

B_j — значение вероятности, соответствующее Р, определяется так:

. (8.2)

Здесь К_i — количество случаев наступления соответствующих событий;

п — общее количество учтенных результатов.

Стандартная девиация показывает, насколько в среднем каждый возможный вариант значения показателя эффективности отличается от его средней величины, т. е. характеризует абсолютную величину риска.

Эти показатели используют как меру риска. Чем больше вариация, тем в среднем больше отклонение, т. е. выше неопределенность и риск.

Если вариация равна 0, то эффективность не отклоняется от ожидаемого значения, т. е. нет неопределенности и риска.

Следующий показатель риска — коэффициент вариации (CV):

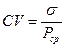(8.3)

Пример 8.1«. Выбор менее рискованного инвестиционного проекта и обоснование рисковой премии с помощью статистического метода оценки риска

Возможны два альтернативных варианта инвестирования 100 тыс. р. сроком на 1 год и пять возможных сценариев надежности работы оборудования в прогнозируемом периоде, характеризующихся различным уровнем риска. Данные сценарии основаны на статистической информации о поломках оборудования в предыдущие периоды в аналогичных ситуациях. Наступление каждого из вариантов с определенной вероятностью имеет соответствующую внутреннюю норму дохода (табл. 8.1).

Вероятность получения максимального дохода (26%) по проекту 2 при условии наступления сценария 5 равна 5%. Средневзвешенная ожидаемая ВНД по каждому варианту инвестирования определяется как сумма произведений вероятностей и соответствующей ВНД.

Оценка риска для двух альтернативных вариантов инвестиций приведена в табл. 8.2.

Таблица 8.1. Расчет ожидаемой внутренней нормы дохода (ВНД) и показателей риска

Сценарий	Количество случаев наступления результата (Ki)	Вероятность (Вi)	ВНД по инвестициям Рi	Pi – Рср	(Рi – Рср)2 * Вi
проект 1	проект 2	проект 1	проект 2	проект 1	проект 2
		0,05	-3,0	-2,0	-13,6	-15,0	9,25	11,25
		0,20	7,0	8.0	-3,6	-5,0	2,59	5,0
		0,50	11,0	14,0	0,4	1,0	0,08	0,5
		0,20	14,0	16,0	3,4	3,0	2,31	1,8
		0,05	21,0	26,0	10,4	13,0	5,41	8,45
Итого		1,0					19.64	27,0
Ожидаемая ВИД, % Рср=Σ(Вi * Pi)		10,6	13,0

Таблица 8.2. Оценка риска вариантов инвестиций

Показатели риска	Проект 1	Проект 2
Ожидаемая ВНД	10,6	13,0
Вариация	19.64	27,0
Стандартная девиация	4,43	5,2
Коэффициент вариации	0,42	0,40

По проекту 2 вариация равна 27,0 (значение сложно интерпретировать, так как единица измерения — процент в квадрате). Стандартная девиация при этом составила 5,2%, т. е. каждый сценарий в среднем будет иметь ВНД, отличающуюся от средней по данной инвестиционной альтернативе на ±5,2%. Эта величина и есть рисковая премия, учитываемая при формировании нормы дохода.

Пользуясь стандартной девиацией, нельзя сравнивать альтернативы с различной доходностью. Используют относительный показатель риска — коэффициент вариации, отношение стандартной девиации к ожидаемой ВНД. Для проекта 2 коэффициент вариации составит 0,4. Это меньше, чем для проекта 1.

Вывод: при оценке абсолютного риска проект 2 кажется более рискованным (самое высокое значение стандартной девиации), но если учесть относительный риск, то более рискованным окажется проект 1 (наибольшее значение коэффициента вариации).

Одной из разновидностей статистического метода оценки риска является «бета-анализ», который применяется для расчета величины риска портфельных инвестиций. Суть его сводится к выявлению устойчивости доходов данного инвестиционного проекта (вида ценных бумаг) относительно доходов по среднему показателю хорошо диверсифицированной инвестиционной программы (портфеля ценных бумаг):

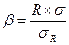, (8.4)

где R — корреляция между доходностью i-ro проекта (отдельного вида ценных бумаг) и средним уровнем доходности программы (портфеля ценных бумаг) в целом;

σ_i— стандартная девиация (среднее квадратичное отклонение) доходности по i-му инвестиционному проекту;

σ_R — стандартная девиация доходности инвестиционной программы (рынка ценных бумаг) в целом.

 

Используя значения β-коэффициента, можно оценивать уровень риска:

Значениеβ-коэффициента	Уровень риска
β= 1	Средний
β> 1	Высокий
β<1	Низкий

Величину риска можно уменьшить, изменяя набор проектов в инвестиционной программе предприятия, т. е. выбирая проекты с разным удельным весом инвестиций в общей программе.

Пример 8.2. Оценка риска инвестиционной программы предприятия с помощью «бета-анализа»

Программа состоит из четырех проектов, с конкретными значениями 3-коэффициентов, стоимость которых занимает определенную долю в инвестиционной программе (табл. 8.3). Для определения риска инвестиционной программы рассчитаем ее (3-коэффициент.

Таблица 8.3. Расчет β -коэффициентов

Проект	Доля инвестиций в программе, %	β	Расчет взвешенной р по инвестиционной программе
вариант 1	вариант 2	вариант 1	вариант 2
				5 (гр. 2х гр. 4)	6 (гр.3 х гр. 4)
А			0,9	0,225	0,225
Б			1,6	0,320	0,160
С			1,0	0,300	0,300
Д			0,7	0,175	0,245
Инвестиционная программа				1,020	0,93

Вывод: общий β по программе (вариант 1) равен 1,02. Если предприятие стремится снизить риск, то необходимо формировать инвестиционную программу так, чтобы па проект с меньшим значением 3 приходилась бы большая доля инвестиций. Так, если бы проект Д занимал 35% в стоимости программы, а проект Б — 10% (вариант 2 в табл. 8.3), то значение β по программе в целом составило бы 0,93, что свидетельствует об уменьшении риска.

При использовании «бета-анализа» норма дохода по инвестиционному проекту может быть рассчитана по следующей формуле:

Е_i = E_min + (P_ср – E_min) * β, (8.5)

где E_i — норма дохода по инвестиционному проекту с учетом риска;

Е_min — норма дохода по безрисковым инвестициям;

Р_cp — средняя норма дохода на инвестиционном рынке (аналогичных

проектов);

β — коэффициент, характеризующий уровень риска.

Вышеприведенная формула, определяющая взаимосвязь уровня риска и необходимой нормы дохода, называется ценовой моделью капитальных активов, САРМ (capital asset pricing model).

Недостаток статистического метода оценки риска заключается в необходимости большого массива исходных данных для расчета, который трудно получить. Поэтому на практике при оценке рисковой премии часто используют экспертный метод.

Содержание экспертного метода состоит в обработке мнений специалистов о величине рисковой премии в целом по проекту или по отдельным наиболее вероятным, с их точки зрения, видам рисков.

Возможно использование экспертного метода для оценки при поэлементном расчете рисковой премии (по видам рисков). Одна из классификаций факторов и размеров рисковой премии приведена в табл. 8.4.

В таблице в основном отражены риски, связанные с разработкой новой техники. Однако в ней присутствуют и виды рисков, не имеющие статистической закономерности проявления и, следовательно, не поддающиеся прогнозированию. Такие риски не следует учитывать при формировании нормы дохода. Методы их учета в инвестиционном проектировании рассмотрены в п. 8.4.4.

Экспертный метод широко используют для определения агрегированной рисковой премии (без разделения ее по видам рисков). При этом необходимо учитывать целевую направленность инвестиций, новизну и сложность применяемого оборудования. Для установления примерных размеров рисковой премии можно воспользоваться материалами исследования ряда американских промышленных компаний, дифференцирующими норму дохода в зависимости от класса инвестиций (табл. 8.5). Учитывая, что уровень минимально приемлемой (безрисковой) нормы дохода за рубежом составляет приблизительно 5% (ориентир — доходность 30-летнего государственного займа правительства США), можно определить размер рисковой премии по перечисленным классам инвестиций, вычитая из соответствующего значения нормы дохода величину безрисковой составляющей.

Графически изменение рисковой премии показано на рис. 8.5.

Таблица 8.4. Ориентировочная величина рисковой премии в зависимости л от вида риска

Факторы и виды риска	Прирост премииза риск, %
1.Необходимость проведения НИОКР (с заранее неизвестными результатами) силами специализированных научно-исследо-1 вательских и (или) проектных организаций:
■ продолжительность НИОКР менее 1 года	3-6
■ продолжительность НИОКР свыше 1 года:
> НИОКР выполняется силами одной специализированной организации	7-15
> НИОКР имеет комплексный характер и выполняется силами нескольких специализированных организаций	11-20
2. Характеристика применяемой технологии:
■ традиционная
■ новая, требующая применения ресурсов, имеющихся на свободном рынке	2-4
■ новая, требующая в отличие от существующей применения монополизированных ресурсов	5-10
■ новая, исключающая в отличие от существующей применение монополизированных ресурсов	1-3
3. Неопределенность объемов спроса и цен на производимую продукцию:
■ существующую	0-5
■ новую	5-10
4. Нестабильность (цикличность) спроса на продукцию	0-3
5. Неопределенность внешней среды при реализации проекта (горно-геологические, климатические и иные природные условия, агрессивность внешней среды и т. п.)	0-5
6. Неопределенность процесса освоения применяемой техники и технологии	0-3

Поскольку приведенная дифференциация рисковой премии отражает лишь качественный уровень применяемой в проектах техники и технологии, ее можно использовать и для российских условий.

Иностранные инвесторы стремятся в величине рисковой премии учесть страновый риск, при этом для России рекомендуется повышать безрисковую норму дохода в 2 раза. Для зарубежных стран такой риск определяется на основе специализированных рейтингов

Таблица 8.5. Определение величины рисковой премии в зависимости от класса инвестиций

Класс инвестиций	Норма дохода, %	Размер рисковой премии, %
		3(гр.2 —5%)
1. Вложения с целью сохранения позиций на рынке (в повышение качества продукции, рекламу)
2. Инвестиции на обновление основных фондов
3. Инвестиции с целью экономии текущих затрат (на базе новых технологических решений)
4. Вложения с целью увеличения доходов (для проектов, направленных на расширение производства на новой технологической основе на стабильном рынке)
5. Венчурные инвестиции (в инновационные проекты

фирмы BERI (Германия), Ассоциации швейцарских банков, корпорации Ernst & Young.

Недостаток экспертного метода — субъективность, связанная с влиянием на оценку индивидуальных особенностей эксперта. Однако, несмотря на несовершенство данного метода оценки риска, отказаться от его применения в современных российских условиях нельзя, так как он прост и нагляден в использовании.

 

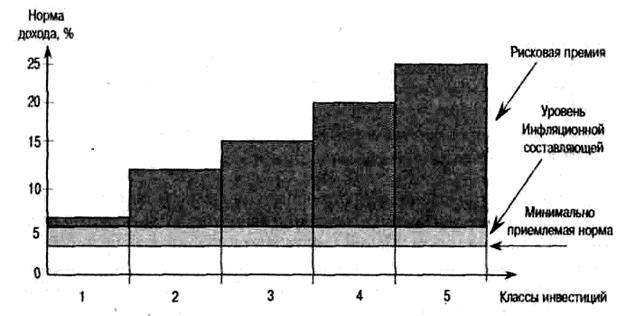
Рис. 8.5. Зависимость рисковой премии от класса инвестиций

⇐ Предыдущая27282930313233343536Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: