 |
Свойства эвольвентного зацепления
|
|
|
|
Рис. 5.3. зацепление зубьев с эвольвентными профилями.
Если профили зубьев двух колёс, очерченные эвольвентами 
(рис. 5.3), касаются в точке К, то общая нормаль n-n в точке контакта профилей будет касательной к обеим основным окружностям. При вращении колёс точка касания профилей переместится в 
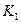, но общая нормаль по-прежнему будет касаться основных окружностей, т.е. её положение останется неизменным. Неизменным останется и положение полюса зацепления Р на межосевой линии, и, следовательно, зубья с эвольвентными профилями будут сопряжёнными. При вращении колёс точка контакта профилей зубьев всегда находится на прямой 
(рис.5.3), являющейся общей нормалью к профилям.
При изменении межосевого расстояния 
линия зацепления изменяет своё положение, изменяется угол зацепления , но сопряжённость зубьев и величина передаточного отношения не нарушаются. Из формулы и подобия 
и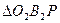 
следует
,
то есть передаточное отношение зубчатых колес равно обратному отношению радиусов основных окружностей.
С увеличением радиуса основной окружности одного из колёс до бесконечности будет уменьшаться кривизна эвольвенты, пока эвольвента не превратится в прямую.
В пределе получится зацепление рейки (колесо с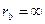 
) с зубьями прямолинейного профиля и колеса эвольвентным профилем зубьев. Следовательно, эвольвентныйм профиль зуба колеса является также сопряжённым с прямолинейным профилем рейки. Приближение или удаление рейки от оси колеса не нарушает сопряжённости профилей зубьев, изменяется лишь положение начальной прямой на рейке.
Эвольвентные передачи обладают рядом преимуществ:
а) возможность изменения в некоторых пределах межосевого расстояния без нарушения сопряжённости профилей;
|
|
|
б) зацепление зубчатого колеса с любым другим при одинаковых параметрах зацепления;
в) возможность осуществления передачи без мёртвого хода;
г) сравнительно простое изготовление колёс.
5.4. Элементы эвольвентного зубчатого колеса
Рис. 5.4. Элементы эвольвентного зубчатого зацепления.
Дуга начальной окружности, вмещающая один зуб (без впадин) носит название толщины зуба (обозначается S), а дуга начальной окружности вмещающая впадину (расстояние между соседними зубьями (
)). Дуга начальной окружности, состоящая из одной толщины зуба и одной ширины впадины, называется шагом зацепления по начальной окружности и обозначается t:
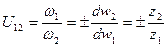, (5.7)
где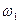 
и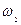 
- угловые скорости колёс 1 и 2;
и 
- диаметры начальных окружностей, 
и - числа их зубьев.
Длины начальных окружностей колёс 1 и 2:
и 
(5.8)
Шаг зацепляется по начальной окружности
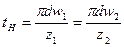(5.9)
Отсюда видно, что шаг зацепления всегда выражается через радиус или через диаметр окружности несоизмеримым числом, так как в правую часть входит трансцендентное число 
. Это затрудняет подбор размеров зубчатых колёс при проектировании колёс и практическое их измерение. Поэтому, для определения основных размеров зубчатых колёс в качестве основной единицы принят некоторый параметр, называемый модулем зацепления. Модуль зацепления измеряется в миллиметрах и обозначается буквой m.
(5.10)
Модули, полученные из расчёта должны округляться до стандартных. Их два ряда, первый предпочтительный:
1-ый……………..1,25; 1,5; 2; 2,5; 3; 4; 5; 8; 10; 12; 15;……….
2-ой………………………………3,5; 4,5; 5,5; 7; 9; 11;………..
Окружность зубчатого колеса, для которого модуль получается стандартным, называется длительный. В этом случае длительная окружность совпадает с начальной окружностью. Размеры зубчатых колёс определяются из следующих соотношений:
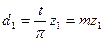(5.11)
(5.12)
Высота 
головки зуба и высота 
ножки зуба обычно принимается равными 
и 
. Больший размер ножки по сравнению с головкой зуба обеспечивает зазор между головкой зуба и впадиной. Тогда диаметры выступов:
|
|
|
(5.13)
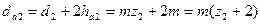(5.14)
Диаметры впадин:
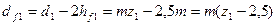(5.15)
(5.16)
|
|
|
