 |
Определение основных размеров кулачковых механизмов
|
|
|
|
Основные размеры кулачковых механизмов определяются из кинематических, динамических и конструктивных условий. Кинематические условия определяются тем, что механизм должен воспроизводить заданный закон движения. Динамические условия весьма разнообразны, но основной в том, чтобы механизм имел высокий КПД. Конструктивные требования определяются из условия достаточной прочности отдельных деталей механизма – сопротивляемости износу соприкасающихся кинематических пар. Проектируемый механизм должен обладать наименьшими габаритами.
Рис.6.4. К силовому анализу кулачкового механизма с поступательно-движущемся толкателем.
Рис.6.5. К исследованию угла давления в кулачковом механизме
На рис. 6.4 показан кулачковый механизм с толкателем 2, оканчивающийся остриём 
. Если пренебречь трением в высшей кинематической паре, то сила 
, действующая на толкатель 2 со стороны кулачка 1. Угол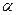 
, образованный нормалью n-n к профилю кулачка 1. Угол 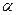, образованный нормалью n-n и направлением движения толкателя 2, является углом давления а угол 
, равный 
, является углом передачи. Если рассмотреть равновесие толкателя 2 (рис. 10.5) и подвести все силы к точке , то толкатель будет находиться под действием движущей силы 
, приведённой силы сопротивления T, учитывающей полезные сопротивления, силу пружины, силы инерции, и приведённой силы трения F. Из уравнения равновесия сил, действующих на толкатель 2, имеем
Приведённая сила трения T равна
,
Где 
- коэффициент трения в направляющих;
-длина направляющих;
- вылет толкателя.
Тогда из уравнения равновесия сил получаем, что сила трения равна
(6.5)
Мгновенный коэффициент полезного действия 
механизма без учёта трения в высшей паре и подшипнике вала кулачка можно определить по формуле
|
|
|
(6.6)
Величина вылета k толкателя равна (рис.6.5)
,
Где b- постоянное расстояние от точки N опоры толкателя 2 до оси А вращения кулачка;
-наименьший радиус вектор кулачка 1
-перемещение толкателя 2.
Имеем 
Из рис. 6.5 получаем
(6.7)
так как
(6.8)
Из уравнения (6.7) получаем
Тогда коэффициент полезного действия будет равен
(6.9)
Из равенства (6.9) следует, что коэффициент полезного действия уменьшается с увеличением угла давления 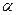. Кулачковый механизм может заклиниться, если сила 
(рис.6.5) будет 
. Заклинивание произойдёт, если коэффициент полезного действия будет равен нулю. Тогда из равенства (6.9) получим
- критический угол, при котором возникает заклинивание механизма, и 
- соответствующий этому углу аналог скорости.
Тогда для критического угла давления будем иметь:
(6.10)
Из равенства (6.10) следует, что критический угол давления уменьшается с увеличением расстояния в т.е. с увеличением габаритов механизма. Приближённо можно считать, что значение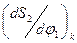 
аналога скоростей, соответствующее критическому углу , равно максимальному значению этого аналога, т.е.
Тогда, если заданы размеры механизма и закон движения толкателя, можно определить значение критического угла давления . Необходимо иметь в виду, что заклинивание механизма обычно имеет место только на фазе подъёма, соответствующей преодолению полезных сопротивлений, силы инерции толкателя и силы пружины, т.е. когда преодолевается некоторая приведённая сила сопротивления T (рис. 6.5). На фазе опускания явление заклинивания не возникает.
Для устранения возможности заклинивания механизма при проектировании ставят условие, чтобы угол давления 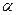во всех положениях механизма был меньше критического угла . Если максимально допустимый угол давления обозначить через 
, то этот угол должен всегда удовлетворять условию
|
|
|
(6.11)
на практике угол давления для кулачковых механизмов с поступательно движущимся толкателем принимаются
Для кулачковых механизмов с вращающимся коромыслом, в котором заклинивание является менее возможным, максимальный угол давления 
При проектировании кулачковых можно примять в расчётах не угол давления 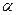, а угол передачи . Этот угол должен удовлетворять условиям
, где 
6.4. Определение угла давления 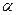через основные параметры кулачкового механизма
Угол давления 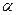может быть выражен через основные параметры кулачкового механизма. Для этого рассмотрим кулачковый механизм (рис.6.4) с поступательно движущимся толкателем 2. Проводим в т. нормаль 
и находим мгновенный центр вращения 
в относительном движении звеньев 1 и 2. Из 
имеем:
(6.12)
Согласно равенству (6.8) 
, 
, где - кратчайшее расстояние от оси А кулачка до оси толкателя, 
, где 
- минимальный радиус вектор кулачка и 
, где, заданное его законом движения 
.
Подставляя указанные параметры в равенство (6.12), получаем
(6.13)
Знак “+” у кратчайшего расстояния l соответствует левому от оси А его расположению, знак "-" - правому (6.4) при условии, что толкатель движется вверх, а кулачок вращается против часовой стрелки.
Из равенства (6.13) следует, что при выбранном законе движения и размере габариты кулачка определяются радиусом 
, мы получаем меньшие углы давления 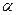, но большие габариты кулачкового механизма.
И наоборот, если уменьшить , то возрастают углы давления 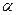и уменьшается коэффициент полезного действия механизма. Если в механизме (рис.6.5) ось движения толкателя проходит через ось вращения кулачка и 
, то равенство (6.13) примет вид
(6.14)
|
|
|
