Ограничения применимости критерия

1. В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было два значения, но во второй тогда не менее пяти.

2. В выборочных данных не должно быть совпадающих значений (все числа - разные) или таких совпадений должно быть очень мало.

Использование критерия

Для применения U-критерия Манна-Уитни нужно произвести следующие операции.

1. Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным: N = n₁ + n₂, где n₁ — количество единиц в первой выборке, а n₂ — количество единиц во второй выборке.

2. Разделить единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок. Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки. Определить большую из двух ранговых сумм (T_x), соответствующую выборке с n_x единиц.

3. Определить значение U-критерия Манна-Уитни по формуле: .

4. По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных n₁ и n₂. Если полученное значение U меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение U.

5. При справедливости нулевой гипотезы критерий имеет матожидание 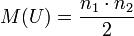и дисперсию 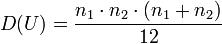и при достаточно большом объёме выборочных данных (n₁ > 19,n₂ > 19) распределён практически нормально.

3. Критерий Т Вилкоксона для сопоставления двух показателей испытуемых.

Алгоритм применения

1. Составить список испытуемых.

2. Вычислить разность между индивидуальными значениями во 2-м и 1-м замерах ("после" - "до"). Определить, что будет считаться "типичным" сдвигом, и сформулировать гипотезу.

3. Найти абсолютные величины разностей.

4. Проранжировать абсолютные величины разностей, начиная с меньшего значения.

5. Отметить ранги, соответствующие сдвигам в "нетипичном" направлении, подсчитать сумму этих рангов .

6. Определить критические значения для данного (по таблице прил. 10). Если , то сдвиг в "типичную" сторону по интенсивности достоверно преобладает.

7. Критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых.

12 участников тренинга партнерского общения дважды ("до" и "после") оценивали у себя уровень владения аргументацией. Получены данные по 10-балльной шкале.

 

8.

9.

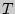попадает в зону неопределенности, следовательно, отвергается.

4. G – КРИТЕРИЙ ЗНАКОВ

Назначение

G-критерий знаков применяется при выяснении направ­ления сдвига при переходе от первого измерения ко второму на одной и той же выборке испытуемых.

Ограничения

Количество измерений в каждом из двух замеров не менее 5 и не более 300, т.е. 5 ≤ n1 ≤ 300 и 5 ≤ n2 ≤ 300.

Алгоритм использования

 

1. проверить выполнение ограничений;

2. занести данные измерений в таблицу:

Испытуемые				… n
Значения «до воздействия»	.	.	.	….
Значения «после воздействия»	.	.	.	….
Сдвиг («после» - «до»)	.	.	.	….

Сдвиг количественно не подсчитывается, ставится просто, знак разности («+» или «-»), когда из значения «после воздействия» вычитается значение «до воздействия». Если разность эта равна нулю, то в таблице пишут нуль.

3. подсчитать количество нулевых реакций n0 и вычесть их из объема вы­борки п. Новый объем выборки найти по формуле: n = n - n0;

4. определить, каких сдвигов больше: положительных или отрицатель­ных. Считать «типичными» те сдвиги, которых больше. А «нетипичны­ми» - те, которых меньше;

5. сформулировать гипотезы:

Но: Сдвиг в типичную сторону является случайным;

H1: Сдвиг в типичную сторону является неслучайным.

6. подсчитать количество «нетипичных» сдвигов и найти эмпирическое значение G-критерия: G эмп. равно количеству «нетипичных» сдвигов;

7. по таблице 1 приложения по значению n найти G кр. (p ≤ 0,05) и G кр. (p ≤ 0,01), изобразить все полученные значения на оси значимости.

зона значимости зона неопределенности зона не значимости

G кр. (p ≤ 0,01) G кр. (p ≤ 0,05)

Если G эмп. ≤ G кр. на некотором уровне значимости, то H0 отвергается, а H1 принимается на этом уровне значимости.

Если G эмп. › G кр. на некотором уровне значимости, то H0 принимается на том же уровне значимости. Чем меньше G эмп., тем более вероятно, что сдвиг в типичном направлении статистически достоверен.

 

⇐ Предыдущая35363738394041424344Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: