 |
Статистические критерии различий. Параметрические и непараметрические критерии.
|
|
|
|
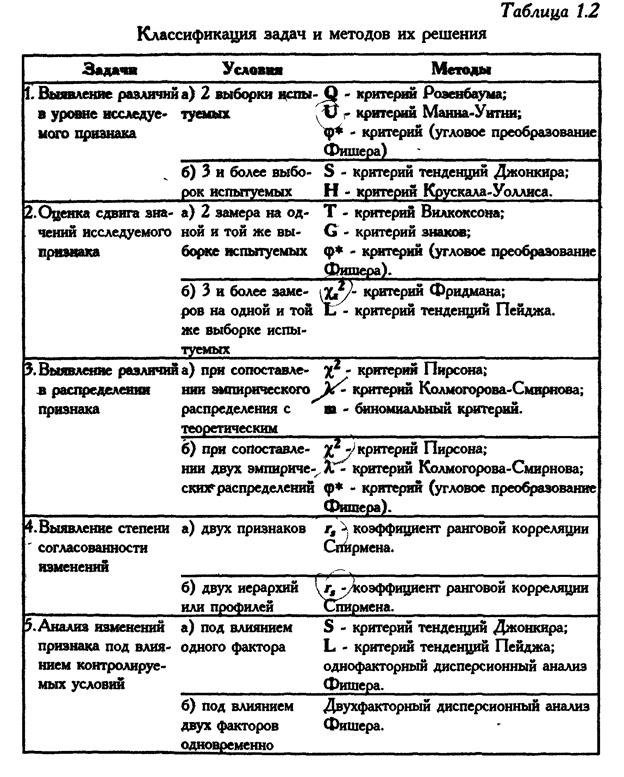
Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.
Статистические критерии подразделяются на следующие категории:
* Критерии значимости. Проверка на значимость предполагает проверку гипотезы о численных значениях известного закона распределения: H_0: quad a=a_0 — нулевая гипотеза. H_1: quad a>a_0 quad (a или a eq a_0 — конкурирующая гипотеза.
* Критерии согласия. Проверка на согласие подразумевает проверку факта о том, что исследуемая случайная величина подчиняется предполагаемому закону. Критерии согласия можно также воспринимать, как критерии значимости.
* Критерии на однородность. При проверке на однородность случайные величины исследуются на факт взаимного соответствия их законов распределения (подчиняются ли эти величины одному и тому же закону). Используются в факторном (дисперсионном) анализе для определения наличия зависимостей.
Непараметрические критерии
Группа статистических критериев, которые не включают в расчёт парметры вероятностного распределения и основаны на оперировании частотами или рангами.
* Q-критерий Розенбаума
* U-критерий Манна-Уитни
* Критерий Колмогорова
* Критерий Уилкоксона
Параметрические критерии
Группа статистических критериев, которые включают в расчет параметры вероятностного распределения признака (средние и дисперсии).
* t-критерий Стьюдента
|
|
|
* Критерий Колмогорова
* Критерий отношения правдоподобия
* Критерий Пирсона
Параметрические критерии:
1. Критерий Фишера (F-критерий, φ*-критерий, критерий наименьшей значимой разности) — апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в установке дисперсионного анализа.
2. t-критерий Стьюдента - общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
Алгоритм применения 
-критерия Стьюдента для сравнения оценки средних величин двух выборок
1. Записать вариационный ряд результатов X экспериментальной группы.
2. Записать вариационный ряд результатов Y контрольной группы.
3. Найти выборочные средние двух выборок x и y.
4. Найти выборочные дисперси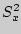и 
и 
.
5. Вычислить эмпирическое значение критической статистики 
Определить по таблице критическое значение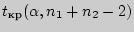 
для соответствующего уровня значимости 
и данного числа степеней свободы 
.
Если 
, то различия между средними значениями экспериментальной и контрольной групп существенны на данном уровне значимости.
Особенности использования t-критерия Стьюдента. Наиболее часто t -критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящая из разных пациентов, количество которых в группах может быть различно.
Во втором же случае используется так называемый парный t-критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.
|
|
|
|
|
|
