 |
Интерактивные технологии и инновационные методы, используемые в образовательном процессе
|
|
|
|
УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС
учебной дисциплины «Количественные методы в менеджменте»
цикла Б2 Профессиональный цикл
направления 080200 «Менеджмент»
профиль 08020011 «Финансовый менеджмент»
| Составитель: к.ф.-м.н., ст. преп. | Д.Н.Карасев |
Ростов-на-Дону
Министерство образования и науки Российской Федерации
Ростовский государственный экономический университет (РИНХ)
| Утверждаю |
| Проректор по учебно-методической работе |
| Маслова Н.П. _______ |
| «___» _______ 2011г. |
Рабочая программа дисциплины (модуля)
Количественные методы в менеджменте _________________
(указывается наименование дисциплины (модуля))
Направление подготовки
080200 «Менеджмент» _
(указывается код и наименование направления подготовки)
Профиль: 08020011 «Финансовый менеджмент»
Квалификация (степень)
____Бакалавр___
Ростов-на-Дону
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ (РИНХ)
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
ДИСЦИПЛИНЫ
Б2.ДВ2 «Количественные методы в менеджменте»
(индекс дисциплины по учебному плану) (наименование дисциплины)
НАПРАВЛЕНИЕ
080200 «Менеджмент»
(код) (наименование)
ПРОФИЛЬ
08020011 «Финансовый менеджмент»
(код) (наименование)
| ФАКУЛЬТЕТ | Национальной и мировой экономики | |
| КАФЕДРА | Менеджмент |
(код) (наименование)
| ОБЩИЙ ОБЪЕМ* | ФГОС | Уч.план | Очная форма | Заочная форма | |
| работы студента в час. | 4г 00м | 5г 00м | 3г 06м | ||
| Всего аудиторных занятий, час, в том числе: | |||||
| - лекций, по семестрам | |||||
| 3 сем | 2 курс | 2 курс | |||
| - лабораторные работы (или занятия по подгруппам), по семестрам | |||||
| - практические занятия, по семестрам | |||||
| 3 сем | 2 курс | 2 курс | |||
| В интерактивной форме, час | |||||
| Всего самостоятельной работы, час, в том числе: | |||||
| - контрольные работы по семестрам | 2 курс | ||||
| - курсовые работы по семестрам | |||||
| - курсовые проекты по семестрам | |||||
| - др. виды работы по семестрам | |||||
| Зачеты, по семестрам | |||||
| Экзамены, по семестрам | 2 курс | 2 курс | |||
| Всего ЗЕТ по учебному плану | 3,5 |
* Объем часов по всем видам работ переносится из учебного плана.
|
|
|
ОСНОВАНИЕ
Рабочий учебный план подготовки бакалавра по профессионально-образовательной программе направление 080200 «Менеджмент», профиль 08020011 "Финансовый менеджмент" одобрен Ученым советом вуза 28.02.2011 г. протокол № 6
Нормативные документы и реквизиты (ФГОС, ПрООП, Учебный план, и др.)
| АВТОР к.ф.-м.н., старший преподаватель | Карасев Д.Н. | ||
| (ученая степень, звание, должность) | (подпись) | (Ф.И.О.) | (дата) |
ОБСУЖДАЛАСЬ И СОГЛАСОВАНА
| Кафедрой Менеджмента | Димитриади Н.А. | ||
| (наименование) | (подпись) | (Ф.И.О.) | (дата) |
| Методическим советом направления/ специальности | Алифанова Е.Н. |
| Учебно-методическим управлением | Иванова Е.А. |
Экспертное заключение
Методического Совета направления подготовки 080200 «Менеджмент», квалификация (степень) «бакалавр» о рабочей программе по дисциплине «Количественные методы в менеджменте» по профилям подготовки 08020011 «Финансовый менеджмент».
Рассмотрев структуру, содержание и качество оформления рабочей программы по дисциплине «Количественные методы в менеджменте» учебного плана, методический совет отмечает:
- рабочая программа соответствует государственному образовательному стандарту высшего профессионального образования по направлению подготовки 080200 «Менеджмент», квалификация (степень) «бакалавр» в части выполнения требований, предъявляемых к уровню профессиональной квалификации выпускников, их знаний, умений и навыков по соответствующему циклу дисциплин и по самой дисциплине;
|
|
|
- рабочая программа по данной дисциплине составлена с учетом обоснованности междисциплинарной логики и соотношения объемов ее основных разделов;
- в рабочей программе согласован бюджет времени, отводимый на различные виды аудиторных занятий (лекционных, семинарских) с бюджетом времени на различные формы самостоятельной работы (выполнение индивидуальных творческих заданий,усвоение текущего учебного материала, выполнение домашних заданий, подготовка к практическим занятиям);
- в рабочей программе предусмотрены полнота и достаточность информационно-методического обеспечения учебных занятий и самостоятельной работы.
Совет рекомендует преподавателям, осуществляющим чтение курса и проведение практических занятий, в зависимости от конкретной обстановки, совершенствовать рабочую программу с учетом контингента студентов и изменения требований.
На основании вышеизложенного совет предлагает утвердить рабочую программу по учебной дисциплине «Количественные методы в менеджменте», представленной на экспертизу.
Подписи:
Подписи:
Председатель совета Е.Н. Алифанова
Г.П. Чубарова
Е.В. Добролежа
Т.Ф. Романова
О.Г. Семенюта
В.Ю. Наливайский
В.Ю. Барашьян
1. Цели и задачи дисциплины
1.1. Цель, задачи дисциплины, ее место в подготовке бакалавра, (с учетом требований ФГОС)
| Дисциплина «Количественные методы в менеджменте» является дисциплиной по выбору цикла дисциплин ФГОС ВПО по направлению «Менеджмент». Дисциплина является общим и теоретическим основанием для решения научных и прикладных задач в области менеджмента для бакалавров по направлению «Менеджмент», профиль "Финансовый менеджмент". Цели: оснастить студентов математическим аппаратом, необходимым для применения математических методов в практической деятельности и в исследованиях в области менеджмента. Задачи:теоретическое освоение студентами современных концепций и моделей математики; приобретение практических навыков применения аппарата математики при решении менеджерских задач. |
|
|
|
1.2.Требования к уровню усвоения дисциплины
| Студент должен знать: основные количественные методы, применяемые в менеджменте. |
| Студент должен уметь: применять основные количественные методы при решении различных управленческих задач, правильно оценивать возможность и целесообразность применения количественных методов при решении конкретных управленческих задач. |
| Студент должен иметь представление: об области применения количественных методов в менеджменте и уровне их эффективности. |
| У студента должны быть сформированы следующие общекультурные компетенции (ОК) и профессиональные компетенции (ПК): ОК-15 владеть методами количественного анализа и моделирования, теоретического и экспериментального исследования, ОК-16 пониманием роли и значения информации и информационных технологий в развитии современного общества и экономических знаний, ОК-17 владеть основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией, ОК-18 способностью работать с информацией в глобальных компьютерных сетях и корпоративных информационных системах. |
1.3.Связь с другими дисциплинами Учебного плана
| Перечень действующих и предшествующих дисциплин | Перечень последующих дисциплин, видов работ |
| Линейная алгебра Математический анализ Маркетинг | Управление проектами Стратегический менеджмент |
2. Содержание дисциплины, способы и методы учебной деятельности преподавателя
Методы обучения – система последовательных, взаимосвязанных действий, обеспечивающих усвоение содержания образования, развитие способностей студентов, овладение ими средствами самообразования и самообучения; обеспечивают цель обучения, способ усвоения и характер взаимодействия преподавателя и студента; направлены на приобретение знаний, формирование умений, навыков, их закрепление и контроль.
|
|
|
| Монологический (изложение теоретического материала в форме монолога) | М |
| Показательный (изложение материала с приемами показа) | П |
| Диалогический (изложение материала в форме беседы с вопросами и ответами) | Д |
| Эвристический (частично поисковый) (под руководством преподавателя студенты рассуждают, решают возникающие вопросы, анализируют, обобщают, делают выводы и решают поставленную задачу) | Э |
| Проблемное изложение (преподаватель ставит проблему и раскрывает доказательно пути ее решения) | ПБ |
| Исследовательский (студенты самостоятельно добывают знания в процессе разрешения проблемы, сравнивая различные варианты ее решения) | И |
| Программированный (организация аудиторной и самостоятельной работы студентов осуществляется в индивидуальном темпе и под контролем специальных технических средств) | ПГ |
| Другой метод, используемый преподавателем (формируется самостоятельно), при этом в п.п. 2.1.-2.4. дается его наименование, необходимые пояснения |
Приведенные в таблице сокращения обозначения педагогических методов используются составителем Рабочей программы для заполнения п.п. 2.1., 2.2. и 2.3. в столбце «Методы».
2.1. Аудиторные занятия (лекции, лабораторные, практические, семинарские)
| Неделя | Кол. час | в том числе в интерактивной форме, час. | Вид занятия, модуль, тема и краткое содержание | Методы | Реализуемые компетенции |
| Очная форма обучения | |||||
| Третий семестр | |||||
| Лекции | |||||
| 1-8 | Модуль 1 «Элементы теории игр» | М,Д,И,Э | ОК-15 ОК-16 | ||
| 1-2 | - | Тема. «Введение в теорию игр». Постановка задачи теории игр. Основные понятия и базовые принципы теории игр. Классификация игр. | М,Д,И | ОК-15 | |
| 3-4 | Тема. «Конечные парные игры. Игры, разрешимые в чистых стратегиях». Верхняя и нижняя цена игры. Седловая точка. Игры, разрешимые в чистых стратегиях | М | ОК-16 | ||
| 5-6 | - | Тема. «Игры, неразрешимые в чистых стратегиях. Смешанные стратегии» Разрешимость игры в смешанных стратегиях. Понятие оптимального решения. Алгоритм решения игры в смешанных стратегиях. Графическая интерпретация игры 2х2. | М, Д | ОК-15 ОК-16 | |
| 7-8 | Тема. «Оптимальное решение в теории игр. Типы устойчивости» Понятие оптимального решения. Типы устойчивости. Типовая менеджерская задача по определению типов равновесий и проблемы менеджмента | М,Д | ОК-15 | ||
| 9-18 | Модуль 2 «Элементы теории графов» | М,Д,И,Э | ОК-17 ОК-18 | ||
| 9-10 | Тема. «Понятие графа». Понятие графа. Основные характеристики графа. Классификация графов. Операции над графами. Матрицы смежности. | М,Д | ОК-18 | ||
| 11-12 | - | Тема. «Изоморфизм графов». Понятие изоморфизма графов. Маршрут, цепь, цикл, контур, путь. | М,Д | ОК-17 | |
| 13-14 | Тема. «Оптимизация на графах» Задача о кратчайшем пути. Задача о максимальном потоке. Календарно-сетевое планирование. Алгоритмы решения задач и области их применения. | И, Э,Д | ОК-18 ОК-17 | ||
| 15-16 | - | Тема. «Сети Петри» Понятие сетей Петри. Простые сети Петри. Цветные сети Петри. | Э,И,Д | ОК-18 ОК-17 | |
| 17-18 | Тема. «Анализ сети Петри» Анализ сети Петри. Типовая менеджерская задача по сетям Петри | М,Д | ОК-18 | ||
| Очная форма обучения | |||||
| Третий семестр | |||||
| Практические занятия | |||||
| 1-8 | Модуль 1 «Элементы теории игр» | М,Д,И,Э | ОК-15 | ||
| - | Тема. «Введение в теорию игр». Постановка задачи теории игр. Основные понятия и базовые принципы теории игр. | М,Д,И | ОК-15 | ||
| Тема "Классификация игр" Классификация игр | М, Д | ОК-15 | |||
| Тема. «Конечные парные игры. Игры, разрешимые в чистых стратегиях». Верхняя и нижняя цена игры. Седловая точка. | М | ОК-15 | |||
| Тема " Разрешимость в чистых стратегиях" Игры, разрешимые в чистых стратегиях | М, Д | ОК-15 | |||
| - | Тема. «Игры, неразрешимые в чистых стратегиях. Смешанные стратегии» Разрешимость игры в смешанных стратегиях. Понятие оптимального решения. Алгоритм решения игры в смешанных стратегиях. | М, Д | ОК-15 | ||
| Тема "Графическая интерпретация игры 2х2" Алгоритм решения игры 2х2 через графическую интерпретацию. | М, Д | ОК-15 | |||
| Тема. «Оптимальное решение в теории игр. Типы устойчивости» Понятие оптимального решения. Типы устойчивости. | М,Д | ОК-15 | |||
| Тема "Типы устойчивости в теории игр" Типовая менеджерская задача по определению типов равновесий и проблемы менеджмента | М, Д | ОК-15 | |||
| 9-18 | Модуль 2 «Элементы теории графов» | М,Д,И,Э | ОК-15 | ||
| Тема. «Понятие графа». Понятие графа. Основные характеристики графа. Классификация графов | М,Д | ОК-15 | |||
| Тема "Понятие графа" Операции над графами. Матрицы смежности. | М,Д | ОК-15 | |||
| - | Тема. «Изоморфизм графов». Понятие изоморфизма графов. | М,Д | ОК-15 | ||
| Тема " Маршрут, цепь, цикл, контур, путь. " Понятия маршрута, цепь, цикл, контур, путь. | М,Д | ОК-15 | |||
| Тема. «Оптимизация на графах» Задача о кратчайшем пути. Задача о максимальном потоке. Календарно-сетевое планирование | И, Э,Д | ОК-15 | |||
| Тема "Оптимизация на графах" Алгоритмы решения задач и области их применения. | М,Д | ОК-15 | |||
| - | Тема. «Сети Петри» Понятие сетей Петри. Простые сети Петри. | Э,И,Д | ОК-15 | ||
| Тема "Сети Петри" Цветные сети Петри. | М,Д | ОК-15 | |||
| - | Тема. «Анализ сети Петри» Анализ сети Петри. | М,Д | ОК-15 | ||
| Тема "Анализ сети Петри" Типовая менеджерская задача по сетям Петри | М,Д | ОК-15 |
2.2.Аудиторные занятия (лекции, практические) - заочная форма обучения, срок обучения-5 лет
|
|
|
| Кол. час | Вид занятия, модуль, тема и краткое содержание | Методы | Реализуемые компетенции |
| Лекции | |||
| Тема. «Введение в теорию игр». Постановка задачи теории игр. Основные понятия и базовые принципы теории игр. Классификация игр. | М,Д | ОК-15 | |
| Тема. «Конечные парные игры. Игры, разрешимые в чистых стратегиях». Верхняя и нижняя цена игры. Седловая точка. Игры, разрешимые в чистых стратегиях | И, Э,Д | ОК-16 ОК-17 | |
| Практика | |||
| Тема. «Оптимизация на графах» Задача о кратчайшем пути. Задача о максимальном потоке. Календарно-сетевое планирование. Алгоритмы решения задач и области их применения. | Э,И,Д | ОК-15 ОК-18 | |
| Тема. «Игры, неразрешимые в чистых стратегиях. Смешанные стратегии» Разрешимость игры в смешанных стратегиях. Понятие оптимального решения. Алгоритм решения игры в смешанных стратегиях. Графическая интерпретация игры 2х2. | И, Э,Д | ОК-15 ПК-17 | |
| Тема. «Анализ сети Петри» Анализ сети Петри. | И, Э,Д | ОК-15 ПК-17 |
2.3. Аудиторные занятия (лекции, практические) - заочная форма обучения, срок обучения-3 года, 6 мес.
| Кол. час | Вид занятия, модуль, тема и краткое содержание | Методы | Реализуемые компетенции |
| Лекции | |||
| Тема. «Конечные парные игры. Игры, разрешимые в чистых стратегиях». Верхняя и нижняя цена игры. Седловая точка. Игры, разрешимые в чистых стратегиях. Игры, разрешимые в смешанных стратегиях. | И, Э,Д | ОК-16 ОК-17 | |
| Практика | |||
| Тема. «Оптимизация на графах» Задача о кратчайшем пути. Задача о максимальном потоке. Календарно-сетевое планирование. Алгоритмы решения задач и области их применения. | Э,И,Д | ОК-15 ОК-17 | |
| Тема. «Игры, неразрешимые в чистых стратегиях. Смешанные стратегии» Разрешимость игры в смешанных стратегиях. Понятие оптимального решения. Алгоритм решения игры в смешанных стратегиях. Графическая интерпретация игры 2х2. | И, Э,Д | ОК-15 ОК-18 |
2.4.Самостоятельная работа студента
| Неделя | Кол. Час | Темы, разделы, вынесенные на самостоятельную подготовку, вопросы к практическим и лабораторным занятиям; тематика рефератной работы, контрольных работ, рекомендации по использованию литературы и ЭВМ и др. | Реализуемые компетенции |
| Очная форма обучения | |||
| Третий семестр | |||
| 1-2 | Проблема многокритериального выбора. | ОК-15 | |
| 7-11 | Статистические методы в менеджменте. | ОК-16 | |
| 1-18 | Усвоение текущего материала | ОК-15 ОК-16 | |
| 1-18 | Темы и вопросы, определяемые преподавателем с учетом интересов студента. "Анализ сетей Петри" | ОК-17 | |
| Заочная форма обучения 5 лет | |||
| Проблема многокритериального выбора. | ОК-15 | ||
| Статистические методы в менеджменте. | ОК-16 | ||
| Постановка задачи теории игр. Основные понятия и базовые принципы теории игр. Классификация игр. | ОК-17 ОК-15 | ||
| Конечные парные игры. Игры, разрешимые в чистых стратегиях. | ОК-18 | ||
| Разрешимость игры в смешанных стратегиях. Понятие оптимального решения. Алгоритм решения игры в смешанных стратегиях. Графическая интерпретация игры 2х2. | ОК-15 ОК-16 ОК-17 | ||
| Оптимальное решение в теории игр. Типы устойчивости | ОК-15 | ||
| Понятие графа. Основные характеристики графа. Классификация графов. Операции над графами. Матрицы смежности. | ОК-15 ОК-18 | ||
| Изоморфизм графов. Маршрут, цепь, цикл, контур, путь. | ОК-15 | ||
| Задача о кратчайшем пути. Задача о максимальном потоке. Календарно-сетевое планирование. Алгоритмы решения задач и области их применения. | ОК-16 ОК-18 | ||
| Понятие сетей Петри. Простые сети Петри. Цветные сети Петри. | ОК-17 | ||
| Анализ сети Петри. Типовая менеджерская задача по сетям Петри | ОК-15 | ||
| Усвоение текущего материала | ОК-15 ОК-16 | ||
| Заочная форма обучения 3 года, 6 мес. | |||
| Проблема многокритериального выбора. | ОК-15 | ||
| Статистические методы в менеджменте. | ОК-16 | ||
| Постановка задачи теории игр. Основные понятия и базовые принципы теории игр. Классификация игр. | ОК-17 ОК-15 | ||
| Конечные парные игры. Игры, разрешимые в чистых стратегиях. | ОК-18 | ||
| Разрешимость игры в смешанных стратегиях. Понятие оптимального решения. Алгоритм решения игры в смешанных стратегиях. Графическая интерпретация игры 2х2. | ОК-15 ОК-16 ОК-17 | ||
| Оптимальное решение в теории игр. Типы устойчивости | ОК-15 | ||
| Понятие графа. Основные характеристики графа. Классификация графов. Операции над графами. Матрицы смежности. | ОК-15 ОК-18 | ||
| Изоморфизм графов. Маршрут, цепь, цикл, контур, путь. | ОК-15 | ||
| Задача о кратчайшем пути. Задача о максимальном потоке. Алгоритмы решения задач и области их применения. | ОК-16 ОК-18 | ||
| Календарно-сетевое планирование. | ОК-16 | ||
| Понятие сетей Петри. Простые сети Петри. Цветные сети Петри. | ОК-17 | ||
| Анализ сети Петри. Типовая менеджерская задача по сетям Петри | ОК-15 | ||
| Усвоение текущего материала | ОК-15 ОК-16 |
Интерактивные технологии и инновационные методы, используемые в образовательном процессе
Основаны на использовании современных достижений науки и информационных технологий. Направлены на повышение качества подготовки путем развития у студентов творческих способностей и самостоятельности (методы проблемного обучения, исследовательские методы, тренинговые формы, рейтинговые системы обучения и контроля знаний и др.). Нацелены на активизацию творческого потенциала и самостоятельности студентов и могут реализовываться на базе инновационных структур (научных лабораторий, центов, предприятий и организаций и др.).
| № | Наименование основных форм | Краткое описание и примеры, использования в модулях темах, место проведения | Часы |
| - | Применение электронных мультимедийных учебников и учебных пособий | Находятся в электронном читальном зале РГЭУ (РИНХ) | |
| - | Разбор конкретных ситуаций | Тема. «Конечные парные игры. Игры, разрешимые в чистых стратегиях» в модуле 1 на лекции; Тема. «Оптимальное решение в теории игр. Типы устойчивости» в модуле 1 на лекции; Тема. «Понятие графа» в модуле 2 на лекции; Тема. «Оптимизация на графах» в модуле 2 на лекции; Тема. «Конечные парные игры. Игры, разрешимые в чистых стратегиях» в модуле 1 на практике; Тема. «Оптимальное решение в теории игр. Типы устойчивости» в модуле 1 на практике; Тема. «Понятие графа» в модуле 2 на пректике; Тема. «Оптимизация на графах» в модуле 2 на практике. | |
| - | Ориентация содержания на лучшие отечественные аналоги образовательных программ | Содержание дисциплины ориентируется на образовательную программу Финансового университета при правительстве Российской Федерации |
3. Средства обучения
3.1.Информационно-методические
| № | Перечень основной и дополнительной литературы, методических разработок; с указанием наличия в библиотеке | |
| Основная литература: | ||
| 1. | Ерусалимский Я.М. Дискретная математика. М: ВШ,1999 | |
| 2. | Прикладные нечёткие системы../ Под ред. Т.Тэрано, К.Фсаи, М.Сугэно./М: Мир,1993 | |
| 3. | Воробьев Н.Н. Теория игр для экономистов и кибернетиков. M., 1985 | |
| 4. | Коханенко И.К. Элетронный Практикум по дисциплине Количественные методы в менеджменте. РГЭУ, 2008 | |
| Дополнительная литература | ||
| 1. | Кузнецов О.П.Адельсон-Вельский Г.М. Дискретная математика для инженеров. М:Энергоатомиздат.1988 | |
| 2. | О.О.Замков, А.В.Толстопятенко, Ю.Н.Черемных Математические методы в экономике. М.: “ДИС”,1997 | |
| 3. | Саати Т.Л. Математические модели конфликтных ситуаций. M., 1977. | |
| 4. | Коханенко И.К. Технология “fuzzy logic” при оценке качества услуг. // Методы менеджмента качества №5, 2004 |
3.2.Материально-технические
| № ауд. | Основное оборудование, стенды, макеты, компьютерная техника, наглядные пособия и другие дидактические материалы, обеспечивающие проведение лабораторных и практических занятий, научно-исследовательской работы студентов с указанием наличия | Основное назначение (опытное, обучающее, контролирующее) и краткая характеристика использования при изучении явлений и процессов, выполнении расчетов. |
| Компьютерная техника. | PowerPoint, AdobeAcrobat |
4. Текущий, промежуточный контроль знаний студентов
| № | Тесты, темы курсовых работ/проектов, вопросы для текущего контроля, для подготовки к зачету, экзамену |
| 1. | 4.1. Задания для текущего контроля |
| 2. | Решить игровую задачу, если платежная матрица имеет вид:
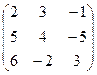 . .
|
| 3. | Решить игру с платежной матрицей A графическим методом |
| 4. | Найти кратчайший путь в заданном ориентированном графе G. |
| Рассчитать максимальный поток в заданном графе. | |
| 4.2.Темы контрольных работ | |
| Модуль 1. Игры, разрешимые в смешанных стратегиях. | |
| Модуль 2. Оптимизационные задачи на графах. | |
4.3.Вопросы к экзамену за третий семестр
1. Основные понятия и базовые принципы теории игр
2. Классификация игр и методы представления.
3. Платежная матрица. Нижняя и верхняя цена игры
4. Оптимальные стратегии в условиях неопределенности. Устойчивость игровых моделей
5. Выбор оптимального решения игр в смешанных стратегиях
6. Приведение матричной игры к задаче линейного программирования
7. Схема решения произвольной конечной игры размера m × n
8. Проблема оптимального решения в теории игр. Типы равновесий
9. Проблемы менеджмента при различных ситуациях равновесия и способы их разрешения
10. Модель олигополистического рынка
11. Моделирование дуополии
12. Дилемма заключенного как типичная игра олигополистического рынка
13. Принцип Парето-оптимальности и его приложения
14. Позиционные игры
15. Проблемы управления в процессе конфликтного взаимодействия
16. Коллективные решения
17. Отношения. Матричный способ их представления
18. Композиция бинарных отношений
19. Свойства отношений и операций над ними
20. Законы композиции. Алгебраическая система
21. Классы алгебраических систем
22. Графы, основные понятия
23. Способы описания графов
24. Матрицы графов
25. Изоморфизм графов. Маршрут, цепь, цикл, путь, контур
26. Знаковые графы.Критерии сбалансированности графа
27. Сети Петрикак инструмент исследования систем. Основные свойства сетей Петри
28. Простые сети Петри
29. Цветные сети Петри.Точки доступа
30. Анализ сетей Петри.
31. Типовая менеджерская задача с сетями Петри
32. Приложения теории графов к изучению организации и управления
33. Задача измерения статуса подчиненности служебного лица
34. Построение меры значимости субъекта в структуре коммуникативной связи организации
35. Задача о клике
36. Знаковые графы и когнитивные технологии в менеджменте
37. Когнитивные карты ситуации
38. Вопросы обеспечения целенаправленного поведения в сложной ситуации
Образец экзаменационного билета
1. Понятие графа. Классификация графов.
2. Критерий разрешимости игры в чистых стратегиях.
3. Решить игровую задачу, если платежная матрица имеет вид:
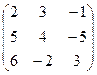 . .
|
5. Дополнения и изменения в рабочей программе на учебный год _____/______
| Следующие записи относятся к п.п. |
| Автор |
| Зав. кафедрой |
Принято УМУ__________________________________ Дата:_____________________
6. По дисциплине «Количественные методы в менеджменте» для студентов заочного отделения специальности «Управление персоналом» предлагается выполнение контрольную работу работы. Прежде чем выполнить эту работу, студент должен разобраться в основных понятиях и методах соответствующей темы, прочитав соответствующую лекцию и дополнив, если необходимо, изучением соответствующего раздела по учебнику. Затем необходимо разобрать решение типичных примеров и задач по соответствующей теме, решить примеры домашнего задания по данной теме. Для закрепления материала необходимо продумать ответы на контрольные вопросы к зачету или экзамену по данной теме.
Глоссарий
Алгебраической системой <A;F;R> называется объект, состоящий из трёх множеств: непустого множества A, множества алгебраических операций F, определённых на A, и множества отношений R, определённых на A.
Бинарными отношениями (двухместными) называются отношения между двумя множествами Х и Y, устанавливающие соответствие элементов множества Х элементам множества Y.
Графом называется двуосновная модель <V, E; i >, где i – бинарное отношение множеств V и E, такое, что каждый элемент e E находится в отношении i либо ровно с одним, либо ровно с двумя элементами множества V.
Игра - математическая модель игровой ситуации принятия решений, характеризуемая следующими особенностями:
1. наличие не менее двух участников, имеющих разные интересы - конфликтность;
2. наличие у каждого из участников нескольких вариантов поведения - стратегий (неопределенность);
3. результаты, получаемые игроками (платежи), зависят от стратегий, выбранных всеми участниками - взаимозависимость поведения;
4. наличие правил игры, определяющих возможные стратегии игроков, последовательность их действий, их информированность, получаемые результаты и т.д.
Матрица инцидентностипредставляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа.
Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа), однозначно представляющая его структуру.
Оптимальное решение (или решение) игры (на основании принципа минимакса) - это пара оптимальных стратегий S*A, S*B в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей
Сеть первого рода - это цветная сеть Петри, описанная на языке предписаний.
Стратегия игрока - совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации.
Частично-упорядоченным множеством называется модель <A; >, бинарное отношение которой удовлетворяет системе аксиом:
· для любого элемента a A выполняется (a, a) (или a a);
· для любых элементов a, b A, из a b, b a следует a = b;
· для любых элементов a, b, c A, таких что a b, b c выполняется a b.
Курс лекций
Основные понятия и базовые принципы теории игр
Игра - математическая модель игровой ситуации принятия решений, характеризуемая следующими особенностями:
1. наличие не менее двух участников, имеющих разные интересы - конфликтность;
2. наличие у каждого из участников нескольких вариантов поведения - стратегий (неопределенность);
3. результаты, получаемые игроками (платежи), зависят от стратегий, выбранных всеми участниками - взаимозависимость поведения;
4. наличие правил игры, определяющих возможные стратегии игроков, последовательность их действий, их информированность, получаемые результаты и т.д.
Игроки - стороны, участвующие в конфликтной ситуации (i). Обозначим множество всех игроков как I={1,2,…, N}.
Выигрыш (проигрыш) – исход конфликта.
Правила, вводимые для каждой формализованной игры, - система условий, определяющая:
1. варианты действий игроков;
2. объем информации каждого игрока о поведении партнеров;
3. выигрыш, к которому приводит каждая совокупность действий.
Как правило, выигрыш (или проигрыш) может быть задан количественно; например, можно оценить проигрыш нулем, выигрыш — единицей, а ничью — 1/2.
Ход игрока - выбор и осуществление одного из предусмотренных правилами действий. Ход может быть:
· личным - сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре);
· случайным - случайно выбранное действие (например, выбор карты из перетасованной колоды). В дальнейшем мы будем рассматривать только личные ходы игроков.
Стратегии (si) - последовательные или одновременные действия (решения) игроков. Для каждого игрока задается множество стратегий Si.
Стратегия игрока - совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации. Обычно в процессе игры при каждом личном ходе игрок делает выбор в зависимости от конкретной ситуации. Однако в принципе, возможно, что все решения приняты игроком заранее (в ответ на любую сложившуюся ситуацию). Это означает, что игрок выбрал определенную стратегию, которая может быть задана в виде списка правил или программы. (Так можно осуществить игру с помощью ЭВМ).
Профиль стратегий sN={s1,s2,..,sN} - набор стратегий, выбранных каждым из игроков. Профиль стратегий определяют платежи игроков.
Платежная функция ui - некая результатная величина, существующая для каждого игрока. Каждый игрок выбирает свою стратегию si из Si. После того, как это сделают все, определяется платеж игрока ui (sN).
Множество чистых стратегий - множество Si.
Игра решается в чистых стратегиях, если игроки выбирают по одной стратегии из своих множеств стратегий, и выбирали бы эти же стратегии всякий раз при повторении игры.
Смешанная стратегия игрока - это комбинации чистых стратегий, выбираемых в определенном сочетании или с определенной вероятностью. Для неко
|
|
|


