Выбор оптимального решения игр в смешанных стратегиях

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. Так, в примере1 α=-1 ≠ β=1, седловая точка отсутствует. В этом случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий A₁,A₂,...,A_m с вероятностями p₁,p₂,...,p_i,...,p_m. Причем сумма вероятностей равна 1:

Смешанные стратегии игрока А записываются в виде матрицы:

или в виде строки SA = (p1,p2,...,pi,...,pm)

Аналогично смешанные стратегии игрока В обозначаются:

или в виде строки SB = (q1,q2,...,qj,...,qn),

где сумма вероятностей появления стратегий также равна 1: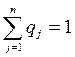

Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой 1 соответствует чистой стратегии.

Оптимальное решение (или решение) игры (на основании принципа минимакса) - это пара оптимальных стратегий S*_A, S*_B в общем случае смешанных, обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей.

Выигрыш, соответствующий оптимальному решению, называется ценой игры v. Цена игры удовлетворяет неравенству: α ≤ v ≤ β, где α и β — нижняя и верхняя цены игры.

Справедлива следующая основная теорема теории игр - теорема Неймана:

 

каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

 

Пусть S*_A = (p*₁,p*₂,...,p*_i,...,p*_m) и S*_B = (q*₁,q*₂,...,q*_j,...,q*_n) - пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Справедлива теорема об активных стратегиях:

если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Эта теорема имеет большое практическое значение, так как она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.

Рассмотрим игру размера 2×2, которая является простейшим случаем конечной игры.

Если такая игра имеет седловую точку, то оптимальное решение - это пара чистых стратегий, соответствующих этой точке.

Для игры, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий S*_A = (p*₁, p*₂) и S*_B = (q*₁, q*₂).

Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок А придерживается своей оптимальной стратегии S*_A, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией ни пользовался игрок В.

Для игры 2×2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока А (проигрыш игрока В) - случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока А (оптимальная стратегия) будет равен v и для 1-й – B₁, и для 2-й - B₂ стратегии противника.

Пусть игра задана платежной матрицей /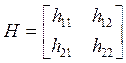

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию , а игрок В - чистую стратегию B₁ (это соответствует 1-му столбцу платежной матрицы H), равен цене игры v:

h₁₁ p*₁+ h₂₁ p*₂= v.

Тот же средний выигрыш получает игрок А, если игрок B применяет стратегию B₂, т.е.

h₁₂ p*₁+ h₂₂ p*₂= v.

Учитывая, что p*₁+p*₂=1, получаем систему уравнений для определения оптимальной стратегии S'_A и цены игры v:

Решая эту систему, получим оптимальную стратегию игрока А:

и цену игры: .

Применяя теорему об активных стратегиях при отыскании S*_В- оптимальной стратегии игрока В, получаем, что при любой чистой стратегии игрока А (А₁ или А₂) средний проигрыш игрока В равен цене игры v, т.е.

Тогда оптимальная стратегия игрока В определяется формулами:

 

Пример 4.

Найти оптимальные стратегии игры «Поиск» размера 2×2 (см. пример1).

Решение.

Игра "Поиск" задана платежной матрицей:

.

Нижняя и верхняя цены игры соответственно равны α=-1 и β=1 (см. пример 2), т.е. игра не имеет седловой точки. Поэтому оптимальные стратегии игры будем искать в смешанных стратегиях.

Для игрока А средний выигрыш равен цене игры v (при B₁ и B₂); для игрока В средний проигрыш равен цене игры v (при A₁ и А ₂).

Системы уравнений в данном случае имеют вид:

 

 

Решая эти системы, получим р^*₁=р^*₂=q^*₁=q^*₂= , v=0.

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью , при этом средний выигрыш равен 0.

1.9 Геометрическая интерпретация игры 2×2

Решение игры 2×2 допускает наглядную геометрическую интерпретацию.

Пусть игра задана платежной матрицей Н=[hij], где i,j = 1,2.

По оси абсцисс (рисунок 4) отложим единичный отрезок A₁A_2. Точка A₁(х=0) изображает стратегию A₁, а все промежуточные точки этого отрезка - смешанные стратегии S_A первого игрока, причем расстояние от S_A до правого конца отрезка - это вероятность p₁ стратегии A₁, расстояние до левого конца - вероятность p₂ стратегии A₂.

На перпендикулярных осях I—I и II—II откладываем выигрыши при стратегиях A₁ и A₂ соответственно. Если 2-й игрок примет стратегию B₁, то она дает выигрыши h₁₁ и h₂₁ на осях I—I и II—II, соответствующие стратегиям A₁ и A₂. Обозначим эти точки на осях I—I и II—II буквой B₁. Средний выигрыш v ₁, соответствующий смешанной стратегии S_A, определяется по формуле математического ожидания v ₁ = h₁₁ p₁ + h₂₁ p₂ и равен ординате точки M₁, которая лежит на отрезке B₁ B₁ и имеет абсциссу S_A (рисунок 4).

 

Рисунок 4	Рисунок 5

 

Аналогично строим отрезок B₂B₂, соответствующий применению вторым игроком стратегии B₂ (рисунок 5).

При этом средний выигрыш ν₂ =h₁₂ p₁ + h₂₂ p₂ - ордината точки M₂.

В соответствии с принципом минимакса оптимальная стратегия S*_A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рисунок 6), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке B₁N - против стратегии B₁ , на участке NB₂ - против стратегии B₂).

Оптимальную стратегию S*_A = (p*₁ p*₂) определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры v. На рисунке 6 обозначены также верхняя и нижняя цены игры α и β.

Пусть Н=

Определим оптимальную стратегию игрока А геометрическим методом

Откладываем по оси абсцисс (рисунок 7) единичный отрезок A₁A₂.

На вертикальной оси I-I откладываем отрезки: h₁₁, соответствующий стратегии B₁, и h₁₂, соответствующий стратегии B₂.

На вертикальной оси II—II отрезок h₂₁ соответствует стратегии B₁ , отрезок h₂₂ соответствует стратегии B₂ (рисунок 7).

Нижняя цена игры α=h₂₂ – наибольшему из наименьших.

Верхняя цена игры β =h₁₂ ( наименьшему из наибольших ), в нашем случае на графике показано, что седловая точка отсутствует. Из рисунка 7 видно, что

· абсцисса точки N определяет оптимальную стратегию S*_A,

· ордината — цену игры v.

Точка N является точкой пересечения прямых B₁B₁ и B₂B₂.

Рисунок 6	Рисунок 7

Уравнение прямой B₁B₁, проходящей через точки (0; h₁₁) и (1; h₂₁):

или y = х(h₂₁-h₁₁)+h₁₁.

Уравнение прямой B₂B₂, проходящей через точки (0; h₁₂) и (1; h₂₂):

или y = х(h₂₂-h₁₂)+h₁₂.

Точка пересечения прямых является решением системы:

Решив систему, можно найти x и y, т.е. координаты точки N(х; у)

Тогда p*₂= х, p*₁= 1 - х;

оптимальная стратегия S*_A = (1-х; х),

цена игры v = у

Определение оптимальной стратегии игрока В.

Оптимальную стратегию игрока В геометрически можно определить, если поменять местами игроков А и В и вместо максимума нижней границы A₂MA₁ в соответствии с принципом минимакса рассмотреть минимум верхней границы.

Абсцисса точки М определяет q*₂ в оптимальной стратегии игрока В, ордината этой точки — цена игры.

Прямая A₁A₁, проходящая через точки (0; h₁₁) и (1; h₁₂), удовлетворяет уравнению y = х(h₁₂-h₁₁)+h₁₁.

Прямая A₂A₂, проходящая через точки (0; h₂₁) и (1; h₂₂), удовлетворяет уравнению у = х(h₂₂-h₂₁)+h₂₁.

Координаты их точки пересечения М - это решение системы уравнений:

.

 

Откуда найдем x и y М(х; у)

q*₂= х, q*₁= 1 - х

v = y S*_B = (1-х; х)

Оптимальное решение игры найдено.

Из решения задачи следует, что геометрически можно определять оптимальную стратегию как игрока А, так и игрока В, в обоих случаях используется принцип минимакса, но во втором случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.

Если платежная матрица содержит отрицательные числа, то для графического решения задачи лучше перейти к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число. Решение игры при этом не изменится, а цена игры увеличится на это число.

В примере 4 платежная матрица не имела седловой точки (α ≠β).

При наличии седловой точки графическое решение дают варианты, изображенные на рисунке 8 и 9. На рисунке 8 наибольшей ординатой на ломаной B₁NB₂ обладает точка B₂, поэтому оптимальной является чистая стратегия A₂ для игрока А (B₂ - для игрока В), т.е. оптимальное решение:

S*_A = (0;1), S*_B = (0;1).

Игра имеет седловую точку h₂₂ = v.

 

Рисунок 8	Рисунок 9

 

Чистая стратегия B₂ (рисунок 9) не выгодна для игрока В, поскольку при любой стратегии игрока А она дает последнему больший выигрыш, чем чистая стратегия B₁.

На основании принципа минимакса выделим прямую B₁B₁ и на ней точку B₁ с наибольшей ординатой на оси I-I. Чистая стратегия A₂ является оптимальной для игрока А, а чистая стратегия B₁ - для игрока В.

Оптимальное решение: S*_A = (0;1), S*_B = (1;0),

цена игры v = h₂₁ = α = β, т.е. имеется седловая точка.

Замечание:

графический метод можно применять при решении игры 2 × n и m × 2.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: