 |
Нечетные МОЭ для случая экваториально намагниченной пластинки
|
|
|
|
Рассмотрим экваториально намагниченную ферромагнитную пластинку, помещенную между двумя диэлектрическими средами с показателями преломления n1 и n3 (рис. 2).Если на такую пластинку из среди 1 падает плоская монохроматическая волна (1.3), то в силу линейности граничных условий (1.2), отраженная, прошедшая и преломленные волна будут также плоскими и монохроматическими. Опуская общий для всех волн временной множитель exp(iwt), зададим напряженности электрического поля падающей, отраженной и прошедшей волн ввиде:
 1 (
1 (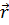 ) =
) =  ∙exp (-i
∙exp (-i 
 1
1 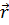 ),
),
 (
(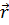 ) =
) =  exp (-i
exp (-i 
 ), (1.12)
), (1.12)
 3 (
3 (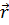 ) =
) =  exp [-i
exp [-i 
 3(
3(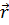 -
-  d2)],
d2)],
где q = (1,0,0) - орт нормали к пластинке,  1,
1,  ,
,  3 - вектора рефракции волн, d2 - толщина пластинки. Под действием падающей световой волны в намагниченной пластинке возбуждается система преломленных волн
3 - вектора рефракции волн, d2 - толщина пластинки. Под действием падающей световой волны в намагниченной пластинке возбуждается система преломленных волн
 v (
v (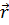 ) = Ev
) = Ev  v exp (-i
v exp (-i 
 2v
2v 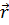 ), (1.13)
), (1.13)
где  v - единичный вектор поляризации напряженности электрического поля и
v - единичный вектор поляризации напряженности электрического поля и  2v - соответствующий вектор рефракции V - той волны, известные из решения волнового уравнения (1.7). Всего возбуждается 4 таких волны: две прямые, распространяющиеся от верхней границы пластинки, и две, отраженные от её нижней границы.
2v - соответствующий вектор рефракции V - той волны, известные из решения волнового уравнения (1.7). Всего возбуждается 4 таких волны: две прямые, распространяющиеся от верхней границы пластинки, и две, отраженные от её нижней границы.
Выберем систему координат как показано на рис. 2, направив ось x по нормали к границе раздела, ось у по линии пересечения плоскости раздела и плоскости падения света и ось z перпендикулярно плоскости падения света. При экваториальном намагничивании орт намагниченности  направлен вдоль оси z и задается в виде
направлен вдоль оси z и задается в виде

Рис.2. Геометрия отраженной и преломленных волн в экваториально намагниченной пластинке
 = (0, 0,
= (0, 0,  ),
),  = ±1. (1.14)
= ±1. (1.14)
Как известно [35], вектор рефракции всех волн, фигурирующих в граничной задаче падающей, отраженной, преломленной и прошедшей, лежат в плоскости падения света и в выбранной нами системе координат определяются в виде
|
|
|
nj = (gj, -n1  , 0), (1.15)
, 0), (1.15)
где j - индекс волны, j - угол падения света на внешнюю границу. Параметр gj, представляющий проекцию вектор рефракции j - той волны на направление нормали, связан с показателем преломления nj этой волны выражением
gj =  , (1.16)
, (1.16)
Имея в виду рассмотрение в дальнейшем нечетных МОЭ, ограничимся в формулах (1.10), (1.11) учетом лишь линейных по намагниченности членов. Кроме того, положим диагональные магнитные проницаемости всех сред равными единице. В частности, для ферромагнитной среды μ0 = μ = 1. При этом, однако, недиагональная компонента тензора магнитном проницаемости ферромагнетика остается отличной от нуля: μxy = -iM ≠ 0. В указанном приближении показатели преломления волн, распространяющихся в экваториально намагниченной среде (1.10), равны между собой
n21 = n22 ≡ n2 = 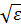 , (1.17)
, (1.17)
где n2 - оптический показатель преломления ненамагниченного ферромагнетика. Вектора рефракции (1.15) преломленных в пластинке волн (1.13) равны:
 21 =
21 =  22 =
22 =  2 = (g2 , -n1
2 = (g2 , -n1  , 0),
, 0),
(1.18)
 21 =
21 =  22 =
22 =  2 = (-g2 , -n1
2 = (-g2 , -n1  , 0),
, 0),
где  2 - вектор рефракции отраженной (отмечаемой штрихом) волны и, согласно (1.16)
2 - вектор рефракции отраженной (отмечаемой штрихом) волны и, согласно (1.16)
g2 =  . Вектора поляризации (1.11) волн в пластинке в линейном по намагниченности приближении записываются в виде
. Вектора поляризации (1.11) волн в пластинке в линейном по намагниченности приближении записываются в виде
 1 =
1 =  1 = (0, 0, -
1 = (0, 0, -  ),
),
 2 =
2 =  2 = (0, 0, n2
2 = (0, 0, n2  ),
),
(1.19)
 1 = (n1
1 = (n1  + ig2M, g2 – in1M
+ ig2M, g2 – in1M  , 0),
, 0),
 1 = (n1
1 = (n1  – ig2M, -g2 – in1M
– ig2M, -g2 – in1M  , 0),
, 0),
 2 =
2 =  (n1
(n1  + ig2Q, g2 – in1Q
+ ig2Q, g2 – in1Q  , 0),
, 0),
 2 =
2 =  (n1
(n1  – ig2Q, -g2 – in1Q
– ig2Q, -g2 – in1Q  , 0),
, 0),
где γ - угол (0 или  ) между ортом намагниченности
) между ортом намагниченности  и осью z;
и осью z;  = ±1.
= ±1.
Используя поперечность световых волн в средах 1 и 3, можно разложить амплитуды напряженностей электрического поля падающей, отраженной и прошедшей волн (1.12) на s - и р - составляющие
 = As
= As 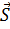 + Ap
+ Ap  ,
,
(1.20)
 = Rs
= Rs 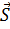 + Rp
+ Rp  ,
,
 = Ts
= Ts 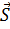 + Tp
+ Tp  3,
3,
где вектор 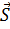 = (0,0,1) перпендикулярен плоскости падения света, и единичные вектора
= (0,0,1) перпендикулярен плоскости падения света, и единичные вектора
 j =
j =  (-n1
(-n1  , -gj, 0), (1.21)
, -gj, 0), (1.21)
перпендикулярно вектору 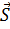 и световому лучу, лежат в плоскости падения. Компоненты отраженной Rs, Rp и прошедшей Ts, Tp волн связаны с компонентами As, Ap падающей волны с помощью матриц отражения (r) и пропускания (t)
и световому лучу, лежат в плоскости падения. Компоненты отраженной Rs, Rp и прошедшей Ts, Tp волн связаны с компонентами As, Ap падающей волны с помощью матриц отражения (r) и пропускания (t)
|
|
|
 =
= 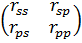 ∙
∙  ;
;  =
=  ∙
∙  . (1.22)
. (1.22)
Элементы матриц отражения и пропускания, а также скалярные амплитуды Е v преломленных волн (1.13) находятся из решения системы граничных уравнений (1.2) для пластинки с использованием значений показателей преломления (1.17) и векторов поляризации (1.19) волн в пластинке.
Введем предварительно систему френелевских коэффициентов отражения (r) и пропускания (t) для многослойных систем. Коэффициенты отражения и пропускания на границе раздела i – той и j - той сред при S - и P - поляризации падающей волны даются известными выражениями
 =
=  ;
;  =
= 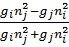 ,
,
(1.23)
 =
=  ;
;  =
=  ,
,
где параметры  ,
,  определены выражениями (1.16). Заметим, что в (1.16) ni - показатель преломления внешней среды, из которой свет падает на систему под углом j. Для последовательности сред i, j, k,…. (в частности, например, 1, 2, 3, 4,…), разделенных плоскими границами, имеют место следующие рекуррентные формулы для коэффициентов отражения и пропускания в случае однослойной, двухслойной и т.д. систем [51]:
определены выражениями (1.16). Заметим, что в (1.16) ni - показатель преломления внешней среды, из которой свет падает на систему под углом j. Для последовательности сред i, j, k,…. (в частности, например, 1, 2, 3, 4,…), разделенных плоскими границами, имеют место следующие рекуррентные формулы для коэффициентов отражения и пропускания в случае однослойной, двухслойной и т.д. систем [51]:
 =
= 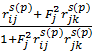 ,
, 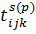 =
=  ,
,
(1.24)
 =
=  ,
,  =
=  ,
,
где величины
 = exp (-2πiλ-1
= exp (-2πiλ-1  ). (1.25)
). (1.25)
представляют собой фазовые множители, определяющие набег фазы волн с длиной λ и ее затухание в j - том слое с толщиной di.
С учетом записанных выражений результаты расчета матриц отражения и пропускания (1.22) для экваториально намагниченной пластинки могут быть представлены следующим образом. Недиагональные элементы матриц равны нулю:
 =
=  =
=  =
=  = 0. (1.26)
= 0. (1.26)
Диагональные элементы в линейном по намагниченности приближении записываются в виде
 =
=  (1 + iρs),
(1 + iρs),  =
=  (1 + iρp),
(1 + iρp),
(1.27)
 =
=  (1 + iτs),
(1 + iτs), 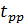 =
=  (1 + iτp),
(1 + iτp),
где  =
=  и
и  =
=  - коэффициенты отражения и пропускания для ферромагнитной пластинки в отсутствие намагниченности, определенные формулами (1.24). Нечетные по намагниченности поправки к элементам матрицы пропускания даются выражениями
- коэффициенты отражения и пропускания для ферромагнитной пластинки в отсутствие намагниченности, определенные формулами (1.24). Нечетные по намагниченности поправки к элементам матрицы пропускания даются выражениями
 =
=  ,
,
(1.28)
 =
=  ,
,
Поправки к элементам матриц отражения равны
 =
=  ,
,
(1.29)
 =
=  .
.
В формулах (1.28) и (1.29): n1 и n2 - показатели преломления внешней среды и пластинки,  и т.д.-коэффициенты отражения (1.23), F2 (1.25) - фазовый множитель для пластинки, Q и М - первый и второй магнитооптические параметры, j - угол падения света из внешней среды на пластинку,
и т.д.-коэффициенты отражения (1.23), F2 (1.25) - фазовый множитель для пластинки, Q и М - первый и второй магнитооптические параметры, j - угол падения света из внешней среды на пластинку,  = ± 1.
= ± 1.
|
|
|
Перейдем к рассмотрению самих экваториальных эффектов. МОЭ, возникающие при взаимодействии света с намагниченной пластинкой, представляют собой связанные с намагниченностью изменения интенсивности и состояния поляризации отраженной и прошедшей волн. Интенсивности падающей, отраженной и прошедшей волн согласно (1.20) равны
J =  ,
,  =
= 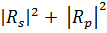 ,
,  =
=  . (1.30)
. (1.30)
Обозначим через  и
и  интенсивности прошедшей волны, относящиеся соответственно к намагниченному к размагниченному состояниям образца. Тогда при учете (1.22), (1.26), (1.27), нечетный эффект относительного изменения интенсивности света при его прохождении через экваториально намагниченную пластинку дается выражением
интенсивности прошедшей волны, относящиеся соответственно к намагниченному к размагниченному состояниям образца. Тогда при учете (1.22), (1.26), (1.27), нечетный эффект относительного изменения интенсивности света при его прохождении через экваториально намагниченную пластинку дается выражением
 =
= 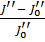 =
=  . (1.31)
. (1.31)
Аналогично, величина относительного изменения интенсивности света, отраженного от экваториально намагниченной пластинки, находится в виде
 =
=  =
=  . (1.32)
. (1.32)
Состояние поляризации плоской волны удобно описывать с помощью комплексного в общем случае угла поляризации, определяемого для падающей, отраженной и прошедшей волн выражениями
tg  =
=  , tg
, tg  =
=  , tg
, tg  =
=  . (1.33)
. (1.33)
При этом угол  наклона большой оси эллипса поляризации волны к направлению вектора
наклона большой оси эллипса поляризации волны к направлению вектора 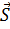 = (0, 0, 1) и эллиптичность
= (0, 0, 1) и эллиптичность  связаны с углом
связаны с углом  соотношениями
соотношениями
 = Re
= Re  ,
,  =
=  . (1.34)
. (1.34)
Обозначив через  ,
,  ,
,  ,
,  углы поляризации отраженной и прошедшей волны соответственно для намагниченной и размагниченной пластинки. Линейные по намагниченности изменения углов поляризации при отражении и пропускании света в случае акваториально намагниченной пластинки выражаются следующими формулами:
углы поляризации отраженной и прошедшей волны соответственно для намагниченной и размагниченной пластинки. Линейные по намагниченности изменения углов поляризации при отражении и пропускании света в случае акваториально намагниченной пластинки выражаются следующими формулами:
Δ  =
=  ,
,
(1.35)
Δ  =
=  ,
,
Величины  = ReΔ
= ReΔ  и
и  = ReΔ
= ReΔ  представляют собой измеряемые углы поворота плоскости поляризации отраженной и прошедшей волны. Если ввести с помощью формул (1.33)
представляют собой измеряемые углы поворота плоскости поляризации отраженной и прошедшей волны. Если ввести с помощью формул (1.33)
 =
=  ,
,  =
=  , (1.36)
, (1.36)
углы поляризации  и
и  для размагниченного образца, то выражения (1.35) могут быть представлены в виде
для размагниченного образца, то выражения (1.35) могут быть представлены в виде
Δ  =
=  ,
,
(1.37)
Δ  =
= 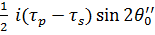 ,
,
Наиболее интересный случаи имеет место при S - (Ар = 0) или Р - (As = 0) поляризации падающей волны. При этом эффекты изменения интенсивности прошедшего (1.31) и отраженного (1.32) света выражаются формулами
|
|
|
 ,
,  ,
,
(1.38)
 ,
,  ,
,
а эффекты изменения состояния поляризации (1.37) равны нулю:
 =
=  =
= 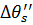 =
=  = 0. (1.39)
= 0. (1.39)
Как видно из выражений (1.28) и (1.29), величины  пропорциональны недиагональной компоненте
пропорциональны недиагональной компоненте  тензора магнитной проницаемости (1.9), в то время как поправки
тензора магнитной проницаемости (1.9), в то время как поправки  и
и  связаны только с недиагональной компонентой
связаны только с недиагональной компонентой  тензора диэлектрической проницаемости. Поэтому эффекты изменения интенсивности (1.38) при S - и P - поляризации падающей волны являются соответственно чисто гиромагнитными и чисто гироэлектрическими. Эффекты изменения интенсивности прошедшего света
тензора диэлектрической проницаемости. Поэтому эффекты изменения интенсивности (1.38) при S - и P - поляризации падающей волны являются соответственно чисто гиромагнитными и чисто гироэлектрическими. Эффекты изменения интенсивности прошедшего света  и
и  , ранее не наблюдавшиеся, представляют собой новый тип МОЭ, в которых происходит разделение гироэлектрических и гиромагнитных свойств ферромагнетиков.
, ранее не наблюдавшиеся, представляют собой новый тип МОЭ, в которых происходит разделение гироэлектрических и гиромагнитных свойств ферромагнетиков.
Обратимся к рассмотрению некоторых особенностей экваториальных эффектов в прошедшем свете. Прежде всего следует отметить, что нечетные экваториальные эффекты изменения интенсивности и состояния поляризаций прошедшей волны, так же как и аналогичные эффекты при отражении света, существуют лишь при наклонном падении света и имеют ярко выраженный граничный характер. Их происхождение, в отличии, например, от эффекта Фарадея, связано не с двойным лучепреломлением, которое, как видно из (1.17), в данной геометрии отсутствует, а с различным характером отражения и преломления волн на границах намагниченной пластинки. Отсутствие проявления объемных эффектов видно хотя бы из того, что в величины (1.28) и (1.29) не входят члены, пропорциональные толщине магнитного слоя. С определяющим влиянием границ связана главная особенность экваториальных эффектов в прошедшем свете: как следует из выражений (1.28), эти эффекты отличны от нуля лишь при условии, что отличны от нуля разности ( ) коэффициентов отражения света на верхней и нижней границах пластинки. Другими словами, эффекты существуют, если оптические свойства (показатели преломления) граничащих намагниченной пластинкой сред различны. Более детально роль границ при возникновении экваториального эффекта в прошедшем свете можно увидеть, если рассмотреть упрощенный вариант решения граничной задачи в схеме прямого луча.
) коэффициентов отражения света на верхней и нижней границах пластинки. Другими словами, эффекты существуют, если оптические свойства (показатели преломления) граничащих намагниченной пластинкой сред различны. Более детально роль границ при возникновении экваториального эффекта в прошедшем свете можно увидеть, если рассмотреть упрощенный вариант решения граничной задачи в схеме прямого луча.
Если на верхнюю границу экваториально намагниченной пластинки (рис. 2) падает волна, поляризованная в плоскости падения (P - поляризация), то в пластинке возбуждается только одна волна е вектором поляризации  (1.19), эллиптически поляризованная в плоскости падения света. Коэффициент пропускания для этой волны на границе раздела сред 1 и 2 зависит, как нетрудно показать исходя из граничных условий (1.2), от y – составляющей вектора
(1.19), эллиптически поляризованная в плоскости падения света. Коэффициент пропускания для этой волны на границе раздела сред 1 и 2 зависит, как нетрудно показать исходя из граничных условий (1.2), от y – составляющей вектора  и равен
и равен
|
|
|
 =
=  . (1.40)
. (1.40)
На нижней границе пластинки (граница раздела сред 2 и 3) эта волна возбуждает отуженную волну с вектором поляризации 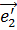 (1.19). Существенно, что пропорциональная Q продольная поправка в y - компоненте отраженной волны имеет другой знак по сравнению с аналогичной поправкой у прямой волны
(1.19). Существенно, что пропорциональная Q продольная поправка в y - компоненте отраженной волны имеет другой знак по сравнению с аналогичной поправкой у прямой волны  . Коэффициент пропускания на границе сред 2 и 3 связан с y - составляющей волны
. Коэффициент пропускания на границе сред 2 и 3 связан с y - составляющей волны 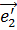 и, аналогично (1.40), находится из выражения
и, аналогично (1.40), находится из выражения
 =
=  . (1.41)
. (1.41)
В приближении прямого луча, т.е. без учета эффектов интерференции, коэффициент пропускания P - поляризованного света через экваториально намагниченную пластинку равен
 12∙
12∙ 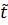 23. (1.42)
23. (1.42)
Из выражения (1.42), при учете (1.40) и (1.41), непосредственно видно, что если показатели преломления граничащих с пластинкой сред равны ( =
=  ), то коэффициент
), то коэффициент 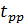 линейных по Q поправок не содержит и, следовательно, нечетные по намагниченности эффекты отсутствуют. Заметим, что формула (1.42) следует из общей формулы (1.27), если в последней пренебречь интерференционными членами (пропорциональными
линейных по Q поправок не содержит и, следовательно, нечетные по намагниченности эффекты отсутствуют. Заметим, что формула (1.42) следует из общей формулы (1.27), если в последней пренебречь интерференционными членами (пропорциональными  ).
).
Аналогичный полученному в (1.40) - (1.42) результат имеет место и в случае, когда падающая волна поляризована перпендикулярно плоскости падения света (S - поляризация). При этом в пластинке возбуждается волна с векторами поляризации  ,
,  (1.19), и существование нечетных эффектов связано с наличием пропорциональной магнитооптическому параметру М продольной составляющей в векторе поляризаций
(1.19), и существование нечетных эффектов связано с наличием пропорциональной магнитооптическому параметру М продольной составляющей в векторе поляризаций  напряженности магнитного поля волны.
напряженности магнитного поля волны.
|
|
|


