Изучение частотной дисперсии эффекта на пленках Fe и Co

 

При изучении электронного энергетического спектра и кинетических характеристик носителей тока ферромагнитных металлов одним из источников информации является частотная зависимость недиагональной компоненты тензора диэлектрической проницаемости . Отождествление ярко выраженных особенностей на экспериментальных кривых дисперсии с определенными оптическими переходами (в рамках расчетного энергетического спектра) позволяет определить, например, спиновую подзону, которой принадлежит данный переход, выделить переходы., матричные элементы которых наиболее сильно подвержены спин-орбитальному взаимодействию. В свою очередь, подобное сопоставление способствует критическому осмыслению корректности того или иного расчета электронного энергетического спектра.

Для определения действительной и мнимой частей величины из измерений магнитооптического эффекта требуется по крайне мере два независимых экспериментальных значения этого эффекта на данной длине волны. В случае экваториального - эффекта в отраженном свете, например, для этого используют его значения при двух углах падения 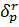(φ) и 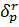(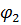). Так же можно поступить и в случае - эффекта в прошедшем свете. С этой целью выражение (3.5) может быть представлено в виде

 

, (3.10)

Где Q = 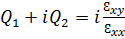, A и B функции угла падения и оптических констант

A = ,

(3.11)

B = ,

 

где

C = . (3.12)

Величины А, В и С найдены в приближении , которое хорошо выполняется в оптическом диапазоне для ферромагнитных металлов.

Решая системы двух уравнений вида (3.10) для двух углов падения и 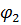, находим значения Q₁ и Q₂. Тогда действительная и мнимая части величины определяются из выражений

,

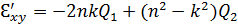(3.13)

,

Измерения частотной дисперсии (Е = ) - эффекта на пленках Fe (толщиной d₂ = 25 нм) и Co (d₂ = 16 нм) были проведены на двухлучевом магнитооптическом спектрометре (параграф 2.2). Результаты этих измерений для углов падения 70° и 80° (Fe) и 70° (Со) представлены на рис. 20. Можно отметить усиление дисперсии эффекта для пленки железа при увеличении угла падения от 70° до 80°. В общем случае зависимость характера дисперсии эффекта от угла падения света следует из формулы (3.5), в которой фактор, определяющий дисперсию, с ростом угла φ меняется от ~ при φ = 0° до ~ при φ = 90°.

Из экспериментальных данных по дисперсий – эффекта при двух углах падения света (70° и 80°) были рассчитаны по (3.13) частотные зависимости действительной и мнимой частей недиагональной компоненты тензора диэлектрической проницаемости пленки железа. Значения действительной и мнимой частей показателя преломления железа 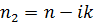взяты из данных для массивного образца [46].

 

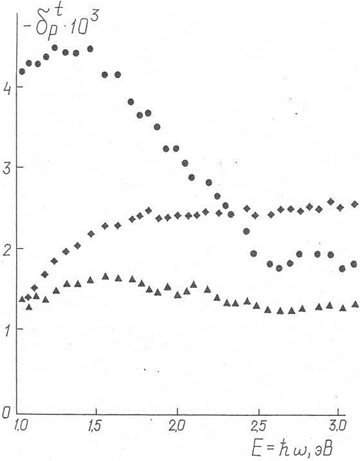
Рис. 20. Частотная дисперсия – эффекта.

● – 80 (Fe), ▲ – 70 (Fe), ♦ - 80 (Co)

 

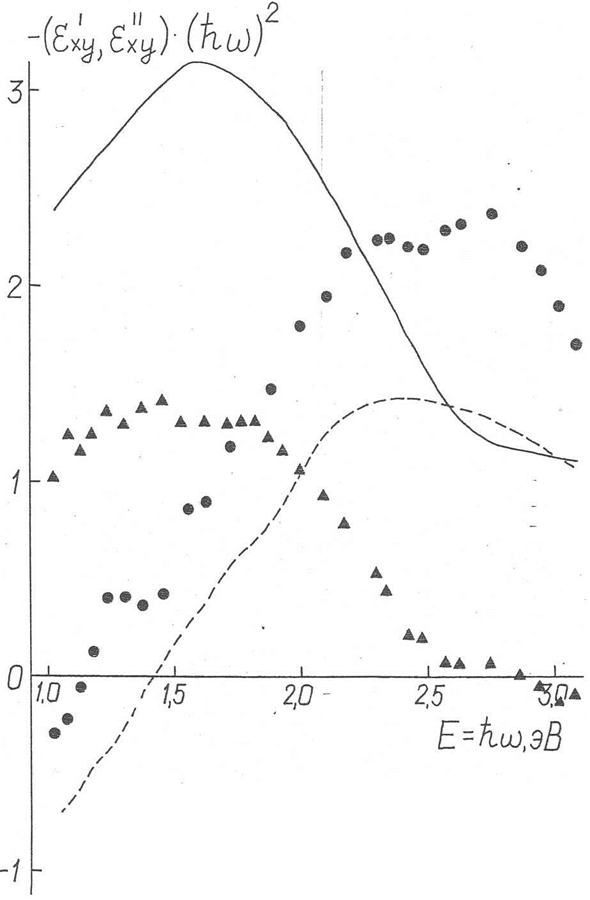
Рис. 21. Дисперсия недиагональных диэлектрической проницаемости железа.

(_____ и ▲) - (, (- - - - - и ●) - (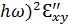, (- - - - - и _______) – данные [10].

(▲ и ●) – данные настоящей работы.

 

 

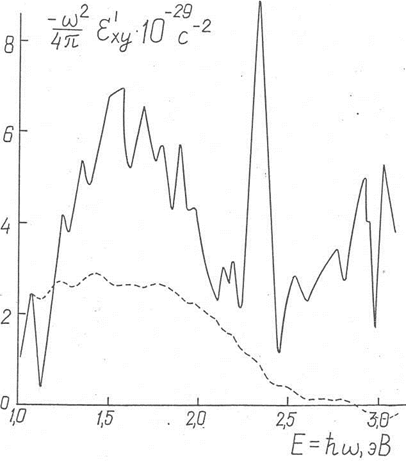
Рис. 22. Дисперсия 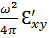для железа.

(______) – расчет [45], (- - - - -) – данные настоящей работы

 

Для стекла (подложка) взято значение показателя преломления 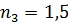и его слабая дисперсия не учитывалась. На рис. 21 приведены рассчитанные спектральные зависимости величин и в интервале энергий 1 - 3,1 эВ. Там же приведены данные по и из [10], где их дисперсия определялась из измерений 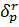- эффекта в отраженном свете для массивных образцов железа. Сравнение результатов, полученных двумя различными методиками, показывает, что они близки по характеру дисперсии, хотя имеются расхождения в абсолютных значениях величин и , особенно заметные для действительной части. Указанное расхождение объясняется, возможно, тем, что при расчете в настоящей работе и в [10] были использованы разные данные по оптическим постоянным железа.

В изученном интервале спектра величина для ферромагнитного железа пропорциональна спин-орбитальной поправке к матричному элементу импульса и определяется механизмом межзонных переходов между состояниями, импульс и волновые функции которых сильно возмущены спин-орбитальным взаимодействием. В [47] дисперсия величины вычислена в рамках самосогласованного расчета зонного спектра ферромагнитного железа. Как следует из рис. 22, где приведены результаты расчета [47] и данные, полученные в настоящей работе, расчет удовлетворительно описывает всплеск межзонного поглощения, приводящий к максимуму () в района 1,5 эВ. Этот всплеск объясняется в [47] наложением переходов, идущих в обширной окрестности центра грани зоны Бриллюэна.

Как показывает проведенное исследование, - эффект может с успехом использоваться наравне с эффектами Фарадея и Керра при изучении магнитооптических свойств ферромагнитных пленочных материалов.

 

3.6. Возможности практического применения - эффекта. Магнитооптический способ определения показателя преломления прозрачных сред

 

В настоящее время МО методы широко используются при определении магнитных характеристик различных материалов [37]. Применение для этой цели нечетных МО эффектов (эффектов Керра и Фарадея) основано на их пропорциональности намагниченности среды.

Исследованный в настоящей работе новый нечетный МО эффект - - эффект также может быть использован наравне (и в сочетании) с известными МО эффектами для изучения магнитного состояния вещества. Помимо величины и её частотной дисперсии (параграфы 3.4 и 3.5), измерение - эффекта дает возможность определить такие практически важные магнитные харктеристищ тонких магнитных пленок, как форма основной кривой намагничивания, форма петли гистерезиса, поле магнитного насыщения H_s и др. Следует отметить возможность исследования состояния намагниченности внутренней (контактирующей с подложкой) границы магнитной пленки путем сравнения кривых намагничивания, полученными от внешней границы с помощью эффекта Керра и от двух границ с помощью – эффекта.

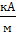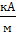На рис. 23 представлена полевая зависимость – эффекта для пленок Fe, Со и Ni, измеренная на длине волны λ =633 нм. По этим кривым можно определить поле магнитного насыщения данных пленок, которые соответственно равны: 7,5 , 3,6 , 1,0 .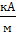

Особенность угловой зависимости - эффекта (обращение его в ноль при угле Брюстера для подложки) открывает неожиданную возможность его применения для определения такой важной оптической характеристики, как показатель преломления прозрачного вещества.

Существуют различные методы определения показателя преломления прозрачных сред: метод призмы, метод предельного угла, эллипсометрический метод. Один из возможных методов основан на определении угла Брюстера [48]. Суть способа заключается в следующем.

Известно, что если на границу прозрачной среды падает световая волна, поляризованная в плоскости падения света, (Р - поляризация) то, согласно формулам Френеля, интенсивность отраженного света связана с интенсивностью J_o падающей волны соотношением:

J = R_p ∙ J_o, (3.14)

 

где

R_p = (3.15)

 

В формуле (3.15) - показатель преломления внешней среды (обычно эта среда - воздух, и тогда = 1в пределах обычной точности измерений), - показатель преломления прозрачной среды, φ - угол падения света. Зависимость отражательной способности R_р от угла падения представлена на рис. 24а. При угле падения Брюстера, который определяется выражением

tg (3.16)

отражательная способность R_р, а вместе с ней и интенсивность отраженного света, обращается в ноль. Зная угол Брюстера можно найти показатель преломления среды.

 

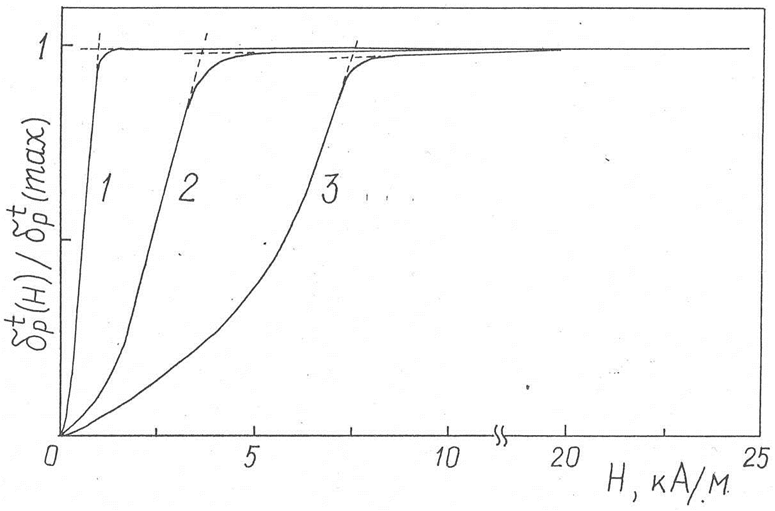
Рис. 23. Вид полевой зависимости эффекта для пленок: 1 - Fe, 2 - Co, 3 - Ni. H_s (1) = 1,0 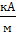, H_s (2) = 3,6 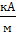, H_s (3) = 7,5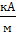

 

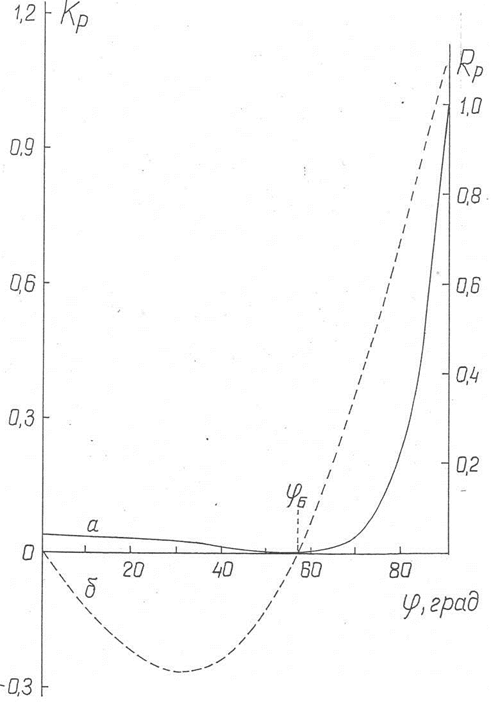
Рис. 24. а – угловая зависимость отражательной способности R_р для диэлектрика с n = 1,5, б – угловая зависимость функции К_р(φ) (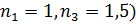

 

Ошибка определения показателя преломления в методе угла Брюстера зависит от ошибки Δφ, с которой измеряется угол падения в минимуме Rр. Ошибка в Δφ, в свою очередь, связана с ошибкой измерения ΔJ - изменения интенсивности отраженного света вблизи угла Брюстера. Окончательная ошибка для в указанном методе выражается формулой

. (3.17)

Невысокая реальная точность этого метода ; ограничения, накладываемые на параллельность светового луча и на толщину образца сильно сужает возможность его применения. Кроме того, повышение точности ограничивается зависимостью ошибки измерения от квадратного корня величины ΔJ/J. Т.е. для увеличения точности измерения на порядок требуется уменьшение ошибки на два порядка. Такая ситуация обусловлена тем, что не только величина R_p(φ), но и её производная при угле Брюстера обращается в ноль (см. рис. 24а).

Предлагаемый новый магнитооптический способ определения показателя преломления прозрачных сред базируется на использовании экваториального – эффекта. Как и в методе угла Брюстера, показатель преломления определяется по формуле (3.16), но сам угол Брюстера находится по обращению в ноль величины - эффекта, что происходит при указанном угле падения. Характерная угловая зависимость величины (φ), как следует из формулы (3.5), определяется, в основном, первым К_p(φ) (3.6) множителем, в то время как второй сомножитель выражения (3.5) в большей степени ответственен за величину эффекта и имеет слабую угловую зависимость.

Совокупность операций магнитооптического способа представляется следующей. На плоскую грань прозрачного образца с показателем преломления (искомым) наносится полупрозрачная ферромагнитная пленка (например, пленка железа толщиной ~ 20 нм). Образец с магнитной пленкой помещается в магнитное поле, которое меняет свою величину от – H_s до Н_s с частотой и направлено перпендикулярно плоскости падения света. Образец освещается монохроматическим светом со стороны магнитной пленки из среды с известным показателем преломления . С помощью фотоприемвого устройства измеряется прошедший через систему пленка - образец световой поток. Изменяется угол падения света φ и фиксируется такое его значение, при котором переменная составляющая на частоте (за счет магнитооптического эффекта) прошедшего светового потока обращается в ноль. Искомый показатель преломления определяется по формуле (3.16).

Как и в методе угла Брюстера, ошибка определения, в магнитооптическом методе связана с ошибкой измерения угла Брюстера соотношением

. (3.18)

Последняя, как и в известном методе, определяется ошибкой, с которой измеряется интенсивность света. Различие, однако, состоит в том, что если в методе угла Брюстера как сама интенсивность J(φ), так и её первая производная 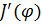при обращается в ноль, то в предлагаемом способе первая производная измеряемой величины J () отлична от нуля (ср. рис. 24а и б). Это открывает возможность повышения точности предлагаемого способа, но сравнению с методом угла Брюстера.

Расчет показывает, что абсолютная ошибка в определении показателя преломления МО методом находится из выражения

. (3.19)

Очевидно, эта ошибка тем меньше, чем больше значение МО эффекта при больших углах падения и чем меньше ошибка ΔJ/J измерения переменной составляющей относительно исходного светового потока. При современном уровне точности измерения интенсивностных эффектов ΔJ/J ~ 10^-7, величине ,

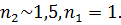
Эта ошибка примерно на порядок меньше, чем для эллипсометрического способа и метода угла Брюстера, которые могут использоваться для образцов в виде пластинок, пленок и слоев.

Вывод: предлагаемый МО способ определения n, являясь технически выполнимым, обладает рядом преимуществ перед известными способами (чувствительность, разнообразие форм образца, отсутствие эталонов, простота оптической настройки) и может найти применение в рефрактометрических методах физики и химии твердого тела.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: