 |
7.2 Обработка результатов исследования со снятием кривой восстановления давления и с учетом притока жидкости к забою после остановки скважины
|
|
|
|
7. 2 Обработка результатов исследования со снятием кривой восстановления давления и с учетом притока жидкости к забою после остановки скважины
В некоторых случаях при исследовании скважины не удается получить прямолинейный участок кривой восстановления давления в координатах  . Чаще всего это объясняется существенным влиянием продолжающегося притока (или оттока) жидкости из пласта в скважину (или наоборот) после ее закрытия на устье. В указанных случаях необходимо обрабатывав данные исследования с учетом притока жидкости в скважину после ее остановки.
. Чаще всего это объясняется существенным влиянием продолжающегося притока (или оттока) жидкости из пласта в скважину (или наоборот) после ее закрытия на устье. В указанных случаях необходимо обрабатывав данные исследования с учетом притока жидкости в скважину после ее остановки.
Для обработки кривых восстановления давления с учетом притока жидкости необходимо одновременно с фиксацией изменения давления на забое регистрировать изменение потока жидкости во времени либо измерять изменение давления на буфере и в затрубном пространстве во времени (для фонтанных и компрессорных скважин), а для насосных скважин определять изменение уровня жидкости в затрубном пространстве.
Имеется несколько методов обработки кривых восстановления давления в скважине с учетом притока жидкости с целью определения параметров пластов и скважин. На основании исследований (сопоставление методов с помощью гипотетической кривой и по результатам исследований скважин высокоточными глубинными манометрами) большинство авторов рекомендуют применять при обработке кривых восстановления давления два метода.
При замедленном притоке жидкости предпочтительнее применять интегральный метод Э. Б. Чекалюка, а при высокой скорости затухания притока следует использовать дифференциальный метод Ю. П. Борисова. Интегральный метод также применяют и в тех случаях, когда кривые восстановления давления имеют разброс точек.
|
|
|
7. 2. 1 Интегральный метод Э. Б. Чекалюка
В данном случае основной формулой является
 (7. 18)
(7. 18)
где D(t) — интеграл Дюамеля;
Q0 — дебит скважины до ее остановки;
V(t) —суммарный приток жидкости в скважину к моменту времени t после ее закрытия на устье.
Если ввести в уравнение (7. 18) координаты 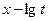 ;
;
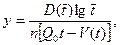 (7. 19)
(7. 19)
где п — масштабный коэффициент, получим прямую линию с угловым коэффициентом
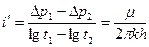 (7. 20)
(7. 20)
и отрезком на оси у
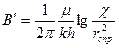 (7. 21)
(7. 21)
Изменение суммарного притока жидкости «в скважину после ее закрытия на устье
 , (7. 22)
, (7. 22)
где Fзат, Fтр — площади сечений столбов жидкости в затрубном пространстве и в подъемных трубах, соответственно;
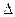 рзаб (t),
рзаб (t), 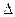 рзат (t),
рзат (t), 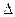 рбуф (t) — приращения давления на забое скважины, в затрубном пространстве и на буфере, начиная от момента ее остановки;
рбуф (t) — приращения давления на забое скважины, в затрубном пространстве и на буфере, начиная от момента ее остановки;
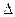
 — плотность нефти в пластовых условиях.
— плотность нефти в пластовых условиях.
Для построения зависимости (7. 18) необходимо вычислить координаты трех-четырех точек. Предварительно кривая восстановления давления строится в специальных координатах  в предположении, что исследование скважины длилось заданное время
в предположении, что исследование скважины длилось заданное время
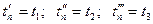
и т. д. Величины G( 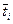 ) определялись с помощью палеток (рис. 7. 3), а интеграл Дюамеля — по предыдущим кривым путем графического интегрирования:
) определялись с помощью палеток (рис. 7. 3), а интеграл Дюамеля — по предыдущим кривым путем графического интегрирования:
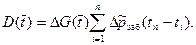 (7. 23)
(7. 23)
Здесь 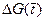 — выбранный шаг по оси абсцисс при определении интеграла.
— выбранный шаг по оси абсцисс при определении интеграла.
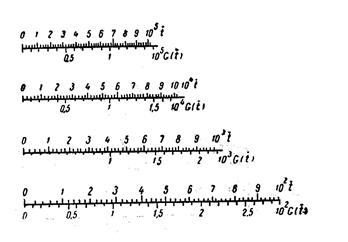
Рис. 7. 3. Палетки для определения вспомогательной функции.
|
|
|
7. 2. 2 Дифференциальный метод Ю. Н. Борисова
Основной расчетной формулой в данном методе является
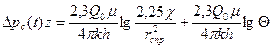 (7. 24)
(7. 24)
где
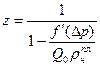 ; (7. 25)
; (7. 25)
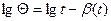 . (7. 26)
. (7. 26)
В формулах (7. 25) и (7. 26):
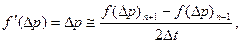 (7. 27)
(7. 27)
где
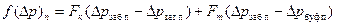 ; (7. 28)
; (7. 28)
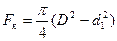 ;
; 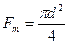 (7. 29)
(7. 29)
где D — внутренний диаметр обсадной колонны скважины;
d1 — внешний диаметр колонны фонтанных труб;
d — внутренний диаметр этой колонны;
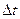 — интервал времени между двумя соседними точками (одинаковый).
— интервал времени между двумя соседними точками (одинаковый).
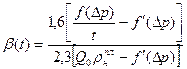 . (7. 30)
. (7. 30)
По прямолинейному участку кривой, построенной в координатах 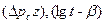 , определяется уклон к оси абсцисс
, определяется уклон к оси абсцисс
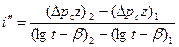 (7. 31)
(7. 31)
и отрезок 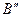 , отсекаемый на оси ординат.
, отсекаемый на оси ординат.
Параметры пласта и скважины определяются по формулам (7. 9)-(7. 11), (7. 15)-(7. 17).
7. 3 Экспресс-метод
Метод предназначен для исследования длительно или временно простаивающих скважин с целью определения их продуктивности (приемистости) и фильтрационных параметров пластов. С теоретической точки зрения этот метод является разновидностью метода восстановления давления. Он разработан для условий, когда давление на забое скважин равно или выше давления насыщения.
Для исследования скважины экспресс-методом применяются два способа возбуждения: подкачка газа и «мгновенный подлив».
При первом способе в скважину, устье которой герметично закрыто, с помощью компрессора или от баллона подкачивается сжатый газ (воздух) с тем, чтобы уровень жидкости был оттеснен на несколько метров или десятков метров.
Основной расчетной формулой при исследовании скважин экспресс-методом с подкачкой в нее газа является
 (7. 32)
(7. 32)
|
|
|
где
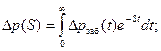 (7. 33)
(7. 33)
 (7. 34)
(7. 34)
Здесь S — постоянное число, рассматриваемое как параметр, который выбирается в зависимости от продолжительности периода исследования в 1/с.
В результате исследования скважины способом подкачки должны быть получены зависимости 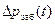 и величины изменения объема жидкости в стволе скважины V(t).
и величины изменения объема жидкости в стволе скважины V(t).
Для построения зависимостей по уравнению (VI. 55) необходимо выбрать несколько значений параметра S. Обычно принимаются 3-4 значения, чтобы минимальная величина S составляла 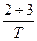 (где Т — общая продолжительность исследований в с), а максимальная S равнялась бы
(где Т — общая продолжительность исследований в с), а максимальная S равнялась бы 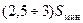 . Промежуточные значения S определяются из приближенных равенств
. Промежуточные значения S определяются из приближенных равенств
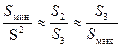 . (7. 35)
. (7. 35)
Интегралы (7. 33) и (7. 34) вычисляются после выделения точек излома линий 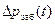 и V(t). Для точек излома выписываются значения координат t с индексами (0, 1, 2, ..., j, j + 1, ..., k) и
и V(t). Для точек излома выписываются значения координат t с индексами (0, 1, 2, ..., j, j + 1, ..., k) и 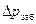 , V с теми же индексами.
, V с теми же индексами.
Интегрирование осуществляется по приближенным формулам
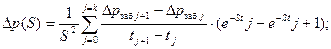 (7. 36)
(7. 36)
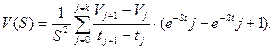 (7. 37)
(7. 37)
По вычисленным значениям  и V(S) находятся отношения
и V(S) находятся отношения 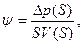 т. е. получаются исходные данные для построения графика
т. е. получаются исходные данные для построения графика 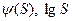 (рис. 7. 4).
(рис. 7. 4).
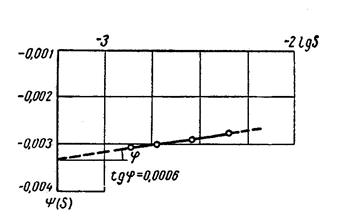
Рис. 7. 4. Зависимость 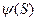 от
от  , построенная по данным исследования скважины с подкачкой газа.
, построенная по данным исследования скважины с подкачкой газа.
Возбуждение непереливающих скважин осуществляется путем быстрого погружения под уровень специальных баллонов, в результате чего уровень «мгновенно» поднимается на величину 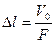 (где V0 — общий объем погружаемых под уровень баллонов; F — площадь внутреннего сечения обсадной колонны). Этот способ называется «мгновенным подливом».
(где V0 — общий объем погружаемых под уровень баллонов; F — площадь внутреннего сечения обсадной колонны). Этот способ называется «мгновенным подливом».
|
|
|
Изменение уровня после подъема выражается величиной 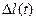 (рис. 7. 5).
(рис. 7. 5).
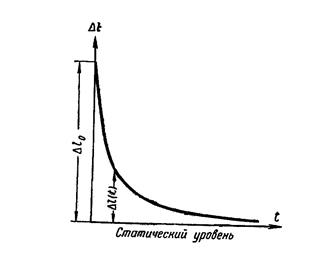
Рис. 7. 5. Снижение уровня в скважине после «мгновенного подлива».
При обработке результатов исследования кривая 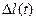 перестраивается в координатах
перестраивается в координатах 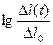 ,
,  в том же масштабе, что и палетка (рис. 7. 6). Фактическая кривая переносится на кальку и накладывается на палетку таким образом, чтобы горизонтальная линия фактической кривой
в том же масштабе, что и палетка (рис. 7. 6). Фактическая кривая переносится на кальку и накладывается на палетку таким образом, чтобы горизонтальная линия фактической кривой 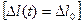 совпала с осью абсцисс палетки.
совпала с осью абсцисс палетки.
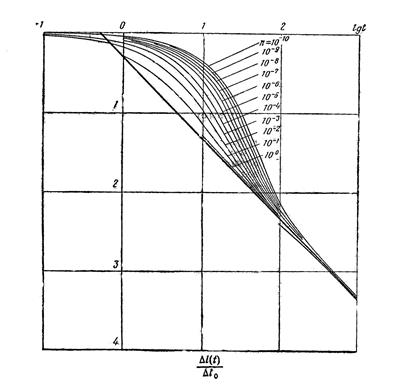 Рис. 7. 6. Палетка дли обработки результатов исследования скважин методом «мгновенного подлива». Параметром кривых является коэффициент п.
Рис. 7. 6. Палетка дли обработки результатов исследования скважин методом «мгновенного подлива». Параметром кривых является коэффициент п.
Добившись хорошего совпадения фактической кривой с одной из кривых палетки, с палетки на кальку переносится прямая, проходящая под углом 45° к оси  . В точке пересечения последней с осью ординат фактического графика получается значение
. В точке пересечения последней с осью ординат фактического графика получается значение 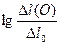 , по которому потенциированием находится значение
, по которому потенциированием находится значение 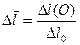 . Отмечается также величина параметра п кривой палетки, с которой совместилась фактическая кривая.
. Отмечается также величина параметра п кривой палетки, с которой совместилась фактическая кривая.
При исследовании скважины способом подкачки гидропроводность и приведенный радиус скважины определяются по формулам
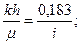 (7. 38)
(7. 38)
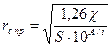 , (7. 39)
, (7. 39)
где i — уклон прямой в координатах 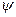 (S) к оси
(S) к оси  :
:
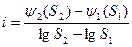 , (7. 40)
, (7. 40)
A, S — произвольная ордината на прямолинейной зависимости 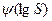 и соответствующее ей значение S.
и соответствующее ей значение S.
При исследовании скважин способом «мгновенного подлива» параметры пласта и скважины определяются по формулам
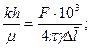 (7. 41)
(7. 41)
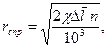 (7. 42)
(7. 42)
где 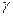 — относительная (безразмерная) плотность жидкости в скважине.
— относительная (безразмерная) плотность жидкости в скважине.
|
|
|


