 |
Тригонометрические функции. 4 глава
|
|
|
|
1) Защита от рассинхронизации. Несмотря на защитное смещение, сильная помеха может пробиться в линию без активных передатчиков и нарушить правильную последовательность приема посылок. Тогда возникает необходимость первой же нормальной посылкой вразумить принимающие устройства и не дать им принять помеху за посылку. Делается это с помощью синхронизации кадров (активная пауза) и синхронизации посылок (преамбула).
2) Контроль достоверности. Особо сильная помеха может вклиниться в посылку, исказить управляющие символы или данные в ней, а то и вовсе уничтожить ее. Кроме того, одно из подключенных к линии устройств (абонент) может выйти из строя и перестать отвечать на запросы. На случай такой беды существуют контрольная сумма, тайм-ауты и квитирование.
Контрольная сумма – в общем случае 1-2 байта кода, полученного некоторым преобразованием из данных посылки. Самое простое – "исключающее или" всем байтам данных. Контрольная сумма рассчитывается и включается в посылку перед отправкой. Принимающее устройство производит ту же операцию над принятыми данными и сверяет рассчитанную контрольную сумму с полученной. Если посылка была повреждена, то, скорее всего, они не совпадут. В случае применения ASCII протокола – код контрольной суммы также передается ASCII-символами.
Тайм-аут – максимальное время ожидания ответа от запрашиваемого устройства. Если посылка была повреждена или запрашиваемое устройство вышло из строя, то ведущее устройство не повиснет в ожидании ответа, а по истечении определенного времени признает наличие сбоя. После чего можно еще пару раз повторить запрос и, если сбой повторяется, перейти на отработку аварийной ситуации. Тайм-аут отсчитывается с момента завершения передачи запроса. Его длительность должна с небольшим запасом превышать максимальное время ответной передачи плюс время, необходимое на обработку запроса и формирование ответа. Ведомому устройству тоже не помешает отработка тайм-аутов. Особенно в ситуациях, когда отсутствие регулярного обновления данных или новых команд от ведущего устройства критично для работы устройств системы. Самая простая реализация для ведомого – сброс сторожевого таймера по приему посылки. Если по какой-либо причине данные перестали поступать – устройство сбросится по переполнению сторожевого таймера. После сброса устанавливается безопасный режим до приема первой команды.
|
|
|
Квитирование – подтверждение доставки (квитанция). Когда важно, чтобы ведомый обязательно получил данные или команду, возникает необходимость проконтролировать получение им посылки. Ведущее устройство, отправив ведомому данные, ждет ответа с подтверждением. Ведомое устройство, получив данные, в случае их корректности посылает ответ, подтверждающий доставку. Если по истечении тайм-аута ведущее устройство не получает подтверждение, делается вывод о сбое в связи или в ведомом устройстве. Дальше обычные меры – повтор посылки. Но тут есть нюанс: повреждена и не получена может быть сама квитанция. Ведущее устройство, не получив квитанцию, повторяет посылку, и ведомое отрабатывает ее повторно. Не всегда это существенно, но если перепосылалась команда типа "увеличить параметр на 1" это может привести к незапланированному двойному увеличению параметра. В таком случае надо предусмотреть что-нибудь типа циклической нумерации посылок, чтобы ведомое устройство отличало повторные посылки от новых и не отрабатывало их.
Лекция №4.
Тема: “Особенности ТОУ. АСУТП как система функциональных задач. Назначение алгоритмов контроля. Аналитическая градуировка и коррекция показаний датчиков. Фильтрация и сглаживание. Интерполяция и экстраполяция. Статистическая обработка экспериментальных данных. Контроль достоверности исходной информации”
|
|
|
4.1. Особенности ТОУ
Функциональные возможности практически любой системы управления (СУ) определяются особенностями объекта, для которого создается эта система. Для АСУТП объектом является технологический объект управления (ТОУ) С точки зрения материально-технической и организационной структур производства, а также характера протекания ТП, все многообразие ТОУ можно разделить на три составные группы: непрерывные, дискретные, непрерывно-дискретные. С точки зрения управления по виду уравнений связи между входными и выходными переменными ТОУ обычно классифицируют на одномерные и многомерные, линейные и нелинейные, с голономными и неголономными связями, сосредоточенными параметрами, на стационарные и нестационарные. Простейшими ТОУ являются одномерные, стационарные, сосредоточенные, линейные системы с голономными связями, более сложными - многомерные, нестационарные, нелинейные, с распределенными параметрами и с неголономными связями. Для объектов лесного комплекса характерны следующие особенности как объектов автоматизации:
– наличие разнородных функциональных задач, возникающих при автоматизации: контроль параметров технологических режимов, диагностика состояния и управления режимами ТОУ. Для класса непрерывных ТОУ характерны задачи стабилизации определенных переменных, а для периодических ТОУ типичны задачи программного регулирования;
– сравнительно высокий уровень автоматизации существующих ТОУ, определяемый локальными системами. Этот уровень позволяет в классе непрерывных ТОУ обеспечить стационарность их режимов, однако не гарантирует оптимальности с точки зрения технико-экономических показателей (ТЭП);
– повышение актуальности задачи оптимизации в целом. Обычно эта задача формулируется для получения основных и побочных продуктов ТП с наименьшими затратами при их качестве, регламентированном по ГОСТу, а также при наличии определенных технологических ограничений. Для ее решения локальной автоматики недостаточно и необходим системный подход, т.е. комплексная автоматизация. Она связана с усложнением схем управления и перехода к многоуровневым иерархическим САУ, а также с укрупнением оперативной информации о ТОУ (вычисление ТЭП, диагностических оценок, моделей ситуаций и т.д.);
|
|
|
– необходимость адаптации систем управления ТОУ к изменяющимся внешним и внутренним условиям (из-за изменения характеристик сырья в ТОУ; характеристик обрабатываемого материала в ТОУ или изменения характеристик оборудования ТОУ в связи с падением напряжения; наличие возмущений по нагрузке из-за включения-отключения параллельных станков и т.д.). Такая адаптация САУ может быть как локальной САУ (например, подстройкой параметров САР), так и глобальной, связанной с подстройкой уставок систем стабилизации, определяющих стационарный режим ТП и его оптимальность в целом;
– для класса непрерывных ТОУ достаточно, если локальные модели будут представлены в виде линеаризованных динамических характеристик каналов "управление -регулируемая переменная", "контролируемое возмущение - регулируемая переменная" (эти модели используются для синтеза локальных САР). Глобальные модели – в виде статических характеристик отдельных агрегатов ТОУ и выражения для критерия оптимальности в виде ТЭП технико-экономические показатели. Эти модели используются для оптимизации ТОУ в целом.
4.2 АСУТП как система функциональных задач
Анализ особенностей ТОУ, как объектов автоматизации, позволяет сформулировать положения, определяющие состав функциональных задач, которые должна решать АСУ ТП:
1. основные задачи управления ТОУ всегда формулируются как оптимизационные;
2. среди задач контроля и управления имеется определенная иерархичность.
Указанное, в итоге, определяет состав наиболее важных и часто встречающихся задач, которые должны решаться в соответствующих функциональных подсистемах АСУТП.

Рис.1 АСУТП как система функциональных задач
|
|
|
В системах АСУ ТП выделяется 5 классов типовых задач управления.
| Задачи АСУТП | Связь (алгоритм): | ||||
| С ЭВМ | С объектом | С документом | С оператором | С ЭВМ высшего порядка | |
| Первичная обработка информации | Организация сбора информации | Циклическая по группам, по приоритету | Нет | По вызову | |
| Определение статистических моментов | Разомкнутая периодическая | Вывод на печать | |||
| Оценка состояния | Разомкнутая постоянная | Вывод на печать | Прямая | ||
| Прогнозирование воздействий | Замкнутая периодическая | Есть индикация | Обратная | ||
| Статический контроль | Разомкнутая периодическая | Вывод на печать | |||
| Вычисление косвенных параметров | Разомкнутая периодическая | Вывод на печать | |||
| Определение функций распределения | Разомкнутая эпизодическая | Индикация | |||
| Идентификация (активные и пассивные методы | Алгоритмы генерирования сигналов | Разомкнутая эпизодическая | Есть | ||
| Определение статистической модели | Замкнутая, периодическая | Печать коэф-нта регрессии | Есть | Есть | |
| Определение динамич-ой модели харак-ик | Замкнутая, периодическая | Печать основных | Есть | ||
| Определение функций чувств-сти | Замкнутая, эпизодическая | Печать | Есть | ||
| Статист-ая оптимизация | Методы планирования эксперимента | Разомкнутая периодическая | Печать оптим-го режима | Есть | |
| Методы экстрем-го регулирования | Замкнутая, постоянная | ||||
| Адаптивные алгоритмы | Замкнутая, эпизодическая | Есть | |||
| Динамич-ая оптимизация | Програм-ное оптимальное управление | Разомкнутая постоянная | Ввод информ-и с носителя | Есть | |
| Управление с обратной связью | Замкнутая, постоянная | ||||
| Управление по возмущению | Замкнутая, постоянная | ||||
| Типовые алгоритмы регулирования П, ПИ, ПИД | Замкнутая, постоянная | ||||
| Компенсация возмущений | Замкнутая, постоянная | ||||
| Пуск, остановка | Разомкнутая разовая | Есть | |||
| Анализ аварийных ситуаций | Разомкнутая постоянная | Печать | Есть |
4.3 Назначение алгоритмов контроля
Алгоритмы централизованного контроля предназначены для сбора и передачи измерительной информации от датчиков, установленных на ТОУ, а также для первичной обработки этой информации с целью:
– определения текущих и прогнозируемых значений измеряемых величин и оценки неизмеряемых искомых величин по косвенным параметрам;
– вычисления учетных и технико-экономических величин по косвенным параметрам;
– обнаружения нарушений и неисправностей на производстве, требующих немедленного управления.
|
|
|
Результаты первичной обработки являются теми исходными данными, по которым рассчитываются все выходные параметры алгоритмов управления. Большинство результатов первичной обработки используется для оперативного формирования управляющих воздействий, поэтому соответствующие задачи первичной обработки должны решаться в реальном масштабе времени. Однако, некоторые показатели являются исходной информацией не в системе АСУТП, а передаются на более высокий уровень. Такая информация обычно обрабатывается в уменьшенном масштабе времени. Задача разработки алгоритмов контроля формируется следующим образом.
Заданы все исходные величины (в том числе показатели и события), которые должна определять подсистема контроля, и указаны требуемые параметры каждой выходной величины (точность ее определения, частота выдачи оператору или в другие подсистемы, форма выдачи и т.д.). Имеется совокупность измерительных средств, которая может быть использована в качестве источников исходной информации для определения заданных выходных величин. Требуется определить рациональный комплекс алгоритмов, перерабатывающий сигналы датчиков в искомые выходные величины и удовлетворяющий заданным требованиям на параметры выходных величин.
К задачам контроля относятся: линеаризация и коррекция, фильтрация и сглаживание сигналов датчиков, экстра- и интерполяция данных по дискретным замерам, контроль достоверности получаемой информации, вычисление различных статистических характеристик сигналов датчиков, оценка состояния объекта при наличии шумов измерений и доступных измерению ряда переменных, выявление аварийных ситуаций и диагностика в ТОУ, расчет ТЭП. После определения комплекса выходных величин, выданных подсистемой контроля, и установления совокупности измерительных средств, они могут быть использованы в качестве источников исходной информации на автоматизируемом объекте для разработки блок-схем переработки сигналов датчиков в искомые выходные величины подсистемы централизованного контроля. Для этого следует воспользоваться разделением всего процесса переработки измерительной информации на ряд последовательно выполняемых типовых операций. Последовательность выполнения операций следующая:
– аналитическая градуировка датчиков;
– экстра- и интерполяция дискретно измеряемых величин;
– контроль достоверности информации о процессе;
– определение суммарных и средних значений величин за заданные интервалы времени;
– коррекция динамической связи между измеряемой и искомой величиной и т.д.
Необходимо по каждой заданной выходной величине произвести набор операций, осуществляющих ее формирование из имеющихся измерительных сигналов, и указать последовательность выполнения этих операций. Рассмотрим кратко алгоритмы некоторых из перечисленных вычислительных операций.
4.4 Аналитическая градуировка и коррекция показаний датчиков
Значение выходного сигнала датчика y связано с измеряемой величиной x в общем случае монотонной зависимостью y = f (x). Для задач управления необходимо знать истинное значение измеряемой величины x, поэтому возникает необходимость вычислить x по значению показателя датчика y, т.е. нахождение функциональной зависимости x=f (y) = F−1(y).
Задача решается просто, если указанная зависимость линейная. В случае если функция F−1(y) является нелинейной, то используют либо метод линейной интерполяции табличного значения F(x) либо аппроксимацию функции F−1(y) при помощи степенного полинома
Pn(y). Для большинства датчиков механических и электрических величин, датчиков уровня и некоторых других характерна линейная зависимость: у = ах + в.
Если функция f(y) является нелинейной, можно выразить ее с помощью известных алгебраических и трансцендетных функций, однако этот путь довольно сложен и применяется редко. Обычно функция F(x) задается в табличном виде, например, по экспериментально снятым точкам в диапазоне предполагаемых измерений. Простейшим алгоритмом нахождения x при этом считается линейная интерполяция таблицы с заданным шагом.x. Недостатком такого алгоритма является большой объем памяти ЭВМ, т.к. необходимо запоминать всю таблицу. Поэтому наиболее удобным методом оказывается аппроксимация функции f(y) при помощи степенного полинома Pn(y) = a0 + a1y +….anyn.
При этом объем вычислений мал, а в памяти машины хранятся только n коэффициентов полинома (обычно n невелико). Для вычисления значений полинома в любой точке применяется схема Горнера, когда аппроксимация f(y) записывается в виде
Pn(y) = (((….(any + an-1)y + an-2)y +…. a1)y + a0.
Коэффициенты полинома ai (i = 0,1,…,n) заносятся в память машины в порядке убывания номеров их индексов.
Аппроксимацию табличных данных обычно проводят либо полиномом равномерного наилучшего приближения, либо с помощью полинома регрессии. В первом случае полученный полином дает минимальное значение максимальной ошибки линеаризации в диапазоне аппроксимации, во втором – минимальное значение среднеквадратической погрешности (при фиксированной степени полинома n). Для уменьшения времени вычислений и требуемой памяти ЦВМ желательно выбирать аппроксимирующий полином наименьшей степени, но обеспечивающий допустимую погрешность ∆xдоп. При аппроксимации полиномом равномерного наилучшего приближения должно выполняться требование [δi] ≤ δmax ≤ ∆xдоп.
Если аппроксимирующий полином есть, значения измеряемой величины вычисляются по схеме Горнера на основе показаний датчика; если аппроксимирующий полином не задан и в памяти ЦВМ записана вся градуировочная таблица, то расчет значений проводится по интерполяционной формуле.
В ряде АСУТП информация об измеряемых параметрах выражается в ЭВМ правильной дробью α, изменяющейся от 0 до 1 при изменении параметра от минимального до максимального значения. Тогда вычисление абсолютных величин давления, перемещения, объема, осуществляется по формуле: Pt = Pmaxα.
где Pt – текущее значение параметра; Pmax – максимальное значение шкалы датчика соответствующего параметра.
Преобразование температурных (параметров) сигналов производится по формуле:
θt = θmin + (θmax - θmin)α, где θmax, θmin – максимальное и минимальное значения шкалы датчика температуры (˚C).
4.5 Фильтрация и сглаживание
Задача фильтрации по Винеру формулируется следующим образом. Пусть входной сигнал представляет собой случайный процесс Z(t) при -∞ < t < ∞ и пусть Z(t) представляет собой смесь (не обязательно аддитивную) полезного сигнала y(t) и помехи ξ (t). Требуется построить систему (фильтр) такой обработки входного сигнала, которая позволила бы получить на выходе желаемый сигнал d(t), являющийся результатом определенной операции L над одним лишь полезным сигналом x(t): d(t) = L{x(t)}.
Обычно рассматривают следующие частные случаи:
а) d(t) = x(t)(-α) –задача фильтрации и сглаживания;
б) d(t) = x(t) – задача чистой фильтрации;
в) в(t) = y(t)(+α) – задача фильтрации и упреждения; где α >0.
При ξ (t) = 0 задачи (а) и (в) определяются как задачи чистого сглаживания и упреждения соответственно.
Существуют самые различные фильтры (Винера, Калмана, упрощенный фильтр Калмана, (α – β) фильтр и т.д.) отличающиеся своими характеристиками. Выбор фильтра определяется рядом противоречивых факторов (требованиями системы к точности объекта, относительной точностью фильтров, чувствительностью характеристик системы к изменению параметров модели, требованиями фильтров к вычислительным средствам и т.д.), поэтому исходят из компромиссного решения между точностью фильтра, его требованиями к вычислительным средствам и ограничениями системы.
С точки зрения требований к объему вычислений выгодно использовать фильтр экспоненциального сглаживания (ЭС): y(t) = γeγt, где γ – параметр фильтра.
Сравнение реализаций фильтра в непрерывном и дискретном варианте показало, что дискретный фильтр обладает практически большими преимуществами при использовании его в системе централизованного контроля. Сглаживание является частным случаем общей задачи фильтрации сигнала.
4.6 Интерполяция и экстраполяция
Интерполяция – построение приближенного или точного аналитического выражения функциональной зависимости, когда о ней известны только соотношения между аргументом и соответствующими значениями функции в конечном ряде точек имеет следующие применения в АСУТП:
– линеаризация и интерполяция сигналов датчиков;
– формирование непрерывно-изменяющегося сигнала по коэффициенту временного полинома или числовой программе в системах программного регулирования;
– получение аналитического выражения статической (обычно в виде квадратичной формы от входных воздействий) или динамической (обычно в виде дробно-рациональной передаточной функции) характеристик по экспериментально полученным точкам в задачах идентификации и характеризации;
– получение аналитического выражения корреляционных функций или спектральных плотностей при статистической обработки данных;
– переход от одной формы математического описания к другой в задачах характеризации;
– интерполяция таблиц, номограмм, диаграмм, хранящихся в памяти ЭВМ, для определения каких-либо параметров, например, параметров ПИД-регулятора по номограммам.
Для интерполирования функции по точным значениям применяют интерполяционные формулы:
– при линейной интерполяции значения функции f в точке (xi < x < xi+1) берется равным
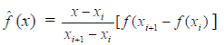
– при интерполировании по Лагранжу, когда известны значения функции в m точках x1…xm, образуется многочлен степени (m – 1):

Задача интерполяции при наличии помех измерений называется задачей сглаживания.
Экстраполяция – полученных из наблюдений над одной частью явления на другую его часть, недоступную для наблюдения. Имеет следующее применение в АСУТП:
– повышение качества управления (быстродействия, устойчивости и т.п.), обычно – за счет введения в закон управления производных;
– предсказание (прогнозирование) возмущающих воздействий или возмущающего движения при создании оптимальных систем комбинированного типа, содержащих две составляющих управления, из которых одна является функцией текущего состояния, а вторая – функцией предсказанного возмущения;
– предсказание положения в стационарной точке в задачах планирования экстремальных экспериментов или экстремального регулирования для ускорения процесса поиска;
– предсказание аварийных ситуаций и редко измеряемых переменных, когда для управления процессом требуется более частый опрос переменных, чем реально возможный.
В большинстве случаев предсказание можно осуществлять и без построения временной модели переменной. Применяют следующие алгоритмы предсказания – ступенчатую аппроксимацию, когда предсказываемое значение переменной совпадает с ее величиной (при сглаженной помехе) в последней точке замера (этот метод не требует никаких вычислений, однако его погрешность максимальна по сравнению с другими алгоритмами.
4.7 Статистическая обработка экспериментальных данных
Важным моментом задачи исследования и управления ТОУ является обработка большого потока экспериментальной информации, имеющей, как правило, случайный характер. И это обуславливает необходимость использования методов математической статистки для извлечения ценной информации из экспериментальных данных. С учетом необходимости работы АСУТП в реальном масштабе времени, статистическая обработка информации должна быть оперативной. То есть обработка должна осуществляться в ходе эксперимента в темпе поступления информации непосредственно от исследуемых объектов за минимальное время и с получением результатов обработки в виде, удобном для дальнейшего использования. В связи с этим для обеспечения оперативности обработки экспериментальной информации должны использоваться простые методы и алгоритмы статистической обработки. Целью оперативной статистической обработки экспериментальной информации в рамках анализа реализаций случайных процессов является получение системы статистических оценок с определенной доверительной вероятностью и точностью в реальном масштабе времени.
Оценки плотностей вероятностей эмпирических распределений в виде многомерного функционала при условии стационарности и эргодичности случайных процессов x1(t),x2(t) – является исчерпывающей характеристикой совокупности процессов {xk(t)}.
Это дает возможность в рамках корреляционно-регрессионного анализа получить функции корреляции, дисперсий, спектральных плотностей, безусловных и условных математических ожиданий и других числовых характеристик, связанных с физическими параметрами объекта, а также ошибки (дисперсии или СКО), спектральные характеристики и т.д., по которым можно судить о качественном состоянии объекта.
Ниже перечислены некоторые алгоритмы статистической обработки экспериментальной информации: методы определения функций распределения, методы определения математического ожидания, методы определения функций корреляции
4.8 Контроль достоверности исходной информации
Назначение алгоритмов контроля достоверности исходной информации – повысить точность и надежность работы АСУТП. Точность работы отдельных датчиков может быть несколько улучшена при одновременном контроле ряда параметров технологического процесса за счет рационального использования информации, поступающей от других датчиков объекта, либо за счет информации, хранимой в памяти ЦВМ. При этом рациональное корректирование работы отдельных датчиков позволяет значительно повысить достоверность информации, выдаваемой ЦВМ операторам.
Рассмотрим некоторые методы решения такой задачи. Возможность повышения точности определения измеряемой величины появляется при ее одновременном замере несколькими датчиками, либо замере и одновременно возможности ее вычисления (на основе математической модели) по исходным данным, получаемым от других датчиков. Распространенными примерами таких ситуаций являются замеры расходов материальных потоков или энергетических потоков в начале и конце трубопровода; замер расхода вещества датчиком и одновременное вычисление его из уравнения баланса для узла, потребляющего или выделяющего данное вещество; непосредственное измерение искомой величины рядом датчиков, резервирующих друг друга и т.д.
Использование математической модели позволяет либо обнаружить и скорректировать источник недостоверной информации (неисправный датчик), либо установить нарушение математической модели, что может служить сигналом об аварийной ситуации, например, разрушение трубопровода.
Пусть x{x1, x2,..., xn} – вектор расхода n потоков на производстве, которые связаны m(m<n) уравнениями материального баланса:

где aij – параметры уравнений.
Частично или полностью эти потоки измеряются соответствующими расходомерами, которые выдают значения расходов с погрешностями  . При этом каждый датчик имеет свою известную среднюю квадратичную погрешность оценки σx{σx1,....,σxm}. Естественно, за счет этих погрешностей на практике уравнения баланса удовлетворяются неточно. Это позволяет поставить задачу повышения достоверности работы датчиков расхода за счет использования дополнительной информации, содержайщеся в уравнениях баланса.
. При этом каждый датчик имеет свою известную среднюю квадратичную погрешность оценки σx{σx1,....,σxm}. Естественно, за счет этих погрешностей на практике уравнения баланса удовлетворяются неточно. Это позволяет поставить задачу повышения достоверности работы датчиков расхода за счет использования дополнительной информации, содержайщеся в уравнениях баланса.
Корректировка величин потоков заключается в определении такого вектора x, который удовлетворял бы уравнению материального баланса и минимизировал бы квадратичную ошибку отклонения от измеренного значения:

Поставленная задача является задачей математического программирования и может быть решена методом неопределенных множителей Лагранжа.
Еще одним случаем появления избыточной информации является наличие в технологических процессах нескольких конструктивно идентичных параллельных технологических ниток, оснащенных одинаковыми измерительными приборами и работающих в одинаковом режиме. Параметры состояния ниток, замеренные в их конструктивно идентичных точках, близки по значению. Здесь, как и в приведенных выше двух других случаях (дублирование замеров особо важных технологических параметров и проверка показаний датчиков методом косвенного измерения, с использованием математических моделей отдельных технологических узлов), имеется избыточная информация. Ее требуется использовать для оценки надежности источника контролируемой величины и выбора наиболее достоверного значения или для присвоения контролируемой переменной заданного заменяющего значения, если все три анализируемых значения будут признаны недостоверными. Эта задача обычно решается с помощью следующего алгоритма контроля достоверности информации:
|
|
|


