 |
Внимание! Массы Луны, Харона и Титана считайте пренебрежимо малыми по сравнению с массами планет
|
|
|
|
Внимание! Массы Луны, Харона и Титана считайте пренебрежимо малыми по сравнению с массами планет
6. Сделайте вывод о проделанной работе.
Практическая работа № 5
Тема: Определение расстояний и размеров тел в Солнечной системе.
Цель: Познакомиться с методами определения расстояний и размеров тел в Солнечной системе и научиться их практически рассчитывать.
Теория:
1. Определение расстояний по параллаксам светил. Допустим, что из точки А нужно определить расстояние до недоступной точки С (рис. 24). Для этого прежде всего тщательно измеряется расстояние до какой-нибудь доступной точки В. Отрезок АВ называется базисом. Далее из точек А и В угломерным геодезическим инструментом измеряют CAB и АВС. Таким образом, в треугольнике ABC известны углы и сторона АВ = с. Остальные элементы косоугольного треугольника ABC можно вычислить по формулам тригонометрии.
2.
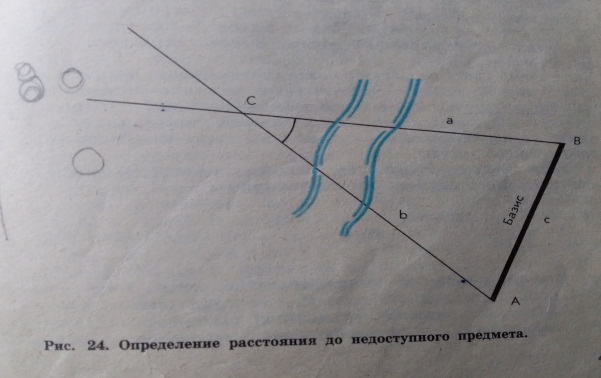
Рис. 24. Определение расстояния до
недоступного предмета Рис. 25. Горизонтальный параллакс светила.
УголАСВ, под которым из недоступного места виден базис, называется параллаксом. При данном расстоянии до предмета параллакс тем больше, чем больше базис.
В пределах Солнечной системы в качестве базиса используют экваториальный радиус Земли. Рассмотрим прямоугольный треугольник (рис. 25), вершинами которого являются центр светила О1, центр Земли О и точка, изображающая местоположение наблюдателя К. Как следует из чертежа, наблюдатель видит светило на горизонте. Угол р0, под которым со светила, находящегося на горизонте, был бы виден экваториальный радиус Земли, называется горизонтальным экваториальным параллаксом светила. Конечно, со светила никто не наблюдает радиус Земли, а горизонтальный параллакс определяют по измерениям высоты светила в момент верхней кульминации из двух точек земной поверхности, находящихся на одном географическом меридиане и имеющих известные географические широты.
|
|
|
Если горизонтальный параллакс (р0) найден, то расстояние до светила вычисляется по формуле:
(19)
где D — расстояние от центра Земли до центра какого-нибудь тела Солнечной системы;
— экваториальный радиус Земли; р0 — горизонтальный параллакс светила.
Наибольший горизонтальный параллакс имеет ближайшее к Земле небесное тело — Луна (p( = 57'02′ ). Параллаксы планет и Солнца составляют всего лишь несколько секунд дуги
( 
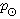= 8, 79′ ) Поскольку углы р0 малы, то их синусы можно заменить самими углами, т. е. sin р0 ≈ р0, если величина угла выражена в радианах. Но р0 обычно выражено в секундах дуги, поэтому 
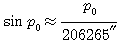; так как 1 радиан = 57, 3° = 3438' = 206265′. Учитывая это, формулу (19) можно записать в виде:
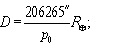(20)
здесь р0 выражено в секундах дуги, а D в зависимости от — либо в километрах
(если — в километрах), либо в радиусах Земли.
Пример 6. Зная горизонтальный параллакс Луны и экваториальный радиус Земли (6378 км), найти расстояние от Земли до Луны.
|
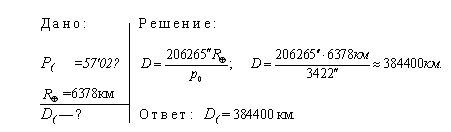
2. Радиолокационный метод. Он заключается в том, что на небесное тело посылают мощный кратковременный импульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: с = 299792458 м/с. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние. Идея непосредственного метода определения расстояния до небесных тел (в частности, расстояния между Землей и Луной) была обоснована отечественными физиками Л. И. Мандельштамом и Н. Д. Папалекси.
|
|
|
Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера.
Для космических полетов необходимо с большой точностью определять значение астрономической единицы. Еще сравнительно недавно астрономическая единица была известна с точностью до нескольких десятков тысяч километров. Из радиолокационных наблюдений Венеры получено следующее значение астрономической единицы:
|
|
|
