Построение, преобразование и обработка матриц

 

1 В данной действительной матрице размера n*m поменять местами строку, содержащую элемент с наибольшим значением, со строкой, содержащей элемент с наименьшим значением. Предполагается, что эти элементы единственны.

 

2 В данной действительной квадратной матрице порядка n найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.

 

3 Все элементы с наибольшим значением в данной целочисленной матрице порядка 10 заменить нулями.

 

4 Дана действительная матрица размера n*m. Найти среднее арифметическое ее наибольшего и наименьшего значений.

 

5 Дана действительная матрица размера n*m, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по модулю элемент.

 

6 Расстояние между k и e строками матрицы определяется как:

Вычислить расстояния от первой до остальных строк матрицы.

 

7 Расстояние между 1-ым столбцом и k определяется как:

Вычислить расстояние от первого до остальных столбцов матрицы.

 

8 Характеристикой строки целочисленной матрицы назовем сумму ее положительных четных элементов. Определить номер строки с наибольшей характеристикой.

 

9 Характеристикой строки целочисленной матрицы назовем сумму ее отрицательных нечетных элементов. Определить номер строки с наименьшей характеристикой.

 

10 Характеристикой столбца матрицы назовем произведение положительных элементов с четными номерами строк. Упорядочить столбцы матрицы по возрастанию их характеристик.

 

11 Характеристикой столбца целочисленной матрицы назовем сумму элементов, являющихся простыми числами. Упорядочить столбцы матрицы по убыванию их характеристик.

 

12 Характеристикой строки назовем наибольшее количество идущих подряд нулей. Упорядочить строки матрицы по возрастанию их характеристик.

 

13 Характеристикой столбца назовем наибольшее количество идущих подряд отрицательных элементов. Упорядочить столбцы матрицы по убыванию их характеристик.

 

14 Характеристикой строки целочисленной матрицы назовем длину, содержащейся в ней максимальной серии. Для каждой строки напечатать ее характеристику.

 

15 Дана символьная матрица, каждая строка которой является предложением. Для каждой строки определить количество слов.

 

16 Дана символьная матрица. Упорядочить строки матрицы по алфавиту.

 

17 Дана символьная матрица. Упорядочить строки матрицы в соответствии с ростом доли цифр.

 

18 Дана символьная матрица. Характеристикой строки назовем длину, содержащейся в ней максимальной серии. Определить номер строки, имеющей наибольшую характеристику.

 

19 Дана символьная матрица, каждая строка которой является предложением. Характеристикой предложения назовем длину самого длинного слова. Определить номер строки, имеющей наименьшую характеристику.

 

20 Дана символьная матрица. Для каждой строки определить количество различных латинских букв (большие и малые не различать).

 

21 Дана символьная матрица. Расстоянием между двумя строками назовем количество позиций, в которых различаются эти строки. Для каждой строки вычислить расстояние от нее до первой.

 

22 Дана целочисленная матрица. Для каждого столбца вычислить количество полных квадратов. Определить номер столбца, для которого эта характеристика имеет наибольшее значение.

 

23 Дана целочисленная матрица. Для каждого столбца матрицы вычислить количество элементов, являющихся удвоенными нечетными числами. Определить, будут ли упорядочены полученные значения.

 

24 Дана символьная матрица (латинский алфавит). Для каждой строки определить длину содержащейся в ней максимальной серии символов, отличных от букв.

 

25 Дана целочисленная матрица. Для каждого столбца определить сколько раз в нем меняется знак. Упорядочить столбцы по убыванию указанных характеристик. Серия - последовательность, составленная из совпадающих элементов.

 

26 Дана действительная матрица размера 10х9. Определить числа b₁, b₂,..., b₁₀, равные значениям средних арифметических элементов строк.

 

27 Дана действительная матрица размера n на m. Получить последовательность b₁, b₂,..., b_n, где b_k-это произведение квадратов тех элементов k-ой строки, модули которых принадлежат отрезку [1,1.5].

 

28 Характеристикой столбца целочисленной матрицы назовем произведение положительных нечетных элементов. Указать номер столбца с минимальной характеристикой.

 

29 Дана матрица A(nxm). Вычислить , где x_i-сумма положительных элементов i-ой строки.

 

30 Даны целочисленные матрицы C(5x5) и D(5x5). Построить x₁,... x₅, где x_i =1, если i-ые строки 1-ой и 2-ой матриц содержат не более 3-х четных элементов.

 

 

Лабораторная работа №8

Процедуры

 

1 Даны целочисленные матрицы A(6x6) и B(6x6). Построить 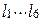, где -равно 1, если все элементы i-х строк 1-ой и 2-ой матриц отрицательны, иначе -равно 0.

 

2 Даны две действительные квадратные матрицы порядка m. Построить

последовательность из нулей и единиц b₁,..., b_n, где b_i =1, если элементы i-ой строки матрицы образуют возрастающую последовательность и b_i =0 в противном случае.

 

3 Даны натуральное число n, действительное число x и две действительные матрицы размера nx2n. Получить последовательность b₁,..., b_n из нулей и единиц, где b_i =1, если элементы i-ой строки матрицы не превосходят x и b_i =0 в противном случае.

 

4 Напечатать особые элементы матриц C(nxm) и В(n,2m). Элемент

называется 'особым', если он больше суммы остальных элементов своего столбца.

 

5 Определить количество 'особых' элементов матрицы A(nxm), B(nxm)

принадлежащих главной диагонали. Элемент называется 'особым' если в строке слева от него находятся меньшие, а справа большие элементы.

 

6 Даны две целочисленные квадратные матрицы порядка 15. Выяснить, имеются ли в матрицах ненулевые элементы. Если имеются, то указать индексы всех ненулевых элементов.

 

7 Даны целые числа a₁,..., a₁₀ и две целочисленных квадратных матрицы А(nxn) и B(nxn).

Заменить нулями в матрицах те элементы с четной суммой индексов, для которых имеются равные среди a₁,..., a₁₀.

 

8 Даны действительные матрицы размера А(18 x n) и В(15 x n). Найти значение наибольшего по модулю элемента матрицы, а также индексы какого-нибудь элемента с найденным значением модуля.

 

9 Даны две квадратные матрицы A(nxn) и B(mxm). Найти наибольшее и наименьшее значение

среди элементов, расположенных в заштрихованной части матрицы

 

10 Даны A и С квадратные матрицы порядка n. Получить вектор Ab и Сb, где b-вектор,

элементы которого вычисляются по формуле

 

; ;

 

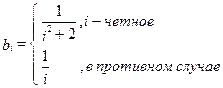11 Даны две действительные матрицы порядка (nxn). Получить новую

матрицу умножением элементов каждой строки 1-ой матрицы на наибольшее из значений элементов соответствующей строки второй матрицы.

 

12 В данных действительных квадратных матрицах порядка n найти сумму

элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.

 

13 Даны две действительные квадратные матрицы порядка 10 и12. В строках с отрицательным элементом на главной диагонали найти сумму всех элементов.

 

14 Даны две действительные матрицы размера nxm и nхk. Определить числа b₁,..., b_n, для каждой матрицы равные произведениям отрицательных элементов строк.

 

15 Даны натуральное число n, и две действительные квадратные матрицы порядка n.

Построить последовательность b₁,..., b_n для каждой матрицы, состоящую из нулей и единиц, в которой b_i=1 тогда и только тогда, когда в i-ом столбце матрицы есть хотя бы один отрицательный элемент.

 

16 Даны две действительные матрицы размера mxn и mxk. Определить для каждой матрицы числа b₁,..., b_m, равные наибольшим значениям элементов строк.

 

17 Даны две действительные квадратные матрицы порядка n. Получить для каждой матрицы

где x_i-наибольшее значение элементов i-ой строки.

 

18 Даны две целочисленные квадратные матрицы порядка 6. Построить b₁,...,

b₆, где b_i =1, если все элементы i-ой строки 1-ой матрицы больше соответствующих элементов i-ой строки 2-ой матрицы, иначе 0.

 

19 Даны две действительные квадратные матрицы порядка n. Получить для каждой матрицы

S = b₁ + b₂ +...+ b_n,

где b_i -наибольшее значение из элементов i-ой строки.

 

20 Даны две действительные матрицы размера nxm и nхk. Построить для каждой последовательность b₁,..., b_n по следующему правилу: если первый элемент i-ой строки матрицы отрицательный, то b_i равно сумме элементов строки, иначе - нулю.

 

21 Даны натуральное число n, две действительные квадратные матрицы порядка n. Построить последовательность b₁,..., b_n для каждой матрицы состоящую из нулей и единиц, в которой b_i=1 тогда и только тогда, когда в i-ой строке матрицы есть хотя бы один элемент отличный от 0.

22 Даны матрицы A(10x11) и В(10,15). Определить k₁,..., k₁₀ для каждой матрицы, равные количеству положительных элементов в соответствующей строке.

23 Даны две целочисленные квадратные матрицы порядка 10 и 12. Найти для каждой номера столбцов, все элементы которых принадлежат отрезку [0,5].

24 Даны две действительные квадратные матрицы порядка 10 и 20. В строках с отрицательным элементом на главной диагонали найти произведение всех элементов.

25 Даны две целочисленные квадратные матрицы порядка 6. Построить a₁,...,

a₆, где a_i=1, если количества отрицательных и неотрицательных элементов в i-ых строках обоих матриц совпадают, иначе 0.

26 Даны две целочисленные квадратные матрицы порядка n и m. Найти для каждой номера строк, все элементы которых нули.

 

 

Лабораторная работа №9.

Строковый тип

1.Дана последовательность, содержащая от 2 до 30 слов, в каждом из которых от 2 до 10 латинских букв; между соседними словами - не менее одного пробела, за последним словом точка. Напечатать все слова, отличные от последнего слова, предварительно преобразовав каждое из них по следующему правилу:

- перенести первую букву в конец слова;

2. Условие задачи 1:

-удалить из слова первую букву;

3.Условие задачи 1:

-удалить из слова последнюю букву;

4.Условие задачи 1:

-удалить из слова все последующие вхождения первой буквы;

5. Условие задачи 1:

- удалить из слова все предыдущие вхождения последней буквы;

6. Условие задачи 1:

-оставить в слове только первые вхождения каждой буквы;

7. Условие задачи 1:

-если слово нечетной длины, то удалить его среднюю букву.

 

8.Дана последовательность, содержащая от 2 до 50 слов, в каждом из которых от 1 до 8 строчных латинских букв; между соседними словами - не менее одного пробела, за последним словом - точка. Напечатать те слова последовательности, которые отличны от последнего слова и удовлетворяют следующему свойству:

- слово симметрично;

9. Условие задачи 8:

-буквы слова упорядочены по алфавиту;

10. Условие задачи 8:

-слово совпадает с начальным отрезком латинского алфавита (a, ab, abc, т.д.); учесть, что в диапазоне 'a'..'z' могут быть литеры, отличные от латинских букв;

11.Условие задачи 8:

-слово совпадает с конечным отрезком латинского алфавита (z, yz, xyz и т.д.);

12. Условие задачи 8:

-в слове нет повторяющихся букв;

13. Условие задачи 8:

-каждая буква входит в слово не менее 2-х раз;

14. Условие задачи 8:

-в слове гласные буквы (a,e,i,o,u) чередуются с согласными.

 

15.Даны натуральное число n, символы S₁,... S_n. Будем рассматривать слова,

образованные символами, входящими в последовательность S₁,... S_n группы символов, разделенные одним или несколькими пробелами, назовем словами.

-Удалить все слова с нечетными порядковыми номерами и перевернуть слова с четными номерами.

16. Условие задачи 1:

-Удалить из S₁,... S_n все слова, в которых встречается не более 2-х различных букв.

17. Условие задачи 1:

-Удалить из S₁,... S_n все слова, оканчивающиеся группой букв, "кая"

или "кое".

 

18. Даны натуральное число n, символы S₁,... S_n. Заменить в

последовательности каждую группу "child" словом "children".

 

19.Даны натуральное число n, символы S₁,... S_n. Исключить из

последовательности группы символов, расположенные между скобками (,). Сами скобки тоже должны быть исключены.

Предполагается, что внутри каждой пары скобок нет других скобок.

 

20.Даны натуральное число n, символы S₁,... S_n. Группы символов, разделенные пробелами, будем называть словами. Преобразовать данную последовательность, заменяя всякое вхождение слова "это" на слово "то".

 

21.Даны символы S₁,... S_n. Известно, что символ S₁ отличен от пробела и что среди S₁, S₂,... имеется хотя один пробел. Рассматриваются S₁,... S_n - символы, предшествующие первому пробелу (n заранее неизвестно). Преобразовать последовательность.

- Удалить из нее все символы, не являющиеся буквами (латинскими).

 

22. Условие задачи 21:

-Заменить все малые буквы одноименными большими.

 

23. Условие задачи 21:

-Удалить все символьные являющиеся буквами или цифрами, и заменить каждую большую букву одноименной малой.

 

24. Условие задачи 21:

-Удалить из каждой группы идущих подряд цифр, в которой более 2-х цифр и которой предшествует точка, все цифры, начиная с третьей (например, ab + 0.1973 -1.1 в ab+0.19-1.1).

 

25. Условие задачи 21:

-удалить из каждой группы цифр, которой не предшествует точка, все начальные нули (кроме последнего, если за ним идет точка).

 

26.Дан текст из 60 литер. Напечатать этот текст, подчеркивая (ставя минусы в соответствующих позициях следующей строки) все входящие в него заглавные и строчные русские буквы.

 

27.Дана строка литер (n<255). Заменить все вхождения "ph" на "f", а все вхождения "ed" на "inq".

 

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: