 |
Уравнение гармонических колебаний
|
|
|
|
 ,
,
где x – смещение точки от положения равновесия; A – амплитуда колебаний ( = xmax);
= xmax);  – циклическая частота колебаний; t– время;
– циклическая частота колебаний; t– время;  – начальная фаза колебаний;
– начальная фаза колебаний; 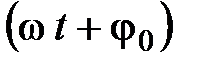 – фаза колебаний в момент времени t.
– фаза колебаний в момент времени t.
2. Циклическая частота колебаний

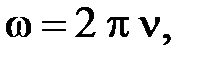
где T – период колебаний;  – частота колебаний.
– частота колебаний.
3. Скорость и ускорение колеблющейся материальной точки

 .
.
4. Сила, под действием которой материальная точка массой m совершает колебания:

или

где 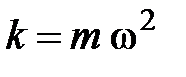 – коэффициент упругости; Fx – квазиупругая сила.
– коэффициент упругости; Fx – квазиупругая сила.
5. Полная энергия материальной точки, совершающей гармонические колебания:

6. Период колебаний гармонического осциллятора:
1) физического маятника

где I – момент инерции колеблющегося тела относительно оси колебаний; b – расстояние от центра масс тела до оси колебаний; g – ускорение свободного падения;  – приведённая длина физического маятника;
– приведённая длина физического маятника;
2) математического маятника

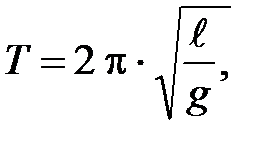
где  – длина маятника;
– длина маятника;
3) пружинного маятника (тела, подвешенного на пружине, масса которой мала по сравнению с массой тела)

где m – масса тела; k – жесткость пружины;
4) идеального колебательного контура
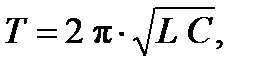
где L – индуктивность контура; С – электроёмкость контура.
7. Координаты центра масс системы материальных точек

где  – координаты
– координаты  материальной точки массой
материальной точки массой  .
.
8. При сложении двух одинаково направленных гармонических колебаний одинаковой частоты получается гармоническое колебание того же периода с амплитудой

и начальной фазой
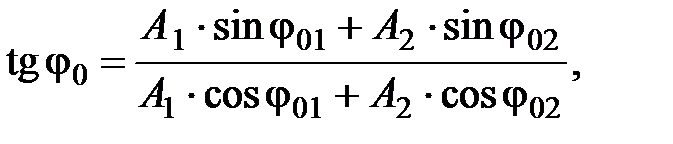
где  – амплитуды складываемых колебаний;
– амплитуды складываемых колебаний;  – начальные фазы (разность фаз в любой момент времени равна разности начальных фаз).
– начальные фазы (разность фаз в любой момент времени равна разности начальных фаз).
9. При сложении двух взаимно перпендикулярных колебаний одинаковой частоты уравнение траектории результирующего движения в координатах x, y имеет вид
|
|
|
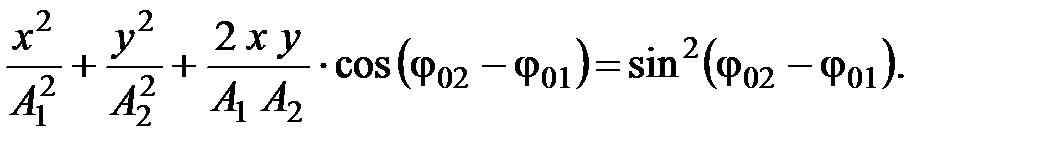
В частных случаях:
а)  если
если 
б)  если
если 
в)  если
если 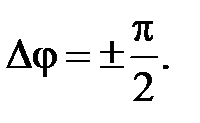

10. Дифференциальное уравнение свободных незатухающих гармонических колебаний материальной точки

где  – вторая производная смещения по времени (физический смысл – ускорение).
– вторая производная смещения по времени (физический смысл – ускорение).
Решение этого уравнения

где  – собственная циклическая частота колебаний (
– собственная циклическая частота колебаний ( ).
).
11. Дифференциальное уравнение затухающих колебаний

где  – коэффициент затухания (
– коэффициент затухания (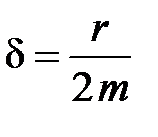 ); r – коэффициент сопротивления;
); r – коэффициент сопротивления;  – собственная циклическая частота колебаний (
– собственная циклическая частота колебаний ( ).
).
Решение этого уравнения

где 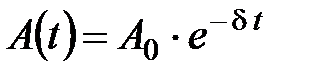 – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний;  – амплитуда колебаний в момент времени
– амплитуда колебаний в момент времени 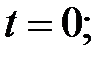
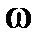 – циклическая частота затухающих колебаний (
– циклическая частота затухающих колебаний (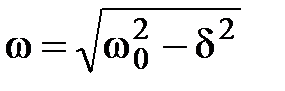 ).
).
12. Логарифмический декремент затухания

где 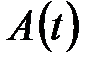 и
и  – амплитуды двух последующих колебаний, отстоящих по времени друг от друга на период.
– амплитуды двух последующих колебаний, отстоящих по времени друг от друга на период.
13. Дифференциальное уравнение вынужденных колебаний


где 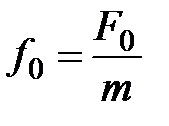 ;
;  – амплитудное значение внешней вынуждающей силы
– амплитудное значение внешней вынуждающей силы  ;
; 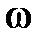 – циклическая частота колебаний вынуждающей силы.
– циклическая частота колебаний вынуждающей силы.
Решение этого уравнения для области установившихся колебаний

где А – амплитуда вынужденных колебаний
 ;
;
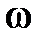 – циклическая частота вынужденных колебаний, равная частоте колебаний внешней силы;
– циклическая частота вынужденных колебаний, равная частоте колебаний внешней силы;  – величина отставания фазы вынужденных колебаний от фазы колебаний внешней силы
– величина отставания фазы вынужденных колебаний от фазы колебаний внешней силы
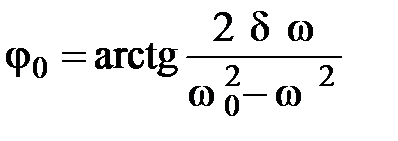 .
.
14. Резонансная частота и резонансная амплитуда:


ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 17. Материальная точка массой  г совершает гармонические колебания с частотой
г совершает гармонические колебания с частотой  Гц. Амплитуда колебаний
Гц. Амплитуда колебаний  см. Определить: 1) максимальную силу, действующую на материальную точку; 2) полную энергию колеблющейся точки.
см. Определить: 1) максимальную силу, действующую на материальную точку; 2) полную энергию колеблющейся точки.
Дано: 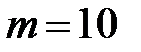 г =
г =  кг;
кг; 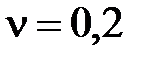 Гц;
Гц; 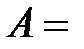 5 см = 0,05 м.
5 см = 0,05 м.
Найти: 
Решение.
Уравнение гармонических колебаний
 .
.
Сила, действующая на материальную точку, по второму закону Ньютона

где  – ускорение материальной точки.
– ускорение материальной точки.
Сила будет максимальна при условии, когда  Тогда
Тогда 
Так как 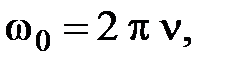 (1)
(1)
то

Выполним вычисления
|
|
|
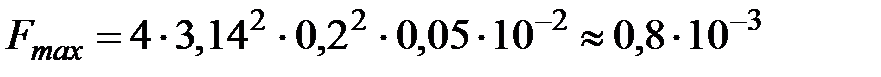 Н.
Н.
Полная энергия колеблющейся точки
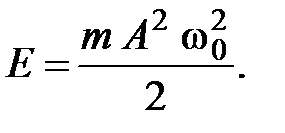 (2)
(2)
Подставим (1) в (2)

Выполним вычисления
 Дж.
Дж.
Ответ:  0,8 мН;
0,8 мН;  19,7 мкДж.
19,7 мкДж.
Пример 18. Складываются два колебания одинакового направления.
Уравнения этих колебаний  ,
, 
где 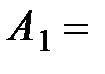 1 см,
1 см,  2 см,
2 см, 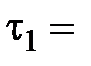 1/6 с,
1/6 с, 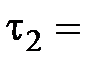 1/2 с,
1/2 с,  Определить: 1) начальные фазы исходных колебаний; 2) амплитуду и начальную фазу результирующего колебания.
Определить: 1) начальные фазы исходных колебаний; 2) амплитуду и начальную фазу результирующего колебания.
Дано:  ;
;  ;
;
 1 см = 0,01 м;
1 см = 0,01 м;  2 см = 0,02 м;
2 см = 0,02 м;  1/6 с;
1/6 с;  1/2 с;
1/2 с; 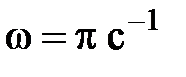 .
.
Найти:  ;
; 
Решение.
Уравнение гармонического колебания имеет вид
 (1)
(1)
Запишем уравнения исходных колебаний
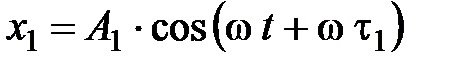 , (2)
, (2)
 . (3)
. (3)
Сравнив (2) и (3) с (1), видим, что

Выполним вычисления

Для определения  и
и  результирующего колебания построим векторную диаграмму (рис. 52).
результирующего колебания построим векторную диаграмму (рис. 52).
| X |
| Y |

|

|

|

|

|
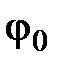
|
Рис. 52
Амплитуда результирующего колебания является диагональю параллелограмма, построенного на векторах 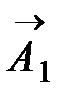 и
и 
По теореме косинусов
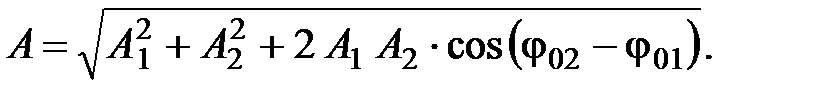
Выполним вычисление амплитуды результирующего колебания
 м.
м.
Так как

то

Выполним вычисления начальной фазы результирующего колебания
 рад.
рад.
Так как частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту, и уравнение этого колебания будет иметь вид

Ответ:  м;
м;  рад.
рад.
Пример 19. Найти число N полных колебаний системы, в течение которых энергия системы уменьшилась в 2 раза. Логарифмический декремент затухания 
Дано:  ;
;  .
.
Найти: N.
Решение. Полная энергия колебательной системы складывается из потенциальной и кинетической
 . (1)
. (1)
После подстановки в выражение (1) формул  и
и  , соответствующих затухающим колебаниям, получим зависимость энергии от времени
, соответствующих затухающим колебаниям, получим зависимость энергии от времени  .
.
При малом затухании ( ) зависимость
) зависимость  становится практически экспоненциальной
становится практически экспоненциальной
 .
.
Запишем значения энергии для двух моментов времени и найдём отношение энергий
 ;
;  ;
;
 ,
,
где  – время, за которое энергия системы уменьшается в 2 раза.
– время, за которое энергия системы уменьшается в 2 раза.
Так как  , то
, то
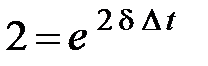 .
.
Прологарифмируем это выражение
 . (2)
. (2)
Выразим время 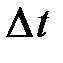 через период Т колебаний
через период Т колебаний
 . (3)
. (3)
После подстановки выражения (3) в (2), получим
 .
.
Так как  ,
,
то  .
.
Тогда  .
.
Выполним вычисления
 .
.
Ответ: N = 34.
3.2 ВОЛНЫ. ВОЛНОВАЯ ОПТИКА
Основные законы и формулы
1. Длина волны определяется по формуле
l = u T = u/n,
где u - скорость волны, м/c; n - частота колебаний точек упругой среды, в которой распространяется волновой процесс, Гц.
|
|
|
2. Уравнение волны в среде без поглощения:
- плоской, распространяющейся вдоль положительного направления оси  :
:
 ;
;
- сферической:
 ,
,
где  – круговая (циклическая) частота,
– круговая (циклическая) частота,  – волновое число,
– волновое число,  – длина волны,
– длина волны,  – расстояние от центра волны до рассматриваемой точки среды.
– расстояние от центра волны до рассматриваемой точки среды.
2. Плотность потока энергии – вектор Умова (в зарубежной литературе – вектор Пойтинга):
 ,
, 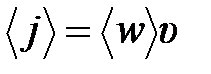 ,
,
где 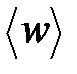 – среднее значение объемной плотности энергии,
– среднее значение объемной плотности энергии,  – круговая (циклическая) частота.
– круговая (циклическая) частота.
3. Интенсивность волны  – величина, определяемая средней по времени энергией, переносимой волной за единицу времени через единицу площади, перпендикулярной направлению распространения волны:
– величина, определяемая средней по времени энергией, переносимой волной за единицу времени через единицу площади, перпендикулярной направлению распространения волны: 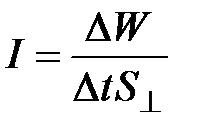 .
.
 ,
,
энергия, содержащаяся в объеме  , за время
, за время 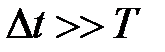 (
( – период колебаний энергии) пройдет через поверхность
– период колебаний энергии) пройдет через поверхность  , тогда
, тогда
 .
.
Для монохроматической волны среднее по времени значение вектора 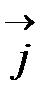 определяется выражением
определяется выражением
 ,
,
 – амплитуда волны,
– амплитуда волны,  – плотность среды,
– плотность среды, 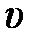 – фазовая скорость.
– фазовая скорость.
Скорость u света в среде

где с – скорость света в вакууме; n – абсолютный показатель преломления среды.
2. Оптическая длина пути световой волны

где  – геометрическая длина пути световой волны в среде с показателем преломления n.
– геометрическая длина пути световой волны в среде с показателем преломления n.
3. Оптическая разность хода двух световых волн

4. Зависимость разности фаз от оптической разности хода световых волн

где  – длина световой волны в вакууме.
– длина световой волны в вакууме.
5. Условие максимального усиления света при интерференции

6. Условие максимального ослабления света при интерференции
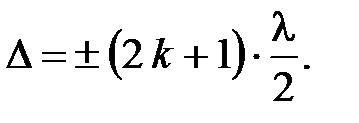
7. Оптическая разность хода световых волн, возникающих при отражении монохроматического света от тонкой плёнки, находящейся в вакууме или воздухе:
 или
или 
где d – толщина плёнки; n – показатель преломления;  – угол падения;
– угол падения;
 – угол преломления света в плёнке.
– угол преломления света в плёнке.
В оптическую разность хода добавляют поправку  , так как при отражении световой волны от оптически более плотной среды фаза колебаний вектора напряжённости электрического поля
, так как при отражении световой волны от оптически более плотной среды фаза колебаний вектора напряжённости электрического поля  в волне (светового вектора) меняется на p.
в волне (светового вектора) меняется на p.
8. Радиусы светлых колец Ньютона в отражённом свете (или тёмных в проходящем свете)
|
|
|

где k – номер кольца; R – радиус кривизны линзы; n – абсолютный показатель преломления среды в зазоре между линзой и пластинкой.
9. Радиусы тёмных колец Ньютона в отражённом свете (или светлых в проходящем свете)

10. Условие дифракционных максимумов от одной щели

где a – ширина щели;  – угол дифракции; k – порядковый номер максимума.
– угол дифракции; k – порядковый номер максимума.
11. Условие дифракционных минимумов от одной щели
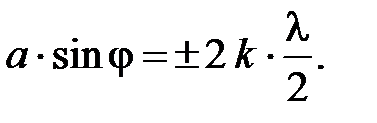
12. Условие главных максимумов на дифракционной решётке

где d – период дифракционной решётки;  – угол между нормалью к поверхности решётки и направлением на данный максимум;
– угол между нормалью к поверхности решётки и направлением на данный максимум;
k – порядковый номер главного максимума.
13. Закон Брюстера
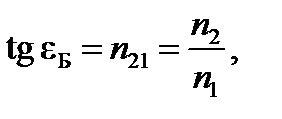
где 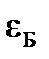 – угол Брюстера;
– угол Брюстера;  – относительный показатель преломления двух сред.
– относительный показатель преломления двух сред.
14. Закон Малюса

где 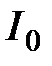 – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность плоскополяризованного света, вышедшего из анализатора;
– интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность плоскополяризованного света, вышедшего из анализатора;  – угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.
– угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.
15. Угол поворота  плоскости поляризации оптически активными веществами определяется по следующим формулам:
плоскости поляризации оптически активными веществами определяется по следующим формулам:
а) в твёрдых телах

где 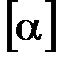 – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
– постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
б) в растворах

где С – массовая концентрация оптически активного вещества в растворе.
15. Степень поляризации
 ,
,
где Imax, Imin – соответственно, максимальная и минимальная интенсивности частично поляризованного света, прошедшего через систему поляризатора и анализатора.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 18. Определить длину звуковой волны ноты "Ля", если ей соответствующая частота колебаний равна 440 Гц, а скорость звука в воздухе 340 м/с?
Дано: n= 440 Гц, u = 340 м/с.
Решение. Записываем формулу, связывающую длину и скорость распространения волны
l = u/n,
Подставляем данные, вычисляем.
l = 340/440 = 0,78 м,
Ответ: 0,78 метра.
Пример 19. Волна распространяется со скоростью 10 м/с вдоль оси ОХ. Две точки, находящиеся на этой оси на расстоянии 6 м и 7,5 м от источника, колеблются по закону синуса с одинаковыми амплитудами А = 0,2 м и с разностью фаз ∆j = 0,75π. Найти длину волны λ; найти смещение указан- ных точек в момент времени t = 0,6 с.
Дано: u=10 м/с, х 1 = 6 м, х 2 = 7,5 м, А = 0,2 м, ∆j = 0,75π
Решение. Точки, находящиеся друг от друга на расстоянии, равном длине волны λ, колеблются с разностью фаз, 2π радиан; точки, находящиеся друг от друга на любом расстоянии ∆ х, колеблются с разностью фаз

Выразим и рассчитаем из этого уравнения длину волны λ

 .
.
Рассчитаем циклическую частоту колебаний
ω=2pn = 2pu/l ω=2p10/4= 5p, с-1.
|
|
|
Для расчета смещений указанных точек в момент времени t запишем уравнение плоской волны
x = A sin(ω t – kx),
где k =2π/λ – волновое число, или
x = A sin ω(t – x /u).
3. Найдем смещение x, подставляя в это уравнение значения t и х:
x1 = 0,1sin5π(0,6 – 6/10) = 0,1sin3π = 0;
x2 = 0,1sin5π(0,6 – 7,5/10) = -0,1 sin 0,75π = 1sin0,25π = -0,071 м.
Пример 20. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид
 .
.
Определить скорость распространения волны (фазовую скорость).
Дано:  .
.
Найти: u.
Решение. Уравнение плоской волны в среде без поглощения имеет вид
 ,
,
Сравнивая его с уравнением волны в условии задачи:
 ,
,
Получаем  ,
,  ,
,  ,
,
тогда  .
.
Ответ: u = 500 м/c.
| R |
| r |

 выпуклой стороной прижата к стеклянной пластинке (рис. 53). Расстояние между первыми двумя тёмными кольцами Ньютона, наблюдаемыми в отражённом свете, равно 0,5 мм. Определить радиус кривизны линзы, если освещение производится монохроматическим светом с длиной волны
выпуклой стороной прижата к стеклянной пластинке (рис. 53). Расстояние между первыми двумя тёмными кольцами Ньютона, наблюдаемыми в отражённом свете, равно 0,5 мм. Определить радиус кривизны линзы, если освещение производится монохроматическим светом с длиной волны 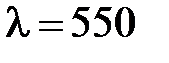 нм, падающим нормально.
нм, падающим нормально.
Рис. 53
Дано: n= 1,6;  мм =
мм =  м;
м;  нм =
нм =  м.
м.
Найти: R.
Решение. Для определения радиуса кривизны линзы R воспользуемся выражением для радиуса тёмных колец Ньютона в отражённом свете

Учитывая, что показатель преломления воздуха n = 1, получим
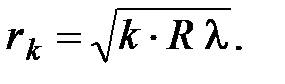
Разность радиусов первых двух тёмных колец
 (1)
(1)
Возведём левую и правую часть равенства (1) в квадрат
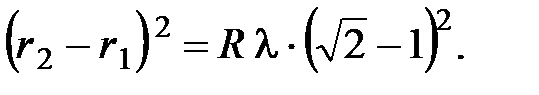 (2)
(2)
Выразим из соотношения (2) R

Выполним вычисления:
 м.
м.
Ответ: R = 2,65 м.
Пример 21. На дифракционную решётку длиной  мм, содержащей N = 300 штрихов, падает нормально монохроматический свет с длиной волны
мм, содержащей N = 300 штрихов, падает нормально монохроматический свет с длиной волны  нм. Определить: 1) число максимумов, наблюдаемых в спектре дифракционной решётки;2) угол, соответствующий последнему максимуму.
нм. Определить: 1) число максимумов, наблюдаемых в спектре дифракционной решётки;2) угол, соответствующий последнему максимуму.
Дано: 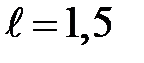 мм =
мм = 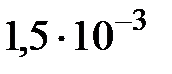 м; N = 300;
м; N = 300;  нм =
нм =  м.
м.
Найти: N; 
Решение. На рис. 53 изображён график зависимости интенсивности света на экране от расстояния x (I = f (x)).
| экран |
| решётка линза |
| I |
| j |
| X |
Рис.54
Период дифракционной решётки определим по формуле

Подставляя числовые данные, получим
 м =5 мкм.
м =5 мкм.
Условие главных максимумов для дифракционной решётки
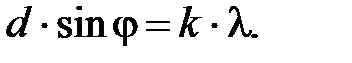 (1)
(1)
Поскольку наибольший угол отклонения лучей решёткой не может быть более 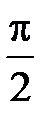 , из условия (1) можно найти максимальное значение
, из условия (1) можно найти максимальное значение  при
при  :
:

Подставляя данные, получим
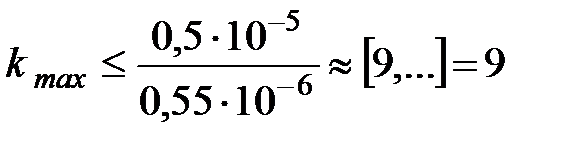 .
.
Число k должно быть обязательно целым. В то же время оно не может быть равным 10, так как при этом значении  будет больше единицы, что невозможно.
будет больше единицы, что невозможно.
Общее число максимумов, даваемых дифракционной решёткой:

Максимумы наблюдаются как справа, так и слева от центрального максимума, а единица учитывает центральный нулевой максимум.
Вычисляя, получим

Угол дифракции, соответствующий последнему максимуму, найдём, записав условие (1) в виде

Откуда

Выполним вычисления:

Ответ: N = 19; 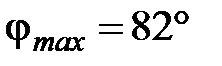 .
.
Пример 22. Определить, во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями  , и в каждом из николей теряется 8% интенсивности падающего света.
, и в каждом из николей теряется 8% интенсивности падающего света.
Дано:  ; k= 0,08.
; k= 0,08.
Найти: 
Решение. Согласно условию задачи изобразим рисунок (рис. 54)
| · · |
| · · |
| · · |
| N 1 |
| N 2 |
| П |
| А |
| I 0 |
| I |
| I ест |
| o |
| o |
| e |
| e |
| А |
| В |
Рис. 55
Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного лучепреломления на два пучка: обыкновенный (о) и необыкновенный (е). Оба пучка одинаковы по интенсивности и полностью поляризованы во взаимно перпендикулярных плоскостях. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа (). Плоскость колебаний обыкновенного пучка перпендикулярна плоскости чертежа (·). Обыкновенный пучок света (о) вследствие полного отражения от границы АB отбрасывается на зачернённую поверхность призмы и поглощается ею. Необыкновенный пучок (е) проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, прошедшего через первую призму:
 (1)
(1)
Плоскополяризованный пучок света c интенсивностью 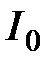 падает на второй николь
падает на второй николь  и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью поглощается призмой, поэтому интенсивностью его пренебрегаем. Интенсивность
и также расщепляется на два пучка различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью поглощается призмой, поэтому интенсивностью его пренебрегаем. Интенсивность  необыкновенного пучка лучей, вышедшего из призмы
необыкновенного пучка лучей, вышедшего из призмы  , определяется законом Малюса (без учёта поглощения света во втором николе):
, определяется законом Малюса (без учёта поглощения света во втором николе):

где  – угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя
– угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания николя  .
.
Учитывая потери интенсивности на поглощение во втором николе, получаем
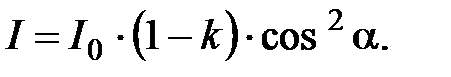 (2)
(2)
Заменяя в формуле (2)  выражением (1), получаем
выражением (1), получаем
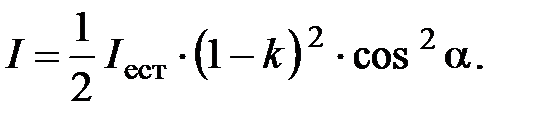
Тогда

Выполним вычисления

Ответ: 
3.5 Задачи к контрольной работе № 4
|
|
|


