Задачи к контрольной работе № 5 Элементы квантовой физики. Атом. Ядро.

Таблица 5

Вариант	Номера задач

 

1. Определить, во сколько раз уменьшится термодинамическая температура абсолютно черного тела при ослаблении ее энергетической светимости R _е в 16 раз.

2. Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости абсолютно черного тела, если его энергетическая светимость R _е=10⁴ Вт/м².

3. При охлаждении абсолютно черного тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, увеличилась на Δλ=8 мкм. Определить конечную температуру Т ₂, если начальная температура Т ₁=3000 К.

4. Максимум излучательной способности Солнца приходится на длину волны 500 нм. Определить мощность излучения и температуру ее поверхности. Солнца рассматривать как абсолютно черное тело. Принять радиус Солнца равным 695·10⁶ м.

5. Определить, на какую длину волны сместится максимум излучаемой абсолютно черным телом энергии, изначально приходящийся на длину волны λ=10^-5 м, если температура тела уменьшится на Δ Т =90 К.

6. Вычислить длину волны соответствующей максимальной спектральной плотности энергетической светимости (r _{λ ,T})_max абсолютно черного тела, равной 13·10¹⁰ (Вт/м²)/м.

7. Определить температуру Т внутри плавильной печи, если поток энергии Ф_е, излучаемый из ее смотрового отверстия (S =5 см²), равен 0,035 кВт.

8. Вычислить энергетическую светимость R _е и энергию W, излучаемую с поверхности угля площадью S = 5 см² за время t = 10 мин при температуре T =1000 К. Коэффициент теплового излучения а _тугля равен 0,85.

9. Температура Т внутри муфельной печи 1400 К. Печь потребляет мощность Р= 1,0 кВт. Определить, какая часть мощности рассеивается стенками, считая, что отверстие печи (S =20 см²) излучает как абсолютно черное тело.

10. Во сколько раз изменятся энергетическая светимость R _e и максимальная спектральная плотность энергетической светимости абсолютно черного тела при смещении максимума спектральной плотности (r _{λ ,T})_max с λ₁=2,7 мкм на λ₂=0,9 мкм?

11. При увеличении температуры абсолютно черного тела Т в два раза длина волны λ_m, на которую приходится максимум спектральной плотности энергетической светимости (r _{λ ,T})_max, уменьшилась на ∆λ =600 нм. Определить начальную и конечную температуры T ₁ и T ₂ абсолютно черного тела.

12. Вычислить для абсолютно черного тела относительное увеличение ∆ R _e /R _e энергетической светимости при увеличении его температуры на 2%.

13. При некоторой постоянной температуре Т мощность Р излучения шара радиусом R = 20 см равна 2 кВт. Вычислить эту температуру, считая шар серым телом с коэффициентом теплового излучения а _т = 0,30.

14. Вычислите длину волны λ_m, на которую приходится максимум спектральной плотности энергетической светимости (r _{λ ,T})_max черного тела при температуре Т = 273 К?

15. Определить поток энергии Ф _е, излучаемый с поверхности Сириуса, площадью S = 2 км², если температура Т ее верхних слоев равна 10⁴ К.

16. На поверхность серебра направили ультрафиолетовое излучение с длиной волны λ = 0,300 мкм. Будет ли при этих условиях наблюдаться фотоэффект?

17. Определить максимальную скорость u _max фотоэлектронов при облучении цинковой пластинки монохроматический светом с длиной волны λ=0,22 мкм.

18. Из металла (А _вых = 4,6 эВ) фотоны с энергией Е = 5 эВ выбивают фотоэлектроны. Вычислить максимальный импульс, передаваемый его поверхности при вылете электрона.

19. При облучении поверхности фотоэлемента светом с длиной волны λ=0,31 мкм фототок прекращается при некотором задерживающем напряжении. Если увеличить длину падающей волны на 25 %, то задерживающее напряжение уменьшится на 0,8 В. Вычислить постоянную Планка по этим данным.

20. Определить длину волны монохроматического света, падающего на поверхность алюминия, если фототок прекращается при задерживающем напряжении U ₃ =1 В. Для алюминия, красная граница фотоэффекта λ₀ = 332 нм.

21. Определить длину волны монохроматического света, освещавшего цинковый электрод, если работа выхода для цинка равна 4,0 эВ, а максимальная кинетическая энергия фотоэлектронов достигает 0,26 эВ.

22. Задерживающее напряжение для платиновой пластинки (А _вых=6,3эВ) равно 3,7 В. При тех же условиях, для другой пластинки, задерживающее напряжение составляет 5,3 В. Определить работу выхода электронов из неизвестной пластинки.

23. Свет, с частотой ν = 7,2·10¹⁴ Гц, падает на металлическую пластину. Определить максимальную скорость u _max фотоэлектронов, если красная граница фотоэффекта λ₀ для данного материала равна 0,560 мкм.

24. Свет с длиной волны λ = 150 нм падает на поверхность рубидия (А _вых=2,1 эВ). Определить максимальную кинетическую энергию Т _mах фотоэлектронов. Ответ выразите в эВ.

25. При облучении монохроматическим светом поверхности металла, для которого красная граница фотоэффекта λ₀= 306 нм максимальная кинетическая энергия Т _mах вырываемых электронов равна 1,2 эВ. Вычислить долю энергии фотона, израсходованную на работу вырывания фотоэлектрона в этом случае.

26. Поверхность калия (А _вых=2,2 эВ) освещается монохроматическим светом с длиной волны 350 нм. Вычислить наименьшее значение задерживающего напряжения, при котором прекратится фототок.

27. Определить постоянную Планка по данным опыта, когда электроны, вырываемые из металла светом с частотой ν ₁ = 4,6·10¹⁵ Гц полностью задерживаются напряжением U ₁ = 16,5 В, а вырываемые светом с частотой ν ₂ = 2,2·10¹⁵ Гц - напряжением U ₂ = 6,6 В.

28. Вычислить длину волны λ падающего на поверхность платиновой пластинки (А _вых=5,32 эВ) излучения, если вырванные из нее фотоэлектроны полностью задерживаются полем с разностью потенциалов U = 0,7 В.

29. Для некоторого металла красная граница фотоэффекта соответствует частоте излучения ν ₀=0,6·10¹⁵ Гц. Определить частоту падающего света ν, если вырывающиеся из металла электроны задерживаются полем с разностью потенциалов U = 3 эВ.

30. Фотоны с энергией E = 5,3 эВ выбивают фотоэлектроны из металла (А _вых = 4,7 эВ). Вычислить максимальный импульс фотоэлектрона и напряжение его задержки.

31. Вычислить массу т, импульс р и энергию Е фотона, длина волны которого λ=0,380 мкм.

32. С какой скоростью электрон должен двигаться, чтобы его импульс был равен импульсу фотона, длина волны которого λ=2,1 пм?

33. При какой температуре средняя энергия молекул трехатомного газа равна энергии фотонов, соответствующих излучению с длиной волны λ = 630 нм?

34.Давление р, оказываемое светом на зеркальную поверхность при нормальном падении лучей, равно 10^-5 Па. Определить поверхностную плотность I потока падающей энергии.

35. Определить концентрацию п фотонов в монохроматическом световом пучке света (λ=660 нм) производящем на зачерненную поверхность давление р= 300 нПа. Свет падает на поверхность в направлении нормали к ней.

36. Поток энергии Ф _е, излучаемый электрической лампой, равен 600 Вт. Определить силу F светового давления на зеркало, расположенное на расстоянии r = 1 м от лампы перпендикулярно падающим лучам. Диаметр d =2,0 см. Считаем, что излучение лампы одинаково во всех направлениях.

37. Энергия фотона Е =10⁶ эВ. Вычислить его длину волны λ, массу т и импульс р.

38. Определить давление монохроматического света, оказываемое на зеркальную поверхность площадью S = 5 см², если известно, за 180 секунд на нее падает световая энергия W = 10 Дж. Свет падает на поверхность в направлении нормали к ней.

39. Определить число N фотонов в пучке монохроматического света (λ=500 нм), ежесекундно падающих на плоскую зеркальную поверхность, в направлении нормали к ней, если производимое на нее давление осуществляется с силой F =10 нН.

40. Давление р монохроматического света с длиной волны (λ=600 нм), создаваемое на зачерненую поверхность, расположенную перпендикулярно падающим лучам, равно 0,2 мкПа. Определить плотность потока фотонов (число фотонов, приходящихся на 1 м² облучаемой поверхности за 1 секунду, в направлении нормали к ней), в падающем пучке света.

41. На зеркало площадью S =1,4 см² с идеально отражающей поверхностью нормально падает монохроматический свет. Поверхностная плотность потока падающего излучения I, равна 0,12 МВт/м². Определить импульс р, полученный зеркалом, если длительность облучения t = 1с.

42. Определить давление света на стенки электрической 150-ваттной сферической лампочки (R =5 см), принимая, что вся потребляемая мощность идет на излучение и стенки лампочки отражают 20 % падающего на них света.

43. Вычислить длину волны λфотона, если его масса равна массе покоя: 1) протона; 2) электрона.

44. Давление р монохроматического света (λ=550 нм) на зачерненную поверхность (S = 50 см²), расположенную перпендикулярно падающему излучению, равно 0,155 мкПа. Определить число N фотонов, падающих на нее за время t =3 с.

45. Вычислить длину волны λ фотона, импульс которого равен импульсу электрона, движущегося со скоростью u = 0,1·10⁸ м/с.

46. При комптоновском рассеянии рентгеновского излучения под углом θ = 60⁰ длина волны рассеянного излучения оказалась равной 56 пм. Определить длину волны исходного излучения.

47. Фотон с энергией Е =1,03 МэВ рассеивается на свободных электронах на угол θ = 150⁰ (эффект Комптона). Вычислить энергию Е ′ рассеянного фотона.

48. Определить максимальное изменение длины волны фотонов при эффекте Комптона, если рассеяние происходит: 1) на свободных протонах; 2) на свободных электронах.

49. На изначально покоившемся свободном электроне рассеивается фотон с энергией Е =250 кэВ, при этом длина волны рассеянного фотона изменилась на 25%. Вычислить кинетическую энергию электрона отдачи.

50. Энергия Е падающего фотона до равна λ = 255 кэВ. Вычислить долю энергии фотона при эффекте Комптона, которая пришлась на электрон отдачи, если угол рассеяния составил θ=180°.

51. Энергия Е падающего фотона при комптоновском рассеянии распределяется поровну между электроном отдачи и рассеянным фотоном. Определить энергию Е ' и импульс р ' рассеянного фотона, если угол рассеяния составил θ = 90°

52. Вычислить угол рассеяния θ пучка фотонов на свободных электронах при эффекте Комптона, если исходный фотон, с энергией Е = 250 кэВ, а энергия Е ' рассеянного фотона 200 кэВ.

53. На свободных электронах рассеивается поток фотонов (эффект Комптона) с длиной волны λ=1 пм. Определить долю энергии исходных фотонов, переданную электронам, если угол рассеяния θ=90°.

54. Вычислить кинетическую энергию электрона отдачи (эффект Комптона), если известно, что фотон с энергией Е = 0,250 МэВ рассеялся под углом θ=120° на покоившемся свободном электроне.

55. Фотон с энергией, равной энергии покоя электрона (эффект Комптона) рассеивается под углом θ = 180°. Определить импульс р электрона отдачи

56. При эффекте Комптона на графите происходит рассеивание излучения с длиной волны λ = 55,7 пм под углом θ = 60° к исходному направлению падающего пучка света. Определить длину волны λ' рассеянного излучения.

57. На изначально покоившемся свободном электроне фотон с длиной волны λ =5,1 пм испытывает комптоновское рассеяние под углом θ=90°. Найти: 1) изменение длины волны при рассеянии; 2) энергию электрона отдачи.

58. При рассеянии фотона на свободном электроне изменение длины волны ∆λ в рассеянном потоке составило 3,60 пм. Определить угол θ рассеяния.

59. Определить кинетическую энергию электрона отдачи, если фотон с энергией Е = 0,1 МэВ в результате эффекта Комптона рассеялся на угол θ = 90°.

60. Вычислить долю w₁ энергии фотона при эффекте Комптона, приходящуюся на рассеянный фотон, и долю w₂ этой энергии, полученную электроном отдачи. Угол рассеяния θ = 65°. Энергия Е падающего фотона равна энергии покоя электрона.

61. Вычислить максимальную длину волны линии серии Бальмера, если максимальная длина волны спектральной линии серии Лаймана атома водорода равна 120 нм. Считать постоянную Ридберга неизвестной.

62. При переходе электрона в атоме водорода с шестой боровской орбиты на вторую испускается фотон. Вычислить длину волны фотона, испущенного атомом при этом переходе. Определить серию спектра, к которой относится эта линии.

63. При переходе электрона с третьего энергетического уровня на первый атом водорода испускает фотон. Определить энергию этого фотона?

64. Определить наименьшую Е _min и наибольшую Е _max энергии фотона для ультрафиолетовой серии (серии Лаймана) спектра атома водорода.

65. Определить длины волн для границ серий Лаймана, Бальмера и Пашена.

66. Из невозбужденного атома водорода фотон, с энергией Е =16,0 эВ, выбивает электрон. Определить скорость u электрона вдали от ядра атома.

67. Определить частоту ν вращения электрона на третьей стационарной орбите иона гелия.

68. Рассчитать потенциал U_i и энергию ионизации E_i для однократно ионизированного атома гелия He ⁺ и двукратно ионизированного атома лития Li ⁺⁺.

69. Определить длины волн трех спектральных линий, испускаемых атомарным водородом при переходе возбужденного состояния в основное. Указать, каким сериям принадлежат эти линии.

70. Определить частоту фотона, излучаемого атомом водорода при переходе электрона на уровень с главным квантовым числом n =2, если радиус его орбиты изменился в 9 раз.

71. По третьей орбите атома водорода вращается электрон. Определить его скорость u и частоту вращения n.

72. Находящийся в основном состоянии атом водорода поглотил квант света с длиной волны λ = 121,5·10^-9 м. Вычислить радиус r орбиты, на которую перейдет электрон при возбуждении атома водорода.

73. Для однократно ионизированного атома гелия Не ⁺ вычислить длину волны λ, испускаемую им, при переходе электрона со второго энергетического уровня на первый. Выполнить такой же подсчет для двукратно ионизированного атома лития Li ⁺⁺.

74. Для электрона, находящегося на второй стационарной орбите в атоме водорода, вычислить кинетическую Т, потенциальную П и полную Е энергии.

75. В атоме водорода, при излучении атомом фотона с длиной волны λ = 0,486 мкм изменилась кинетическая энергия электрона. Определить, как и на сколько она изменилась.

76. Кинетическая энергия электрона равна 10⁶ эВ. Определить длину волны λ де Бройля.

77. Длина λ волны де Бройля для протона равна 10^-9 м. Определить ускоряющую разность потенциалов, которую прошел протон.

78. Заряженная частица, прошедшая ускоряющую разность потенциалов U = 500 В, имеет длину волны де Бройля λ = 1282 фм. Определить массу этой частицы, если ее заряд равен заряду электрона.

79. Определить длину λ волны де Бройля для протона, движущегося в однородном магнитном поле с индукцией B =0,015 Тл по окружности радиусом R =140 см.

80. Определить длину λ волны де Бройля электрона, который движется со скоростью u = 20·10⁷ м/с. При решении задачи учесть изменение массы электрона в зависимости от скорости.

81. Длина λ волны де Бройля электрона равна его комптоновской длине волны λ_К. С какой скоростью движется электрон?

82. Электрон находится на второй орбите атома водорода. Найти длину λ волны де Бройля электрона.

83. Протон прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля λ протона, если: 1) U = 1000 В; 2) U = 10⁶ В.

84. Электрон движется в атоме водорода со скоростью u =1,5·Мм/с. Определить неопределенность Δ x в определении его координаты, если в определении скорости допускается неопределенность Δ u = 0,1u.

85. В металлической крошке диаметром d = 10^-6 м находится электрон с кинетической энергией Т = 0,015 кэВ. Оценить относительную неопределенность Δ u / u, с которой может быть определена скорость электрона.

86. В соответствии с принципом неопределенностей Гейзенберга, показать, почему в ядре не могут находиться электроны. Принять линейные размеры ядра равными 5 фм.

87. Определить относительную неопределенность Δ р / р импульса частицы, если неопределенность координаты равна ее длине волны де-Бройля.

88. Вычислить отношение неопределенности Δ x координаты частицы к ее длине волны де-Бройля, если относительная неопределенность импульса частицы Δ р / р =0,01.

89. На фотопластинке ширина следа электрона, имеющего кинетическую энергию Т = 1500 эВ, полученного с помощью камеры Вильсона, составляет Δ x = 10^-6 м. Определить, возможно ли обнаружение отклонения в движении электрона по данному следу от законов классической механики.

90. Пучок электронов ускоряется разностью потенциалов U = 10³ В. Известно, что неопределенность их скорости составляет 0,1% от ее величины. Рассчитать неопределенность координаты отдельного электрона в пучке. Будет ли электрон классической или квантовой частицей в данных условиях?

91. Определить вероятность обнаружения частицы в первой трети одномерного прямоугольного «потенциального ящика» шириной l c бесконечно высокими «стенками», если частица находится в основном состоянии.

92. В одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» шириной l находится частица в возбужденном состоянии (n = 2). Вычислить вероятность нахождения частицы в области 3/8 l ≤ x ≤ 5/8 l.

93. В одномерной прямоугольной «потенциальной яме» c бесконечно высокими «стенками» шириной l находится частица в возбужденном состоянии (n = 3). Определить, в каких ее точках (0≤ x ≤ l) плотность вероятности максимальна. Решение задачи пояснить графически.

94. В одномерной прямоугольной «потенциальной яме» c бесконечно высокими «стенками» шириной l находится частица в возбужденном состоянии (n = 3). Определить, в каких ее точках (0≤ x ≤ l) плотность вероятности минимальна. Решение задачи пояснить графически.

95. Определить, в каких точках потенциальной ямы шириной l плотность вероятности нахождения электрона на первом и втором энергетических уровнях одинакова? Вычислить плотность вероятности в этих точках. Ответ пояснить графически.

96. Определить вероятность W нахождения частицы во второй трети одномерной прямоугольной «потенциальной яме», если частица находится в основном состоянии?

97. Определите отношение разности соседних энергетических уровней Δ Е_{n +1, n} к энергии Е_n частицы, находящейся одномерной прямоугольной «потенциальной яме», для состояний: 1) n =4; 2) n =8; 3) n =∞.

98. В одномерной прямоугольной «потенциальной яме» шириной l = 5·10^-10 м. находится электрон. Вычислить наименьшую разность Δ Е энергетических уровней электрона. Ответ выразите в электронвольтах.

99. Определить вероятность обнаружения частицы в интервале 1/4 равноудаленном от стенок одномерной прямоугольной «потенциальной ямы», если она находится в низшем возбужденном состоянии.

100. Определить отношение вероятностей W ₁/ W ₂ нахождения электрона на первом и втором энергетических уровнях в интервале l /4 равноудаленном от стенок одномерной потенциальной ямы (l – ее ширина).

101. Определить среднее значение координаты ‹ x › электрона, находящегося в одномерной прямоугольной «потенциальной яме» шириной l (0< x < l).

102. Определить вероятность обнаружения частицы в первой трети одномерной прямоугольной «потенциальной ямы» шириной l c бесконечно высокими «стенками», если частица находится в основном состоянии.

103. Определить, в каких точках одномерной прямоугольной «потен-циальной ямы» шириной l c бесконечно высокими «стенками» (0≤ x ≤ l) плотность вероятности минимальна, если частица находится в возбужденном состоянии (n = 2).

104. Определить, в каких точках одномерной прямоугольной «потенциальной ямы» шириной l c бесконечно высокими «стенками» (0≤ x ≤ l) плотность вероятности максимальна, если частица находится в возбужденном состоянии (n = 2). Пояснить ответ графически.

105. Определить вероятность обнаружения частицы в области l/2 ≤ x ≤ l одномерной прямоугольной «потенциальной ямы» шириной l c бесконечно высокими «стенками», если частица находится в возбужденном состоянии (n = 2).

106. Период полураспада радиоактивного изотопа тория (Т _1/2=7000 лет). Определить, какая часть начального количества атомов распадется за 100 лет.

107. Во сколько раз уменьшится начальное количество радиоактивного изотопа за два года, если за один год начальное количество радиоактивного изотопа уменьшилось в три раза?

108. Период полураспада радиоактивного изотопа T _1/2 = 1 сутки. За какое время t распадется 1/4 начального количества ядер этого вещества?

109. Определить среднюю продолжительность τ жизни радиоактивного нуклида, если период полураспада T _1/2 этого нуклида равен 60 мин.

110. Определить через какое количество периодов полураспада T _1/2 активность А радиоактивного препарата уменьшится в k = 250 раз.

111. Период полураспада T _1/2 радиоактивного изотопа иридия 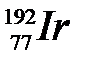равен 75 суток. Определить, на сколько процентов снизится активность А изотопа за время t = 30 суток?

112. Для фосфора массой m = 1 мг определите активность А.

113. Какова удельная активность а кобальта ?

114. Определить период полураспада T _1/2 радиоактивного изотопа, если за время t = 8 суток распалось k =3/4 начального количества его ядер.

115. Стронций массой m ₂ = 1 мг имеет такую же активность А, как уран . Найти массу m ₁ урана.

116. За время t = 849с распалось 5/8 исходного количества ядер радиоактивного изотопа. Определить период его полураспада.

117. Вычислить количество ядер радиоактивного изотопа, которое распадется за время t, равное двум периодам полураспада T _1/2.

118. Вычислить активность некоторого радиоактивного изотопа по истечении промежутка времени, равного половине периода полураспада, если в начальный момент времени активность изотопа составляла 100 Бк.

119. Период полураспада изотопа урана T _1/2 = 4,5·10⁹ лет. Определить удельную активность а этого изотопа (активность, приходящаяся на единицу массы радиоактивного вещества).

120. Определить, какая доля начального количества радиоактивного изотопа останется нераспавшейся через три года, если за один год его начальное количество уменьшилось в четыре раза?

121. Для ядра атома тяжелого водорода вычислить дефект массы Δ m и энергию связи Е _св.

122. Вычислить энергию Е _св, освободившуюся при соединении одного протона и двух нейтронов в атомное ядро.

123. Определить массу m _а нейтрального атома, ядро которого состоит из двух протонов и одного нейтрона. Энергия связи Е _св = 7,72 МэВ.

124. Определить энергию Е, которую нужно затратить для разделения его на отдельные нуклоны ядер и ?

125. Определите наименьшую энергию Е, которую нужно затратить, чтобы оторвать один нейтрон от ядра азота .

126. Рассчитать минимальную энергию Е, которую необходимо затратить для удаления одного протона из ядра азота ?

127. Определите наименьшую энергию Е необходимую для разделения ядра на две одинаковые части.

128. Определите наименьшую энергию Е необходимую для разделения ядра на три одинаковые части?

129. Найти удельную энергию связи Е _уд ядра углерода .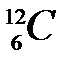

130. Определить массу m _а нейтрального атома ядра, состоящего из трех протонов и четырех нейтронов, если его энергия связи Е _св равна 39,3 МэВ.

131. Вычислить энергию, соответствующую дефекту массы Δ m = 3 мг. Ответ записать в электронвольтах.

132. Энергия связи Е _св ядра, состоящего из трех протонов и двух нейтронов, равна 26,3 МэВ. Определить массу m _а нейтрального атома.

133. Вычислить удельную энергию связи Е _уд ядра гелия .

134. Для ядра атома фтора вычислить дефект массы Δ m и энергию связи Е _св.

135. Определите наименьшую энергию Е необходимую для отрыва нейтрона от ядра натрия ?

136. Рассчитать энергию ядерных реакций:

1) ; 2) .

Определить, с поглощением или выделением энергии протекает реакция.

137. Дейтрон может расщепиться на два нуклона, при взаимодействии с γ-фотоном. Запишите уравнение ядерной реакции и вычислите минимальную энергию γ – фотона, вызывающего такое расщепление.

138. Энергия связи Е _св ядра равна 104,66 МэВ, а ядра 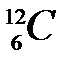– 105,29 МэВ. Определите энергию Q ядерной реакции (n,p) .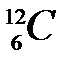

139. Вычислить энергию ядерных реакций:

1) ; 2) .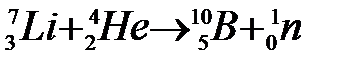

Определить, с поглощением или выделением энергии протекает реакция.

140. Определить кинетические энергии Т ₁ и Т ₂ и импульсы p ₁ и p ₂ продуктов реакции , если пренебречь кинетическими энергиями ядер дейтерия и принять их суммарный импульс равными нулю.

141.Вычислить энергию Q следующих ядерных реакций:

1) (p, g) ; 2) (p, a) .

142. Энергия связи Е _св ядра равна 58,16 МэВ, а ядра 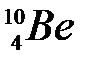– 64,98 МэВ. Найти энергию Q ядерной реакции (n, g) .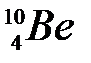

143. Определить массу m ,если в результате реакции (d,p) освобождается энергия Q = 5,028 МэВ. Масса нейтрального атома m = 7,01601 а.е.м., масса дейтона m_d = 2,01355 а.е.м., масса протона m_р = 1,00728 а.е.м.

144. Определить массу m атома , если при реакции (d,p) выделяется энергия Q = 4,033 МэВ. Масса нейтрального атома 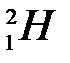m = 2,01410 а.е.м., масса дейтона m_d = 2,01355 а.е.м., масса протона m_р = 1,00728 а.е.м.

145. При захвате одного нейтрона ядро урана 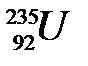делится на два осколка и два нейтрона. Один из осколков - ядро ксенона . Определить порядковый номер Z и массовое число А другого осколка.

146. При бомбардировке дейтонами изотопа лития образуются две α – частицы. Определить массу изотопа лития , если при этом выделилась энергия Q = 22,3 МэВ, а масса дейтона m_d = 2,01355 а.е.м. и масса α – частицы m _α = 4,00149 а.е.м.

147. Вычислить энергию, которая выделится при делении всех ядер, содержащихся в m = 10^-3 кг 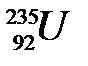, если реакция деления имеет вид .

148. Вычислить энергию ядерных реакций:

а) ; б) .

149. Какая энергия Q выделится в результате α – распада ядра полония .

150. В результате распада ядро углерода выбросило позитрон и нейтрино. Определить энергию Q, выделившуюся в результате этой реакции.

 

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: