Колебания. Волны. Волновая оптика.

Таблица 4

Вариант	Номера задач

 

1. Вычислить, за какое время, считая от начала движения, тело, совершающее гармонические колебания с периодом Т = 4с сместиться от положения равновесия на половину амплитуды. Начальную фазу колебаний считать равной нулю.

2. Вычислить для материальной точки, совершающей гармонические колебания и периодом Т =5с максимальную скорость u_max и максимальное ускорение а _max.

3. Материальная точка совершает свободные гармонические колебания с амплитудой А = 20 см. Вычислить циклическую частоту ω колебаний и максимальное ускорение а_max точки, если ее наибольшая скорость u _max =0,4 м/с.

4. Определить амплитуду А, циклическую частоту ω, период Т и фазу (ω t +φ₀) колебаний точки, колеблющейся по закону х = А cos(w t +j₀), если в некоторый момент времени смещение x точки равно 0,05 м, ее скорость u = 0,20 м/с и ускорение а = - 0,80 м/с².

5. Скорость точки в некоторый момент времени u=8 см/с. Определить модуль ее ускорения в этот момент времени, если известно, что точка совершает колебания по закону х = А cos w t, где А =5,0 см; ω=2 с^-1.

6. Составить уравнение гармонических колебаний точки с начальной фазой π/6, амплитудой 2 см и периодом 2 с. Для момента времени t = π с вычислить ее скорость и ускорение.

7. Материальная точка совершает гармонические колебания по закону х = А sin w t. В момент времени t ₁ смещение точки x ₁=30 см. В момент времени t ₂ фаза колебаний увеличилась в два раза и смещение x ₂ стало равным 48 см. Определить амплитуду А колебаний точки.

8. Записать зависимость смещения материальной точки от времени, если ее скорость, задается уравнением х = - 6sin p t.

9. Точка совершает колебания по закону х = 7sin 0,5p t. Определить промежуток времени, за который она пройдет путь от положения равновесия до максимального смещения.

10. Материальная точка совершает гармонические колебания. Амплитуда колебаний А равна 5,0 см, период колебаний Т = 2 с. Определить скорость точки в момент времени, когда смещение точки от положения равновесия равно 2,5 см. Начальная фаза колебаний равна нулю.

11. Определить амплитуду и период гармонического колебания, если при смещении точки от положения равновесия x ₁ =24 мм, скорость u ₁= 30 мм/с, а при смещении x ₂ = 28 мм, скорость u ₂= 20 мм/с. Начальная фаза колебания равна нулю.

12. Максимальное ускорение точки а_max = 50 см/с², период колебаний Т = 2с, смещение точки от положения равновесия в начальный момент времени x ₀ = 2,5 см. Написать уравнение ее гармонических колебаний.

13. Точка совершает колебания по закону х = 10sin 0,5p t. Определить промежуток времени, за который она пройдет путь от положения равновесия до половины максимального смещения.

14. Определить амплитуду колебаний материальной точки, совершающей гармонические колебания с частотой ν = 1 Гц, если известно, что в начальный момент времени координата точки x ₀ =5,0 см, скорость u₀ = 15 см/с.

15. Для материальной точки, совершающей гармонические колебания с амплитудой А = 3,5 см и периодом Т = 6 с определить максимальные значения скорости и ускорения.

 

16. Вычислить полную энергию Е_max материальной точки массой m = 40 г совершающей гармонические колебания по закону х =0,2cos(4p t +p/4), м.

17. Материальная точка совершает колебания по закону х = А cos(w t +j₀) где А =2,5 см и ω=π/6 с^-1. Когда возвращающая сила F в первый раз достигает значения -6 мН, потенциальная энергия Е _п равна 75 мкДж. Определить этот момент времени t и соответствующую ему фазу колебаний j = w t +j₀.

18. Максимальная сила F _max, действующая на колеблющуюся точку, равна – 10·10^-4 Н, а ее полная энергия Е равна 2·10^-5 Дж. Составить уравнение движения этой точки, если период Т колебаний равен p с, а начальная фаза φ=π/4.

19. Тело массой m = 40 г совершает гармонические колебания по закону х =0,2 cos1,5p t, м. Вычислить возвращающую силу F и полную энергию Е точки для момента времени t = 0,5 с.

20. Определить максимальные значения возвращающей силы F _max и кинетической энергии Т _max для материальной точки массой m = 20 г, если она колеблется по закону х =0,1cos(4p t +p/4), м.

21. Шарик совершает гармонические колебания с амплитудой А =15 см. Определить его смещение от положения равновесия за время, в течение которого его кинетическая энергия уменьшится вдвое.

22. Груз совершает вертикальные колебания на пружине с амплитудой А =6,0 см. Коэффициент жесткости пружины k =0,500 кН/м. Определить его потенциальную и кинетическую энергии в момент времени, смещение от положения равновесия составит половину амплитуды.

23. Точка совершает гармонические колебания. Определить отношение кинетической энергии к ее потенциальной энергии для моментов времени: t = Т/ 10 с; t = Т/ 3 с. Начальную фазу колебаний считать равной нулю.

24. Шарик массой m =65 г совершает колебания с частотой n = 0,5Гц. Смещение шарика в начальный момент времени равно 40 мм, а энергия Е равна 20 мДж. Написать уравнение его гармонических колебаний и зависимость возвращающей силы от времени.

25. Полная энергия Е гармонически колеблющейся точки равна 20 мкДж, а максимальная сила F _max, действующая на точку, равна – 0,4 мН. Написать ее уравнение движения, если период Т =5 с, а начальная фаза φ=π/4.

26. Амплитуда гармонических колебаний материальной точки А = 2,0 см, полная энергия колебаний Е =0,3 мкДж. Определить ее смещение от положения равновесия, если в этот момент времени на точку действует возвращающая сила 22,5 мкН.

27. Материальная точка массой m =5 г совершает гармонические колебания по закону х =0,02cos(2p t +p/3), м. Определить максимальные значения возвращающей силы F _max и кинетической энергии Т _max.

28. Материальная точка совершает гармонические колебания на с амплитудой 0,3 м. Найти ее смещение от положения равновесия за время, в течение которого кинетическая энергия уменьшается в три раза.

29. Определить отношение потенциальной энергии точки, совершающей гармонические колебания, к ее кинетической энергии для момента времени, когда смещение точки от положения равновесия составит: x ₁ = А /4; x ₂ = А /2, где А – амплитуда колебаний.

30. Свободные пружины пренебрежимо малой массой при подвешивании к ним грузов массами m ₁ = 0,6 кг и m ₂ = 0,4 кг, соответственно, одинаково удлинились на 0,1 м. Определить, как и во сколько раз отличаются энергии пружин, если амплитуды колебаний грузов равны.

31. Два одинаковых грузика закреплены на концах тонкого невесомого стержня длиной l =0,30 м. Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на d =0,10 м от одного из концов стержня. Определить приведенную длину L и период Т колебаний такого физического маятника.

m

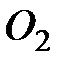
Рис. 56

Рис. 57

 

32. Определить, на каком расстоянии от центра масс должна быть точка подвеса тонкого однородного стержня длиной 60 см, чтобы частота его колебаний была максимальной.

33. В тонком однородном диске радиусом R =0,40 м вырезана часть, имеющая вид круга радиусом r = 0,20 м, так, как это показано на рис. 55. Оставшаяся часть диска колеблется относительно горизонтальной оси О, проходящей через образующую цилиндрической поверхности диска. Найти период Т колебаний такого маятника.

34. Система из трех грузов, представляющих из себя материальные точки, соединены стержнями длиной l =50 см (рис.56), колеблется относительно горизонтальной оси, проходящей через точку О перпенди-кулярно плоскости чертежа. Найти период Т колебаний системы. Массами стержней пренебречь.

35. Физический маятник в виде тонкого прямого стержня длиной l ₂=90 см и математический маятник длиной l ₁=60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние а от центра масс стержня до оси колебаний.

36. На гвоздь, вбитый горизонтально в стену, повешен тонкий обруч, который колеблется в плоскости, параллельной стене. Радиус R обруча равен 50 см. Вычислить частоту ν колебаний обруча.

37. Набухшее бревно с одинаковым сечением по всей длине, погружено вертикально в воду так, что над водой находится лишь малая его часть. Период T колебаний бревна равно 6 c. Вычислить длину l бревна.

38. Вычислить приведенную длину L и период T колебаний диска радиусом R =25 см колеблющегося около горизонтальной оси, проходящей через точку, удаленную на R/4 от его образующей, перпендикулярно его плоскости.

Рис. 58

39. Физический маятник, представляющий собой тонкий однородный стержень массой m и длиной 2 м с укрепленными на нем двумя маленькими шариками массами m и 2 m (рис. 57), совершает колебания около горизонтальной оси, проходящей через точку О на стержне. Вычислить частоту ν гармонических колебаний маятника. Шарики считать материальными точками.

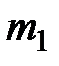
40. Грузик подвесили к спиральной пружине, в результате чего пружина растянулась на x = 90 мм. Определить период колебаний грузика, если грузик немного оттянуть вниз и затем отпустить.

 

Рис. 59

41. На концах тонкого стержня длиной l = 0,50 м укреплены по одинаковому грузику. Система колеблется под действием силы тяжести в вертикальной плоскости вокруг горизонтальной оси, которая делит длину стержня в отношении η = 4/5. Определить период колебаний маятника, если массой стержня пренебречь.

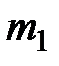
42. Определить период Т колебаний математического маятника длиной l = 40 см, подвешенного в кабине самолета, если самолет движется: 1) равномерно; 2) горизонтально с ускорением а = 2,0 м/с².

Рис. 60

43. Между двумя пружинами с коэффициентами жесткости k ₁=42 Н/м и k ₂ = 35 Н/м помещено тело массой m =1,5 кг (рис. 58). Определить период свободных колебаний такого маятника.

44. Физический маятник представляет собой систему, состоящую из тонкого однородного стержня массой m и длиной l = 1 м, с укрепленными на нем двумя маленькими шариками массами m и 2 m (рис. 59). Система совершает колебания около горизонтальной оси, проходящей через точку О на стержне. Определить период Т гармонических колебаний маятника. Шарики принять за материальные точки.

45. Шар радиусом R = 5,0 см подвешен на нити длиной l = 25 см. Вычислить период Т колебаний такого маятника.

46. За время t ₁= 5 мин амплитуда затухающих колебаний маятника уменьшилась в два раза. Определить время t ₂, считая от начального момента, в течение которого амплитуда уменьшится в восемь раз.

47. Определить логарифмический декремент затухания Λ, если за 10 минут амплитуда колебаний маятника длиной l = 1,0 м уменьшилась в два раза.

48. К спиральной пружине жесткостью k = 20 Н/м подвешена гиря массой m = 0,5 кг, которая совершает колебания в упругой среде. Логарифмический декремент затухания Λ = 4·10^-3. Определить число N полных колебаний и время t, за которое амплитуда колебаний маятника уменьшается в 2 раза.

49. За 60 секунд тело массой m = 6 г, совершающее затухающие колебания, потеряло 60 % своей энергии. Определить коэффициент сопротивления r.

50. Логарифмический декремент затухания маятника имеет значение Λ=62,8·10^-2. Вычислить частоту затухающих колебаний, если период T ₀ собственных колебаний системы равен 1 с.

51. Определить время t, за которое энергия колебаний математического маятника длиной l = 0,25 м, совершающего затухающие колебания, уменьшится в 9,5 раза, если логарифмический декремент затухания 0,015?

52. Маятник длиной l = 50 см совершает небольшие колебания в среде, коэффициент затуханий которой δ = 0,9 с^-1. Определить время τ и число полных колебаний N, за которые амплитуда колебаний маятника уменьшится в 4 раза.

53. Во сколько раз уменьшится амплитуда колебаний математического маятника за четыре полных колебания, если логарифмический декремент затухания Λ равен 0,3?

54. Определить время, за которое амплитуда математического маятника длиной 0,5 м уменьшится в е раз (е – основание натурального логарифма), если первое максимальное отклонение от положения равновесия А ₁ равно 50 мм, а второе А ₂ = 40 мм.

55. Определить, во сколько раз изменится ускорение точки в ее крайнем положении за одно полное колебание, если точка совершает затухающие колебания с логарифмическим декрементом затухания Λ, равным 0,25.

56. Определить коэффициент сопротивления r упругой среды, если тело массой m = 0,1 кг совершающее в ней затухающие колебания за60 с, потеряло 40 % своей энергии.

57. За два последовательных колебания системы с периодом затухающих колебаний T = 0,5 с амплитуда уменьшилась в 1,66 раза. Вычислить частоту собственных колебаний ν₀ системы и коэффициент затухания δ.

58. Система совершает 100 колебаний за 100 с, при этом амплитуда колебаний уменьшилась в 2,7 раза. Определить: 1) коэффициент затухания δ; 2) логарифмический декремент затухания Λ.

59. Определить время t ₂, за которое амплитуда затухающих колебаний уменьшилась в 100 раз, если за время t ₁= 10 с амплитуда уменьшилась в 10 раз.

60. Определить число полных колебаний маятника за промежуток времени, в течение которого амплитуда колебаний уменьшилась в три раза. Логарифмический декремент затухания Λ равен 0,012.

61. Определить частоту ν₀ собственных колебаний колебательной системы, если частота затухающих колебаний ν_зат = 1 кГц, а резонансная частота ν_рез = 0,998 кГц.

62. В упругой среде с коэффициентом сопротивления r = 20·10^-3 кг/с пружинный маятник жесткостью k =10 Н/м совершает вынужденные колебания. Определить коэффициент затухания δ и резонансную амплитуду А _рез, если амплитудное значение вынуждающей силы F ₀ = 10^-2 Н.

63. Определить резонансную частоту ν_рез, если амплитуды установившихся вынужденных колебаний при частотах ν₁ = 0,4 кГц и ν₂ = 0,6 кГц равны между собой. Затуханием системы пренебречь.

64. В масло опущена гиря массой m = 0,4 кг, подвешенная на спиральной пружине жесткостью k = 40 Н/м. Коэффициент сопротивления r среды r =0,5 кг/с. Вычислить частоту вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна.

65. Определить резонансную частоту ν_рез колебательной системы, если отношение амплитуд первого и шестого колебаний равно 13, а период затухающих колебаний системы составляет 0,2 с.

66. Определить частоту вращения якоря электродвигателя при которой может возникнуть опасность резонанса, если под действием силы тяжести электродвигателя консольная балка, на которой он установлен, прогнулась на h =1,5 мм.

67. Собственной частота колебаний системы ν₀ =10 кГц, резонансная частота на Δν = 2 Гц меньше. Определить логарифмический декремент затухания Λ колебательной системы.

68. Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты в два раза? Коэффициент затухания δ = 0,1ω₀ (ω₀ – циклическая частота собственных колебаний).

69. Амплитуда вынужденных колебаний при неизменной амплитуде вынуждающей силы оказывается одинаковой при частотах ω₁ = 100 с^-1 и ω₂ = 300 с^-1 оказывается одинаковой. Определить резонансную частоту ω_рез.

70. Определить резонансную частоту ω_рез колебаний, если период T ₀ собственных колебаний пружинного маятника равен 0,56 с. Маятник погрузили в упругую среду и период T этого же маятника стал равным 0,57 с.

71. Тело совершает вынужденные колебания в среде с коэффициентом сопротивления r =·10^-3 кг/с. Резонансная амплитуда А _рез равна 5 мм. Частота ν₀ собственных колебаний равна 10 Гц. Определить амплитудное значение вынуждающей силы.

72. Логарифмический декремент затухания Λ колебательной системы равен 0,2. Вычислить резонансную частоту ν_рез системы, если ее собственная частота ν₀ =0,3 кГц.

73. Частота колебаний вынуждающей силы больше резонансной частоты на 15 %. Коэффициент затухания δ равен 0,1ω₀ (ω₀ – циклическая частота собственных колебаний). Определить отношение амплитуды вынужденных колебаний А _вын к резонансной амплитуде А _рез.

74. На пружинный маятник, имеющий циклическую частоту собственных колебаний ω₀ = 115 с^-1, действуют последовательно вынуждающие силы одинаковой амплитуды, но разной частоты F ₁ = 0,5 cos1,9 t и F ₂ = 0,5 cos1,95 t. Жесткость пружины k = 50 Н/м Чему равна амплитуда вынужденных колебаний маятника, происходящих под действием каждой из этих сил?

75. Мальчик несет на коромысле ведра с водой, период собственных колебаний T ₀ которых 1,5 с. При какой скорости движения вода начнет особенно сильно выплескиваться, если длина шага l мальчика равна 0,5 м?

 

76. Определить разность фаз колебаний двух точек, находящихся на прямой, вдоль которой распространяется звуковая волна, и отстоящих друг от друга на 0,5 м. Частота звука 660 Гц, скорость звука 330 м/с.

77. Разность фаз колебаний двух точек, находящихся на прямой, вдоль которой распространяется волна, равна 12,56 рад. Частота звука 660 Гц, скорость волны 330 м/с. Определить расстояние между точками.

78. Волна распространяется в упругой среде со скоростью 300 м/с. Определите период колебаний, если минимальное расстояние между точками среды, фазы колебаний которых противоположны 0,75 м.

79. Поперечная волна распространяется вдоль упругого шнура со скоростью 10 м/с. Период колебаний 2,2 с, амплитуда колебаний точек шнура 7 см. Записать уравнение волны и определить: 1) длину волны; 2) фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии 8 м от источника колебаний в момент времени 3 с.

80. Звуковые колебания, имеющие частоту 300 Гц и амплитуду 0,15 мм, распространяются в упругой среде. Длина волны 80 см. Найти: 1) скорость распространения волн; 2) максимальную скорость частиц среды.

81. Написать уравнение колебаний для точек волны, имеющей скорость распространения 200 м/с, длину волны 50 см и амплитуду 2 см.

82. Найти мощность точечного изотропного источника звука, если на расстоянии 25 м от него интенсивность звука равна 34 . Какова средняя объемная плотность энергии на этом расстоянии?

83. Мощность изотропного точечного источника звуковых волн равна 25 Вт. Определить среднюю объемную плотность энергии на расстоянии 5 м от источника волн. Температуру воздуха принять равной 290 К.

84. Средняя объемная плотность энергии звуковой волны 3 . Определить интенсивность звука, если звук распространяется в сухом воздухе при нормальных условиях.

85. По цилиндрической трубе диаметром 0,2 м и длиной 4 м, заполненной сухим воздухом, распространяется звуковая волна. Найти среднюю за период интенсивностью, если энергия звукового поля, заключенного в трубе 30 мкДж.

86. Плоская звуковая волна имеет период 2 мс, амплитуду 0,5 мм и длину волны 1 м. Для точек среды, удаленных от источника колебаний на расстояние 2 м, найти смещение, скорость и ускорение в момент времени 5 мс. Начальная фаза колебаний равна нулю.

87. Задано уравнение плоской волныx(x,t)= А cos(w t - kx), где A =0,8 см, ω=628 , k =2 . Определить: 1) частоту колебаний и длину волны; 2) фазовую скорость; 3) максимальные значения скорости и ускорения колебаний частиц среды.

88. Плоская звуковая волна возбуждается источником колебаний частоты 100 Гц. Амплитуда колебаний источника равна 5 мм. Написать уравнение колебаний источника ξ(0 ,t), если в начальный момент смещение точек источника максимально. Найти смещение ξ(х, t) точек среды, находящихся на расстоянии 1 м от источника, в момент t =0,1 с. Скорость звуковой волны принять равной 300 м/с. Затуханием пренебречь.

89. От источника колебаний распространяется волна вдоль прямой линии. Амплитуда колебаний равна 0,15 м. Как велико смещение точки, удаленной от источника на , в момент, когда от начала колебаний прошло время t=0,9 Т?

90. Определите длину волны, если числовое значение волнового вектора равно 0, 0157 .

 

91. Белый свет падает нормально на мыльную пленку с показателем преломления n = 1,3, находящуюся в воздухе. Определить наименьшую толщину d _min пленки, при которой отраженный свет с длиной волны λ = 550 нм окажется максимально усиленным на ее поверхности в результате интерференции.

92. Стеклянная плоскопараллельная пластинка толщиной d = 1,3 мкм и показателем преломления n = 1,50 помещена между двумя средами с показателями преломления n ₁ и n ₂. Нормально на пластинку падает свет с длиной волны λ = 600 нм. Определить оптическую разность хода Δ волн, отраженных от верхней и нижней поверхностей пластинки, и указать, усиление или ослабление интенсивности света происходит при интерференции в следующих случаях: 1) n ₁< n < n ₂; 2) n ₁< n > n ₂.

93. Монохроматический свет с длиной волны λ = 0,65 мкм падает под углом 30⁰ на находящуюся в воздухе мыльную пленку (n = 1,33). Определить наименьшую толщину d _min пленки, при которой отраженные световые волны будут максимально ослаблены интерференцией (просветление оптики)?

94. На поверхность стеклянного клина с преломляющим углом γ = 0,2′ нормально падает монохроматический свет с длиной волны λ= 560 нм. Определить ширину b интерференционной полосы.

95. Монохроматический свет с длиной волны λ = 0,60 мкм падает на тонкий стеклянный клин, нормально к его поверхности. Расстояние между смежными интерференционными минимумами в отраженном свете b = 3 мм. Определить угол между поверхностями клина.

96. Стеклянная плоскопараллельная пластинка (n = 1,50) толщиной d = 1,3 мкм помещена между двумя средами с показателями преломления n ₁ и n ₂. Нормально на пластинку падает свет с длиной волны λ = 600 нм. Определить оптическую разность хода Δ волн, отраженных от верхней и нижней поверхностей пластинки, и указать, усиление или ослабление интенсивности света происходит при интерференции в следующих случаях: 1) n ₁ > n < n ₂; 2) n ₁ > n > n ₂.

97. Белый свет нормально падает на мыльную пленку (n = 1,30), находящуюся в воздухе. Определить наименьшую толщину d _min пленки, при которой отраженный свет с длиной волны λ = 650 нм окажется максимально ослабленным в результате интерференции.

98. На тонкий стеклянный клин (n = 1,50) нормально падает монохроматический свет, двугранный угол между его поверхностями g = 1,5′. Определить длину световой волны λ, если расстояние b между смежными интерференционными максимумами в отраженном свете равно 0,4 мм.

99. Белый свет падает под углом 60⁰ на мыльную пленку (n = 1,33). Какой должна быть наименьшая толщина пленки, чтобы отраженные лучи были окрашены в красный цвет (λ = 680 нм)?

100. Вертикальная мыльная пленка (n = 1,33) при стекания жидкости образует клин. При наблюдении интерференционных полос в отраженном свете (λ = 540 нм), оказалось, что расстояние между пятью полосами равно 20 мм. Определить угол клина γ, если свет падает на поверхность пленки нормально.

101. На сколько изменится оптическая длина пути светового пучка, если на его пути поставить стеклянную пластинку толщиной d = 1,2 мм так, что угол падения станет равным i ₁ = 30⁰?

102. Тонкая пленка полимера (n = 1,30) нанесена на стеклянную пластинку. Пластинка освещена параллельным пучком монохроматического света с длиной волны λ = 645 нм, падающим на нее нормально. Определить минимальную толщину d _min слоя, при котором отраженный пучок света имеет наименьшую яркость.

103. Определить длины волн λ лучей видимого света (400≤ λ≤ 800 нм), которые будут ослаблены в результате интерференции, если на пленку (n = 1,47) толщиной d = 1,5 мкм нормально к ее поверхности падает белый свет.

104. Нормально на поверхность воздушного клина падает моно-хроматический свет. Расстояние b между смежными интерференционными максимумами в отраженном свете = 0,42 мм. Как изменится это расстояние, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n = 1,33.

105. Вертикальная мыльная пленка (n = 1,33) при стекания жидкости образует клин. Интерференция наблюдается в отраженном свете через красный светофильтр (λ = 0,630 мкм). Расстояние между соседними максимумами при этом l ₁ = 0,3 см. Затем эта же пленка наблюдается через синий светофильтр (λ = 0,400 мкм). Определить расстояние l ₂ между соседними максимумами. Свет падает перпендикулярно к поверхности пленки и за время измерений форма пленки не изменяется.

106. На стеклянной пластинке лежит выпуклой стороной плосковыпуклая линза. Определить толщину d слоя глицерина (n = 1,47) в том месте, где в отраженном свете (λ = 630 нм) наблюдается первое светлое кольцо Ньютона.

107. На установке для наблюдения колец Ньютона в отраженном свете был измерен радиус третьего темного кольца. Когда пространство между плоскопараллельной пластиной и линзой заполнили жидкостью, то тот же радиус стал у кольца с номером, на единицу большим. Вычислить показатель преломления n жидкости.

108. Определить расстояние Δ r _7,6 между седьмым и шестым кольцами Ньютона, если расстояние между вторым и первым темным кольцами в отраженном свете на этой же установке Δ r _2,1 = 1 мм.

109. Определить расстояние l от двух когерентных источников(λ = 500 нм) до экрана, если расстояние между ними d = 0,2 мм, а расстояние b между первыми интерференционными максимумами на экране 2 см.

110. Диаметры d _i и d _k двух светлых колец Ньютона, у которых порядковые номера не определялись, соответственно равны 4,0 мм и 4,8 мм. Между ними расположено еще три светлых кольца. Определить радиус кривизны плосковыпуклой линзы, взятой для опыта, если кольца наблюдались в отраженном свете с длиной волны λ = 5·10^-7 м.

111. В опыте Юнга расстояние l от щелей до экрана равно 300 см, расстояние d между двумя щелями равно 10^-3 м. Определить длину волны λ, испускаемой источником монохроматического света, если ширина интерференционных полос на экране равна 1,5·10^-3 м.

112. Определите ширину b интерференционных полос на экране, в опыте с зеркалами Френеля, если расстояние d между мнимыми изображениями источника света равно 5·10^-4 м, расстояние l от них до экрана равно 3 м, а длина волны падающего света λ = 0,6 мкм.

113. Кольца Ньютона наблюдаются с помощью двух одинаковых плосковыпуклых линз радиусом R =1,0 м, плотно сложенных выпуклыми поверхностями (плоские поверхности линз параллельны). Определить радиус r ₂ второго темного кольца, наблюдаемого в отраженном свете (λ = 660 нм) при нормальном падении света на поверхность верхней линзы.

114. Плосковыпуклая линза с радиусом кривизны R = 125 мм плотно прижата к стеклянной пластинке. В отраженном свете диаметры десятого и пятнадцатого темных колец Ньютона соответственно равны 1,0 мм и 1,5 мм. Определить длину волны падающего света.

115. На стеклянной пластинке выпуклой стороной лежит плосковыпуклая стеклянная линза(n = 1,6). Радиус третьего темного кольца в проходящем свете (λ = 600 нм) равен 0,9 мм. Найти фокусное расстояние линзы.

116. Установка для получения колец Ньютона освещается светом с длиной волны λ₁ = 579,1 нм, падающим по нормали к поверхности пластинки. Затем мсточник заменили на другой с длиной волны λ₂ = 577 нм. Какое по порядку темное кольцо, соответствующее первой линии совпадает со следующим темным кольцом, соответствующим второй линии? Наблюдение ведется в отраженном свете.

117. Плосковыпуклая стеклянная линза с радиусом кривизны R = 12,5 м соприкасается выпуклой поверхностью со стеклянной пластинкой. При этом в проходящем свете радиус светлого кольца равен r = 2,5·10-3 м. Определить порядковый номер этого кольца, если длина волны падающего света λ = 5,0·10-7 м.

118. Расстояния от стеклянной бипризмы Френеля с преломляющим углом θ = 20′ до узкой щели и экрана равны соответственно а = 0,25 м и b = 1 м. Определить длину волны света, если ширина интерференционной полосы на экране b = 550 мкм.

119. Плосковыпуклая линза соприкасается сферическая поверхностью (R =1м) со стеклянной плоскопараллельной пластинкой. Пространство между пластинкой и линзой заполнено сероуглеродом. Показатели преломления линзы, сероуглерода и пластинки равны соответственно n ₁ = 1,50, n ₂ = 1,63; n ₃ = 1,70. Определить радиус пятого светлого кольца Ньютона в проходящем свете с длиной волны λ = 500 нм.

120. Наблюдение колец Ньютона ведется в проходящем свете. Радиусы двух соседних светлых колец равны r_k = 4,0 мм и r_{k +1} = 4,38 мм. Радиус кривизны плосковыпуклой линзы R = 640 см. Определить длину волны λ падающего света и порядковые номера колец.

121. На щель шириной а = 50 мкм нормально падает монохроматический свет с длиной волны λ = 600 нм. На экране, расположенном на расстоянии L = 1 м, параллельно щели, наблюдается дифракционная картина. Определить ширину центрального дифракционного максимума.

122. Монохроматический свет с длиной волны λ = 690 нм нормально падает на узкую щель шириной а = 50 мкм. Определить угол φ между первоначальным направлением света и направлением на вторую светлую дифракционную полосу.

123. Монохроматический свет с длиной волны λ = 500 нм нормально падает на узкую щель шириной а = 50 мкм. На экране, расположенном на расстоянии параллельно щели, наблюдается дифракционная картина. Определить, максимум или минимум будет наблюдаться на экране под углом φ дифракции равным: 1) 17′; 2) 43′.

124. Определить количество штрихов, приходящихся на каждый миллиметр дифракционной решетки, если при наблюдении в монохроматическом свете (λ = 600 нм), максимум четвертого порядка отклонен на угол φ = 14⁰.

125. На дифракционную решетку, содержащую 200 штрихов на 1 мм, нормально падает монохроматический свет с длиной волны λ=650 нм. Определить, наибольший порядок максимума, который дает дифракционная решетка.

126. Монохроматический свет (λ=0,7 мкм) падает нормально на дифракционную решетку, содержащую 300 штрихов на 1 мм. Вычислить общее число дифракционных максимумов, которые дает эта решетка и угол φ дифракции, соответствующий максимуму наибольшего порядка.

127. На дифракционную решетку, содержащую n =10⁵ штрихов на 1 м, падает нормально монохроматический свет. На максимум наведена зрительная труба спектрометра. Угол, между максимумами третьего порядка равен Δφ=25°. Определить длину волны λ падающего на решетку света.

128. На дифракционную решетку нормально падает белый свет. Спектры шестого и четвертого порядков перекрывают друг друга. Определить длину волны в спектре четвертого порядка на которую накладывается фиолетовая граница (λ=0,4 мкм) спектра шестого порядка?

129. Под углом α=60° на дифракционную решетку с периодом d =20 мкм падает свет с длиной волны λ=500 нм. Определить угол φ дифракции, соответствующий третьему главному максимуму?

130. Нормально к поверхности дифракционной решетки, содержащей n =400 штрихов на 1 мм, падает белый свет. Образующийся спектр проецируется линзой, помещенной вблизи решетки, на экран. Определить ширину b спектра второго порядка на экране, если расстояние L от линзы до экрана равно 2 м. Границы видимости спектра λ_кр=780 им, λ_Ф=400 нм.

131. Параллельный пучок лучей монохроматического света (λ=0,4 мкм) падает нормально на

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: