Общая постановка задачи дискретизации

В самом общем случае представление непрерывного сигнала и(t) на интервале Т совокупностью координат может быть записано в виде

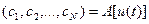. (4.2)

где А — оператор дискретного представления сигнала, реализуемый устройством, называемым дискретизатором.

Аналогично можно записать и операцию восстанов­ления по совокупности координат непре­рывной функции (воспроизводящей функции), отображающей исходный сигнал с некоторой текущей погрешностью приближения :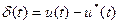

(4.3)

где В — оператор восстановления, реализуемый устройст­вом восстановления сигнала.

Задача дискретизации в математическом плане сво­дится к совместному выбору пары операторов А и В, обеспечивающих заданную точность восстановления сиг­нала.

Рассмотрим разновидности используемых операторов A и В и критериев оценки точности восстановления сигнала.

Широкое практическое применение нашли линейные операторы, поскольку их техническая реализация проще. Для определения координат сигнала используется со­отношение

(4.4)

где — система функций, которые для определен­ности назовем весовыми.

Воспроизводящая функция представляется аппрокси­мирующим полиномом

, (4.5)

где 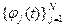— система базисных функций.

При одном и том же операторе представления А для восстановления могут использоваться различные операторы В.

Из соотношений (4.4) и (4.5) следует, что произведения 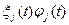должны иметь размерность, обратную времени.

Методы дискретизации следует рассматривать как с позиций полезности для решения теоретических вопросов передачи и преобразования сигналов, так и с позиций возможности их технической реализации. В теоретическом плане весьма важны методы дискретизации, обеспечивающие минимальное число координат при заданной погрешности воспроизведения. Их называют методами оптимальной или предельной дискретизации.

Широкое распространение получили методы дискретизации, при которых сигнал u(t) заменяется совокупностью его мгновенных значений ,взятых в определенные моменты времени и назы­ваемых выборками или отсчетами. Роль весовых функций 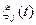в соотношении (4.4) в этом случае выполняют дельта-функции Дирака. В соответствии с (3.5) устанавливаем, что координаты 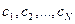представляют собой выборки или разности соседних выборок

Поскольку дельта-функция технически нереализуема, длительность каждой выборки конечна. Отсчеты берут не в одной точке, а в некотором интервале времени, зависящем от длительности управляющего импульса ключевого устройства. Когда длительность импульса значительно меньше шага дискретизации, выборки представляют собой короткие импульсы, амплитуды которых пропорциональны мгновенным значениям сигнала.

Отрезок времени 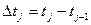между соседними выборками называют шагом дискретизации. Если он выдерживается постоянным во всем диапазоне преобразования, дискретизация считается равномерной. Методы равномерной дискретизации получили наиболее широкое применение. Они характеризуются простым алгоритмом, исключающим необходимость фиксировать время отсчетов, что существенно облегчает техническую реализацию. Правда, в этом случае несоответствие шага дискретизации характеру поведения конкретной реализации сигнала на отдельных участках часто приводит к значительной избыточности отсчетов.

Если отрезки времени между выборками меняются, например, в зависимости от скорости изменения сигнала или по заданной программе, дискретизацию называют неравномерной.

В ряде случаев наряду с выборками в качестве координат сигнала используются также производные u(t) в те же моменты времени 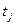вплоть до N -гo порядка.

Учитывая теоретическую и практическую значимость методов дискретизации с использованием выборок в качестве координат сигнала, в процессе дальнейшего рассмотрения вопросов дискретизации ограничимся только ими.