Равномерная дискретизация. Теорема Котельникова

Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром в наиболее четкой форме сформулировано и доказано акад. В.А.Котельниковым в виде теоремы, получившей в отечественной литературе его имя.

При дискретизации по времени непрерывная по аргументу функция, описывающая сигнал, преобразуется в другую, решетчатую функцию, образованную путем прерывания исходной функции (рис. 4.1б). Дискретизация допустима при условии, что новообразованная решетчатая функция дает возможность восстановить исходную функцию. Естественно, что такая замена допустима лишь в тех случаях, когда дискретизированная функция полностью представляет исходную.

Итак, в результате дискретизации исходная функция x (t) заменяется совокупностью отдельных значений (отсчетов), т.е. решетчатой функцией x (k∆t), где k – номер отсчета, k = 1, 2, 3, …. Каким должен быть интервал Δ t между отдельными отсчетами? При малом интервале между отсчетами их количество будет больш и м и точность последующего восстановления функции также будет высокой. Если же интервал между отсчетами взять большим, то количество отсчетов уменьшится, однако погрешность восстановления непрерывного сообщения может оказаться больше допустимой. Оптимальным следует считать такой интервал между отсчетами, при котором исходная функция с заданной точностью представляется минимальным числом отсчетных значений. В этом случае все отсчеты будут существенными для восстановления исходной функции. При большем числе отсчетов будет иметь место избыточность информации.

Способ дискретизации, согласно которому выбираются отсчеты или коэффициенты разложения, целесообразно оценивать по величине ошибки восстановления исходной функции. Различают три вида кри­териев отсчетов:

1. Частотный критерий Котельникова, согласно которому интервалы между отсчетами выбираются исходя из ширины спектра дискретизируемого сообщения.

2. Корреляционный критерий отсчетов Железнова, согласно которому интервал дискретизации выбирается равным времени корре­ляции передаваемого сообщения.

3. Квантовый критерий отсчетов Темникова, предложенный для детерминированных функций, устанавливающий зависимость интервалов между отсчетами от величины ступени квантования по уровню и крутизны функции. Оценку точности восстановления непрерывного сообщения можно производить по величине наибольшего, среднеквадратично­го или интегрального отклонения.

Теорема Котельникова. Все реальные непрерывные сообщения отражают процессы, основная часть спектра которых сосредоточена в конечном интервале частот. Это объясняется частотными свойствами источников сообще­ний и абонентов (получателей сообщений), являющихся реальными физическими системами. Начиная с некоторой частоты, высокочастотные со­ставляющие спектра сообщения оказываются значительно ниже уровня помех и не воспринимаются получателем. В таком случае все реальные непрерывные сообщения можно рассматривать как функции с ограниченным спектром, т. е. таким, в котором не содержится частот выше некоторой граничной частоты F.

В инженерной практике рассмотрение сигналов как функций с ограниченным спектром позволяет при проектировании аппаратуры связи ограничивать ее полосу пропускания. Так на практике часто сталкиваются со следующими примерными значениями ширины спектра сигналов в каналах связи: телеграфного – несколько сотен герц (в зависимости от скорости телеграфирования), телефонного – 3-5 кГц, вещания – 8-10 кГц, телевизионного – порядка 6 МГц.

Для таких функций В.А. Котельников сформулировал следующую теорему:

Любая непрерывная функция со спектром, находящемся в интервале (0, F), полностью определяется последовательностью ее значений в точках, отстоящих на 1/2F секунд друг от друга.

 

Доказательство теоремы Котельникова основано на разложении функции х (t)с ограниченным спектром в ряд. Спектр S (j ω) рассматриваемой функции ограничен полосой ω_в = 2π F _в,т.е.

(4.13)

Используя преобразование Фурье непрерывной функции

.

(4.14)

и (4.13) получим

(4.15)

Рассмотрим комплексный спектр функции х (t).Он задан на интервале (–ω _B, ω _B) и может быть представлен рядом Фурье

,

(4.16)

где

.

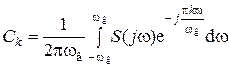(4.17)

 

Сравнивая (4.17) и (4.15, получаем

(4.18)

Подставив значение C_k в (4.16), будем иметь

.

(4.19)

 

Уже это соотношение доказывает теорему Котельникова: так как между x (t) и S (jω) имеется однозначная связь, то x (t), как и S (jω) (см. (4.19)), однозначно определяется отсчетами { x (k ∆ t)}.

Выразим функцию х (t)через ее спектр, используя (4.15)

(4.20)

Учитывая сходимость ряда и интеграла Фурье, произведем пере­становку операций интегрирования и суммирования:

.

(4.21)

Определив значение интеграла

 

 

и подставив его в (4.21), окончательно получаем выражение, называемое рядом Котельникова:

(4.22)

Полученное выражение представляет собой разложение в ряд непрерывной функции х (t).Величины х (k Δ t) – значения непрерывной функции в точках отсчета. Множитель вида

(4.23)

является функцией времени и называется функцией отcчетов (рис. 4.2).

Рис.4.2. График функции отсчетов

 

Функция отсчетов принимает максимальное значение, равное еди­нице, в моменты времени t = k Δ t и обращается в нуль в моменты вре­мени t = (k ± т)Δ t, где т = 1, 2, 3,... Следует отметить, что функции отсчетов ортогональны на бесконечно большом интервале времени. Функция отсчетов представля­ет собой реакцию идеального фильтра нижних частот на единичную импульсную функцию.

Таким образом, чтобы передать сообщение, являющееся непрерыв­ной функцией времени и имеющее ограниченный спектр, необходимо произвести следующие операции:

1. Найти отсчетные значения передаваемого сообщения в моменты времени, разделенные интервалами Δ t = 1/2 F _в.

2. Передать величины отсчетов по каналу связи любым из возможных методов.

3. Восстановить на приемном конце переданные отсчеты и сфор­мировать импульсы с малой длительностью (по сравнению с интерва­лом между отсчетами), амплитуды которых были бы равны передан­ным отсчетным значениям.

4. Сформировать функции отсчетов с амплитудами, равными амплитудам переданных отсчетных значений.

5. Просуммировать функции отсчетов и получить функцию времени, которая равна (или пропорциональна) переданному сообщению. Совокупность приведенных операций представлена на рис. 4.3.

х (t)

х (3Δ t)

х (Δ t) х (5Δ t)

t

Δ t 2Δ t 3Δ t 4Δ t

k= 1 t

k= 2

2 t

 

k= 3

3 t

k= 4

t

k= 5

5 t

 

Рис. 4.3. Восстановление непрерывной функции

 

Теорема Котельникова справедлива и для случая, когда непрерывное сообщение х (t)имеет спектр, заключенный в ограниченной полосе частот от f _н до f _в. В этом случае отсчеты следует брать через интервал времени

(4.24)

 

где Δ f _сп – ширина спектра функции, Δ f _сп = (f _в – f _н).

 

Строго говоря, условия теоремы Котельникова для реальных сигналов не удовлетворяются, поскольку они представляют процессы, ограниченные во времени, и поэтому их спектр не ограничен. Однако практически всегда можно ограничить сверху спектр реального сигнала достаточно большой частотой F _втак, чтобы составляющие спектра за ее пределами были незначительными.

Таким образом, учитывая отмеченные ранее особенности реальных сообщений (сосредоточенность почти всей энергии в конечных интервалах времени и полосы частот), выражение (4.22) можно с достаточной степенью точности использовать для представления реальных сообщений. В этом случае при длительности сообщения Т _счисло отсчетов m будет конечным

(4.25)

а (4.22) примет вид

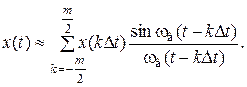
(4.26)

 

При конечном числе отсчетов сумма (4.26) будет совпадать с мгновенными значениями х(t) не на всем интервале существования сообщения Т _с,атолько в отсчетных точках. В промежутках между этими значениями х (t)отличается от суммы конечного числа членов ряда, в результате чего возникает погрешность. Эта погрешность ми­нимальна в середине интервала Т _си будет возрастать к его краям.

Определить среднеквадратичную ошибку восстановления сообщения конечной длительности рядом Котельникова с конечным числом членов затруднительно. Однако, если убывание модуля спектральной плотности происходит достаточно быстро, можно указать границы среднеквадратической ошибки d, возникающей при восстановлении реального сообщения с неограниченным спектром рядом Котельникова (4.22) в следующем виде:

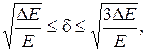
(4.27)

 

где Е – полная энергия сообщения,

(4.28)

 

а Δ E – энергия сообщения, заключенная в полосе частот выше

(4.29)

 

С помощью оценки (4.29) можно определить F _втаким образом, чтобы по­грешность восстановления непрерывного сообщения не превышала за­данной величины.

В практических расчетах для определения относительной погрешности воспроизведения сообщений может быть использовано следующее выражение:

(4.30)

позволяющее по заданной величине δ при известных спектральных характеристиках сообщения найти верхнюю граничную частоту спектра ω_в и интервал дискретизации

.

(4.31)

 

Как видно на рис. 4.3, для воспроизведения исходной функции х (t)по ее дискретным значениям x (k D t)необходимо устройство с импульсной реакцией вида (4.23). На выходе такого устройства и будет воспроизводиться исходная непрерывная функция x (t).

Подобную импульсную реакцию имеет идеальный фильтр нижних частот с частотой среза F. Таким образом, непрерывная функция может быть восстановлена при пропускании последовательности импульсов вида x (k D t)d(t–k D t)(решетчатой функции) через идеальный фильтр нижних частот с указанной частотой среза. Здесь d(t–k D t)– дельта-функция. Практически эти импульсы аппроксимируются, например, прямоугольными импульсами длительностью D, где D << D t, и высотой x (k D t)/D.

Ясно, что отклонение свойств ФНЧот идеального ведет к некоторым искажениям в воспроизведении непрерывного сигнала по его дискретным отсчетам.

В заключение заметим, что, хотя не существует реальных сигналов со строго ограниченным спектром, это не умаляет практического значения выводов, сделанных из теоремы Котельникова. Принимая сигнал с практически ограниченным спектром (что всегда имеет место на практике) за идеальный сигнал со строго (в смысле условий теоремы) ограниченным спектром, мы после восстановления по дискретным отсчетам получим сигнал, несколько отличный от исходного, но это отличие незначительно, если правильно выбрана ограничивающая спектр частота F. В процессе передачи сигнал дополнительно искажается различными помехами, и на их фоне можно пренебречь искажениями, вызванными отличием реальных сигналов от идеальных.

 

Принцип дискретизации Железнова. В предложенной Железновым модели сообщения характеризуются: конечной длительностью Т _с; сплошным спектром, отличным от нуля на всей частотной оси, т.е. S (ω) ¹ 0 при – ¥ < ω < ¥.

Вводится допущение ограниченности интервала корреляции (т.е. считается, что функция корреляции равна нулю вне интервала τ₀) и малости интервала корреляции по сравнению с длительностью сообщения (Т _с>> τ₀). Рассматриваются сообщения, являющиеся стационарными и нестационарными функциями времени. Введенные допущения не вступают в противоречие с природой реальных сообщений, так как вследствие конечной длительности их значение в любой момент зависит только от некоторого отрезка прошлого ограниченной длительности. Поэтому интервал корреляции реальных сообщений является ограниченной величиной. Это ограничение, записываемое в виде

(4.32)

 

представлено на рис. 4.4.

 

Рис. 4.4. Ограничение интервала корреляции

Рис. 4.5. К определению эффективной полосы частот

 

Н.А. Железновым доказано, что такие сообщения могут быть предсказаны системой линейного прогнозирования со среднеквадратичной ошибкой, сколь угодно мало отличающейся от нуля, только в промежутке времени, равном интервалу корреляции τ₀. Таким образом, дискретизацию следует производить с интервалом, не превышающим τ₀, поскольку лишь в этом случае возможно безошибочное восстановление исходного сообщения. Число некоррелированных отсчетов N при этом определится так

(4.33)

 

Определение интервала корреляции τ₀ производится с использованием понятия эффективной полосы частот сообщения

,

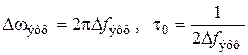(4.34)

где Δω_эфф определяется как основание прямоугольника с высотой, равной максимальному значению спектральной плотности S_x (ω), и площадью, равной площади под кривой спектральной плотности сооб­щения (рис. 4.5):

.

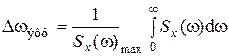(4.35)

 

Для нестационарных функций используется понятие текущего интервала корреляции, который является функцией времени τ₀ = τ₀(t).В этом случае отсчетные значения непрерывного сообщения будут располагаться на оси времени неравномерно. Метод дискретизации Н.А. Железнова менее разработан, чем метод В.А. Котельникова, и поэтому не получил еще широкого распространения.

 

Адаптивная дискретизация

 

Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множество возможных реализаций сигнала и потому опирались на предельные значения его динамических характеристик, то при адаптивной дискретизации мы ориентируемся на динамические характеристики конкретной реализации, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью.

В основе принципа адаптивной дискретизации лежит непосредственное слежение за текущей погрешностью восстановления сигнала .

Наиболее широкое применение на практике получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. В процессе последовательного наращивания интервала аппроксимации производится сравнение сигнала u(t) с воспроизводящей функцией ,формируемой с учетом текущих значений динамических характеристик сигнала. Когда погрешность воспроизведения достигает заданного значения 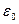, наращивание интервала прекращается и производится отсчет. Интервалы времени между отсчетами при этом оказываются произвольными.

В качестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы (4.6) нулевой и первой степеней. При этом возможны как интерполяционные, так и экстраполяционные способы адаптивной дискретизации. Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации и выполнением большого числа вычислительных операций. Поэтому ограничимся рассмотре­нием примеров адаптивной дискретизации на основе экстраполяции.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: