 |
Механические характеристики основного центробежного насоса
|
|
|
|
Центробежный насос по данным относится к механизмам с механической характеристикой. В то же время по тем же источникам нет математического описания поведения насоса в начальный период пуска. Установить характер поведения насоса, уточнить зависимость между моментом и скоростью вращения рабочего колеса насоса, посвящен этот раздел диссертационной работы. Теоретические и экспериментальные исследования в совокупности с принятой моделью позволяют предложить методику расчета механической характеристики насоса. В соответствии с моделью и используя условие изогональности работы реального и фиктивного насосов, правомерно предположить, что в данном случае выполняются условия кинематического подобия обоих насосов, из которого следует
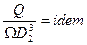(2.7)
где Q - подача насоса (м3/с);
Ω - угловая скорость вращения рабочего колеса насоса (рад/с);
D2 - внешний диаметр рабочего колеса (м).
Для определения параметров фиктивного насоса необходимо определить теоретическое значение подачи насоса, которая определится [64]:
, (2.8)
где 
- теоретическая подача насоса м^/с;
- номинальная подача насоса м^/с;
- коэффициент сужения выходного патрубка насоса;
- объемный кпд, который в соответствии с [11] определится:
(2.9)
где ns - коэффициент быстроходности насоса;
Действительная подача отличается от теоретической вследствие того, что происходит сужение выходного отверстия рабочего колеса, так как лопатки реального насоса имеют конечную толщину. Уменьшение сечения потока жидкости происходит на величину (s1 b2 z).
Пользуясь рекомендациями [4] коэффициент сужения выходного сечения может быть определен:
|
|
|
(2.10)
где 
- ширина рабочего колеса на выходе потока (м);
z - число лопаток рабочего колеса насоса;
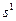- толщина лопаток на выходе, замеренная вдоль окружности (м).
Кроме того, в реальном насосе подача уменьшается из-за наличия зазоров и неплотностей между рабочим колесом и корпусом в сальниковых уплотнениях. Коэффициент быстроходности находится на основании теории подобия и может быть представлен [51, 54, 58]
(2.11)
где n -скорость вращения рабочего колеса насоса (об/мин).
Зная теоретическую и номинальную подачу насоса легко определить составляющую фиктивной подачи насоса как разность
(2.12)
Рассматривая механизм возникновения движения жидкости в насосе, следует иметь ввиду, что кроме поступательного движения существует еще и циркуляционное, которое направлено противоположно основному потоку. Его можно учесть, определив расчетную подачу
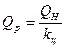(2.13)
где 
- коэффициент циркуляции, используется как поправка к основному уравнению насосов и учитывает конечное число лопаток насоса.
Коэффициент циркуляции может быть определен по формуле академика Проскуры Г.Ф. [58]
(2.14)
или
где коэффициент 
z - число лопаток рабочего колеса насоса;
, 
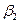- углы входа и выхода потока жидкости в рабочее колесо насоса;
D1 - внутренний диаметр рабочего колеса (м);
R1 и R2 - внутренний и внешний радиусы рабочего колеса насоса (м).
Для практических целей рекомендуется [51] коэффициент в виде:
, (2.15)
где коэффициент (0,55 - 0,65) зависит от шероховатости поверхности проточной части колеса. Для тщательно обработанных колес можно принять нижний предел.
Разность между расчетной и номинальной подачами определит вторую
составляющую расхода фиктивного насоса
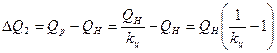(2.16)
При этом принято считать [58,64], что до возникновения подачи насоса за пределы своего корпуса, имеет место циркуляционное движение жидкости и расход ΔQ2 замыкается во внутренней полости насоса и движется в направлении, обратном направлению движения основного потока. Таким образом, расход фиктивного насоса, согласно принятой модели, будет представлять собой сумму расходов, определяемых выражениями (2.12) и (2.16)
|
|
|
(2.17)
Принятая модель представления центробежного насоса предполагает соблюдение между реальным и фиктивным насосом условия изогональности, в соответствии с [5]
(2.18)
Из (2.18) определяется 
:
(2.19)
Принятое условие изогональности работы основного и фиктивного насосного агрегата [5,51,54,58] позволяет записать:
(2.20)
Выражение (2.20) позволяет определить напор фиктивного насоса
(2.21)
Из условия энергетического подобия [5] режимов следует:
(2.22)
(2.23)
Анализ и обработка отечественных и зарубежных каталожных данных центробежных насосных агрегатов позволяет утверждать, что пусковая характеристика центробежного насоса представляет собой параболическую зависимость, вершина которой смещена относительно начала координат. Такое предположение подтверждает классическая теория насосостроения, согласно которой центробежные насосы относятся к разряду нагрузки с вентиляторным моментом на валу. Проведённые теоретические и натурные исследования на насосных станциях позволили предложить описание пусковой характеристики центробежного насоса выражением вида:
(2.24)
где М - момент сопротивления, развиваемый центробежным насосом;
- момент трогания насосного агрегата;
х,у - коэффициенты аппроксимации механической характеристики насоса.
Экспериментально снятые пусковые характеристики центробежного насоса (рисунок 2.3) подтверждают теоретические предпосылки о том, что насос при пуске не сразу захватывает воду и развивает производительность, а вначале рабочее колесо как бы "проскальзывает".Это объясняется тем, что для образования циркуляционных потоков, то есть для образования установившегося режима обтекания профиля с некоторой величиной присоединённого вихря требуются затраты энергии и времени на образование начальных вихрей, а образующаяся турбулентность требует от насоса всё большей энергии для приведения жидкости в движение.
|
|
|
Крутящий момент в рабочем колесе создается только в том случае, когда оно воздействием своих лопастей меняет циркуляцию потока. Циркуляция. При этом, является мерой закрученности потока. В этом случае преобразование подведенной к насосу механической энергии в гидравлическую осуществляется в рабочем колесе за счет взаимодействия потока с лопастями рабочего колеса, представляющего собой вращающуюся решетку профилей. По мере того, как жидкость, проходящая через рабочее колесо, приобретает идеальный угол (приближается к проектному ), насос развивает номинальные значения подачи и напора. Отсюда следует, что при достижении рабочим колесом насоса минимальной частоты вращения 
устанавливаются устойчивые циркуляционные потоки внутри насоса, и дальнейшее поведение насоса описывается параболой с вершиной в точке , 
Одна из координат, вершины которой определена (2.19) и может быть получена из (2.24) в виде:
, (2.25)
а вторая координата, определится в соответствии с
. (2.26)
Выражение (2.24) графически изображается параболой вида
(2.27)
вершина, которой лежит не в начале координат, а в точке с координатами, определенными выражениями (2.25), (2.26).
В соответствии с (2.27), коэффициент "у", определится из условия номинального режима:
. (2.28)
Коэффициент "х" выражения (2.24), определится
-
(2.29)
Момент трогания в выражении (2.24) определится из условия работы в номинальном режиме
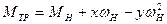(2.30)
Таким образом, определены все величины и характерные точки, определяющие местоположение зависимости (2.24).
Практическое значение механической характеристики центробежного насоса состоит в том, что она позволяет:
а) Определить момент трогания насосного агрегата и по нему судить о качестве
ремонта, как профилактического, так и капитального;
б) Обеспечить пуск насосного агрегата в энергосберегающем режиме.
Для обеспечения нормальной и экономичной работы насосных установок необходимо контролировать состояние зазоров между уплотнительным кольцом и рабочим колесом насоса, а также степень затяжки сальниковых уплотнений [50]. Это важно потому, что как слабая затяжка, так и перетяжка сальниковых уплотнений ведут к неоправданному завышению потребляемой электроэнергии на перекачку жидкости. Контролировать состояние сальниковых уплотнений после профилактических и капитальных ремонтов позволяет знание величины момента трогания 
соответствии с выражением (2.30). На рисунке 2.4 представлена пусковая характеристика насоса MF 50-50, рассчитанная по формуле (2.24).
|
|
|
|
|
|
