Правило формирования дерева графа.

1) В дерево графа входят ветви, содержащие источники напряжения; управляемые и неуправляемые; ёмкости

2) В дерево графа не входят ветви, содержащие источники тока, управляемые и неуправляемые; индуктивности

3) Сопротивления могут входить, если не образуют замкнутый контур и не входят, если контур замыкают

 

Ветвь, входящая в дерево графа, получила название ребра. Ветвь не входящая в дерево графа – хорда.

5. Модель Эберса-Молла (полупроводниковый диод, транзистор).

 

Дифференциальное сопротивление эмиттера составляет единицы – десятки Ом, сопротивление объема базы – сотни Ом, сопротивление коллектора в схеме с ОБ – Мегомы. Емкость коллекторного перехода составляет единицы – десятки пикофарад. В схеме с ОЭ в выходной цепи дифференциальное сопротивление и емкость.

 

6. Матрица главных сечений: формирование, связь с токами и напряжениями, назначение.

 

Одна из топологических моделей

МГС – матрица главных сечений, она формируется на основе закона Кирхгоффа для токов главных сечений или закона Кирхгоффа для напряжений – хорд.

На практике этот метод не применяется. Если дерево графа и его дополнение рассечь замкнутой линией, пересекающей ветвь графа не более одного раза, то эта линия будет называться сечением.

Главное сечение – сечение, пересекающее лишь одно ребро, количество пересекаемых хорд может быть любым.

Для каждой схемы может быть построено 5 главных сечений по числу рёбер.

Составим закон Кирхгоффа для главных сечений. Сумма токов, втекающих в главное сечение равна 0.

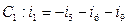
Перейдём к матричной форме записи, оставив в левой части токи рёбер, а в правой – токи хорд. Если вынести минус перед матрицей, то F – матрица главных сечений.

 

Можно связать токи рёбер и токи хорд. Аналогично можно получить матрицу главных сечений на основе управлений Киргоффа для напряжений хорд.

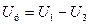
Если преобразовать систему уравнений так, чтобы слева находились напряжения хорд, а слева напряжения рёбер, то матрица, связывающая эти напряжения, будет транспонированной:

 

- вектор напряжения хорд

- вектор напряжения рёбер

Зная матрицу главных сечений можно связать между собой:

1) токи рёбер и токи хорд

2) напряжение хорд и напряжение рёбер

На практике матрицу главных сечений получают исходя из матрицы инциденций: на основе методов линейной алгебры. Матрица инциденций - матрица связи или матрица структуры.

 

7. Матрица инциденций: назначение, пример формирования.

Матрица инциденций содержит информацию о соединениях узлов и ветвей. Элемент матрицы , где i – номер узла, а j – номер ветви. Причём, ветвь либо входит в узел, либо выходит из узла, либо подсоединена к узлу.

 

0, если j-я ветвь не подсоединена к узлу

= +1, если j-я ветвь выходит из узла

-1, j-я ветвь входит в i-ый узел

 

Сформировать матрицу инциденций можно:

на основе графа схемы

на основе схемы, подготовленной для построения графа (нумерацию узлов, нумерацию ветвей, направление ветвей).

Размерность матрицы инциденций определяется количеством узлов и ветвей в схеме:

Целесообразно заполнить матрицу с учётом того, что ветвь выходит из одного узла и входит лишь в один узел, т.е. заполнить по столбцам матрицу. Если проанализировать матрицу, то наблюдается закономерность в столбцах: одна единица, одна (-1), остальные нули. В связи с этим одну строчку из матрицы без потери информации можем отбросить. Принято отбрасывать нижнюю строку.

Матрица инциденций, содержащая все строки, называется полной матрицей инциденций. Матрица без одной строки – редуцированной матрицей или структурной матрицей. Структурная матрица связывает все токи ветвей.

Имеем закон Киргоффа для ветвей.

Если от последнего соответствия перейти к соотношению вида , выделив в левую часть токи рёбер, то получим матрицу главных сечений.

Вывод: топологические модели(все их 4 формы) связаны между собой и предназначены для формирования на их основе топологических уравнений.

 

Три вида топологических уравнений:

1) для уравнений токов, рёбер и хорд

2) для уравнений напряжений

3) матрицы

 

Формирование математической модели происходит на основе топологических и компонентных уравнений. Компонентные уравнения – уравнения, устанавливающие связи между токами и напряжениями на отдельных компонентах.

Рассмотренное формирование математической модели соответствует моделям цепей в пространстве состояний. Применение иных моделей цепей матричная форма для линейных цепей в частотной области или описание нелинейных цепей на основе функциональных рядов предполагает иные алгоритмы формирования математической модели.

Если необходимо промоделировать нелинейную цепь, то для описания нелинейных элементов(диодов, транзисторов) используется эквивалентные схемы, содержащие R,L,C – элементы, источники тока, напряжения, в том числе нелинейные и управляемые.

 

8. Метод переменных состояний: структура схемы, вид уравнений для линейной цепи без особенностей.

Дана схема, содержащая R, L, C – элементы, источники напряжения и тока.

1) Схема не содержит управляемых источников.

2) Не является схемой с особенностями, контуров из ёмкостных элементов и сечений из индуктивных элементов и источников тока.

Преобразуем схему, вынеся за пределы:

1) Независимые источники.

2) Реактивные элементы.

3) Выходные клеммы.

X(t)

U_C I_L

 

 

U_C1(t) U_C1(t)

 

 

I i₁(t) U_вых(t)

 

 

X_ни(t) U_вых(t)

 

U U₁(t) i_вых(t)

 

вектор независимых источников объединяет вектор независимых источников напряжений и вектор независимых источников тока.

вектор состояний объединяет вектора на ёмкостных элементах и вектора тока и индуктивностях. может быть либо током, или напряжением.

Внутри R-цепи получится резистивный пассивный многополюсник. Для него справедлив принцип суперпозиций и можно установить соотношение между токами резистивных элементов, векторов независимых источников и вектором состояний.

I_рез(t) – вектор токов резистивных элементов.

 

B₁,B₂ – матричные коэффициенты, значения которых определяются.

1) Топологией резистивной цепи.

2) Полиномами или значениями сопротивлений.

Размерность B₁ определяется:

1) Число строк = числу резистивных элементов.

2) Число столбцов = количеству реактивных элементов.

Размерность B₂ определяется:

1) Число строк = числу резистивных элементов.

2) Число столбцов = числу источников.

Соотношение между токами и напряжениями на реактивных элементах и напряжениями (токами в узлах многополюсника)описываются с помощью уравнений состояния:

(2)

 

Где X(t) – напряжение на ёмкостях и токи в индуктивностях

;

;

 

Из полученных уравнений для емкостей и индуктивностей следует, что матричные коэффициенты и определяется.

1) Структурой схемы.

2) Полиномами R, L, C – элементов, их размерность определяется : квадратная матрица число строк, число столбцов равно числу реактивных элементов. -число строк равно количеству реактивных элементов, число столбцов равно числу источников.

 

Связь между векторами выходных параметров и напряжениями и токами в резистивном многополюснике отображается уравнением выхода (3)

 

Здесь и - матричные коэффициенты, значения элементов которых определяется:

1) Топологией схемы.

2) Значениями сопротивлений.

(4)

Замечание: элементы матричных коэффициентов являются действительными числами. Пример их формирования можно посмотреть в Калабенове.

 

При решении задач анализа известны:

1) Значения матричных коэффициентов

2) Вектор независимых источников X_нч(t).

3) Начальные условия: напряжение на ёмкостях и токи в индуктивностях в момент t=0.

Определить:

1) .

2) I_рез – вектор токов резистивных элементов.

3) I_вых(t).

 

Последовательность решения систем уравнения определяется соотношением числа уравнений и количество неизвестных.

 

1 система уравнений число уравнений = числу резистивных элементов. Количество неизвестных = числу резистивных элементов в + число реактивных элементов.

Число неизвестных > количество уравнений => систему однозначно решить нельзя.

 

Уравнение системы: число уравнений = количеству выходных напряжений и токов. Количество уравнений – размерность выходного вектора X_вых+X – размерность.

3-е уравнение однозначно решить не можем.

2-е уравнение (2 система уравнений).

 

Количество уравнений = количеству неизвестных и определяется числом реактивных элементов. Данное уравнение решается численными методами на основе рекуррентных соотношений

9. Метод переменных состояний: структура схемы, вид уравнений для цепи с нелинейными реактивными элементами.

 

Преобразуется исходную схему, содержащую R, C, L, C(), L(), U(t), i(t) к виду, аналогичному преобразованной цепи с линейными элементами.

X(t)

 

U_C(t) U_C(t) U_C(t) U_C(t)

 

Формально математическая эквивалентная схема описывается системой уравнений вида: 1, 2, 3.

При этом размерность вектора X(t) определяется числом реактивных элементов линейных + нелинейных.

Отличие модели в матричные коэффициенты - становятся зависимым от времени.

, (i=1,2), где

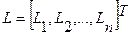
- для нелинейных ёмкостей.

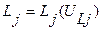- для нелинейных индуктивностей.

Мгновенные значения напряжения на нелинейной области и тока через нелинейную индуктивность.

Пр. C- барьерная ёмкость.

 

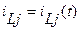
Ai – функция от C_L – функция от времени.

- функция от времени;

В каждый момент времени имеет своё значениё.

Зависимость матричных коэффициентов накладывает ограничение на процедуру решения системы уравнения (2)

Известно:

1) X незав. источника в (t).

2)

3)

Найти:

1)

2)

Один из алгоритмов решения:

Допуская, что изменение матричных коэффициентов на шаге интегрирования ДУ.

Обозначим через незначительно.

(i=1,2)

В связи с этим при расчете по регулярным соотношениям берём значение A_i предыдущего шага. После расчёта на очередном шаге производим пересчет . Анализ схемы в данном случае является более трудоемким, чем для схемы с линейными параметрами

 

 

10. Метод переменных состояний: структура схемы, вид уравнений для цепи с нелинейными резистивными элементами

Любую схему, содержащую R, L, C нелинейные элементы можно свести к схеме с нелинейными без инерционными элементами.

Дана схема содержащая R, L, C – элементы.

R, R(), L, C, U(), i().

Преобразуем данную схему, оставив линейный многополюстник.

 

U_C(t) …… i_L(t)

 

……

 

 

В эквивалентной схеме изменилась размерность резистивного многополюстника, добавились выходы, к которым подключены нелинейные элементы. Напряжения и токи на входе нелинейных элементов обозначим через:

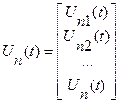
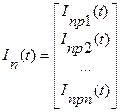
Тогда структура математической модели имеет вид:

(1’)

(2’)

При решении задачи анализа в системе уравнений число уравнений равно числу реактивных элементов; число неизвестных равно число реактивных элементов + число нелинейных резистивных элементов. Следовательно, необходимо увеличить количество уравнений для разрешимости системы.

Введём уравнение нелинейных резистивных:

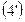, где

- матричные коэффиценты определяются:

1) топологией схемы и значениями линейных резистивных сопротивлений

Совместное решение системы и 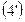позволяет определить неизвестные и

Система уравнений 1-3 предполагают запись в явном виде относительных по произведённых по направлению или току на реактивных элементов. Это является признаком модели в пространстве состояний.

Если производственная в явном виде не выражена, а входит в качестве аргумента в состав некоторых функций, то модель содержит производственные, но не является модельно в пространстве состояний.

Решение ДУ осуществляемые численными методами ориентировано на явное выражение производных(на модели в пространстве состояний).

 

11. Метод переменных состояний: решение систем дифференциальных уравнений (явные и неявные методы, порядок метода, устойчивость, оценка погрешности решения).

Для производных схем, содержащих как линейные, так и нелинейные реактивные и резистивные элементы, аналитических методов решения ДУ не существует.

Дано: ДУ , , ф-ция - известна.

Решаем численным методом, разбивая временной интервал на подинтервалы1

Существует 2 подхода для определения шага дискретизации.

1)

Процессы во время интервала изменяются с одинаковой скоростью.

2) - функция от времени.

Используется для моделирования процессов, которые можно разбить на области быстрых изменений и области медленных измерений.

 

Решение ДУ осуществляется на основе численного интегрирования уравнения вида:

- искомая функция

Существует большое количество, численных методов, позволяющих определить .

- шаг

1 метод Явный метод Эйлера(метод прямоугольника):

2 метод (метод трапеций)

3 метод (неявный метод Эйлера)

Отличие явного метода численного интегрирования от неявного метода заключается в том, что при явном методе неизвестная величина явно вынесена в левую часть.

Обобщение двух точечных методов будет соотношение:

Из которого рассмотрение 3 метода получается при , , .

Переход от одношагового метода к многошаговым повышает точность решения уравнений. Для m шагового алгоритма можем записать:

явный метод

не-явный метод

Погрешность решения ДУ при равномерном шаге зависит от следующих факторов:

1) от величины шага: , чем больше шаг, тем больше будет погрешность

2) от порядка метода: чем выше порядок метода, тем меньше погрешность, , где к – порядок метода, B – зависимость от , 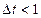Наличие особой точки обусловлено процессами потери устойчивости

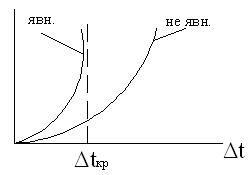
Неявные методы в отличие от явных обладает устойчивостью алгоритма: при увеличении шага погрешность растёт, но потери устойчивости не происходит. В этом преимущество явных методов, а недостаток, более сложная процедура расчета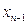

Физически соответствует временному шагу, выбранному с учётом: периода входных сигналов и периода выходных сигналов

12. Формирование линейной модели цепи в частотной области по исходной модели в пространстве состояний.

Исходная модель в пространстве состояний описывается системой уравнений вида:

- вектор состояний, вектор напряжений на ёмкостях и токов в индуктивностях. Его размерность равна числу реактивных элементов в схеме.

- матричные коэффиценты; структура матриц определяется числом реактивных элементов.

Элементы матриц – действительные числа, их величина определяется структурой схемы.

- вектор входных сигналов (вектор независимых источников).

Источники тока и напряжения – входные сигналы. Размерность вектора определяется количеством входных источников.

Данная модель схемы содержит нелинейные элементы, то происходит линеализация их характеристик. Перейдём из временной области в частотную для уравнения состояний и уравнения выхода: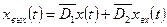

Уравнение выхода, где - выходной ток или выходное напряжение, 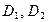- матричные коэффиценты. Переход от времени функций к операторному способу: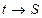

 

Получим: и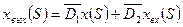

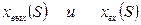- отображение выхода и входа соответственно.

 

При решении задачи анализа известно:

1) изображение входного сигнала

2) параметры схемы

Неизвестно:

1)

2) вектор изображений

 

Выразим из первого уравнения и подставим его во второе уравнение. Получим связь входного, выходного изображения: x – вектор; S – оператор.

 

Нужно ввести единичную матрицу:

; - единичная матрица;

Передаточная функция по определению:

На основе передаточной характеристики могут быть построены АЧХ и ФЧХ как в линейном, так и в логарифмическом масштабе.

В Micro CAP5 переход от линейного к логарифмическому масштабу осуществляется выбором масштаба для x и y. Если пределы изменения частоты не включают ноль, то можно перейти к логарифмическому масштабу. Изменение масштаба по вертикали от линейного к логарифмическому может происходить как с помощью пиктограммы, так и за счёт выбора отображения характеристики в учебнике Богдановича. Аналогично коэффиценту передачи получается и рассчитывается все характеристики, в частотной области(токи, сопротивления, мощности).

 

Анализ в частотной области возможен в диапазоне температур, при этом для неполупроводниковых элементов необходимо давать температурный коэффицент с соответствующим значением в PSpace и в параметрах анализа задаются минимальная температура, максимальная температура и шаг.

 

Вторая разновидность – статический анализ, при котором задаётся для элементов с разбросом допуск.

 

Режим Степпинга – режим подбора параметров. Выбираем элемент, у которого изменяем параметры. Режим многовариантного анализа(семейство характеристик).

 

13. Модель цепи при анализе на постоянном токе. Формирование на основе модели в пространстве состояний.

Анализ на постоянном токе предполагает неизменность входного сигнала во времени. Если на вход подаётся постоянное значение, то и на выходе постоянное значение. Если провести многократный анализ, то геометрически результат анализа – совокупность точек, которые можно соединить линией, зависимостью:

Любые зависимости на постоянном токе – многовариантный анализ. Формирование математической модели схемы на постоянном токе может происходить одним из 2-х способов:

 

1 вариант: удаляем из схемы все реактивные элементы, заменяя индуктивность на короткое замыкание. Вместо L – короткое замыкание, вместо C – холостой ход.

 

В итоге схема будет содержать источники управления и неуправляемые источники тока.

 

Сопротивления линейные и нелинейные.

 

Математически схема будет описываться системой алгебраических (линейных или нелинейных) уравнений. Нелинейность, если присутствуют нелинейные без инерционные элементы. Иногда говорят про системы трансцендентных уравнений.

Эквивалентные алгебраические уравнения используются вместо трансцендентных.

 

2 вариант: берётся исходное уравнение в пространстве состояний

 

 

При этом в статическом режиме все характеристики теряют временную зависимость.

 

, ,

Система ДУ в полных производных вырождается в систему алгебраических уравнений, т.е получаем: II способом приходим к системе алгебраических уравнений: I способом приходим к системе алгебраических уравнений.

 

14. Решение нелинейных уравнений: классификация методов, параметры итерационных методов.

Существует 3 различных класса методов решения нелинейных алгебраических уравнений.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: