 |
Класс: Аналитические методы(корни квадратного уравнения).
|
|
|
|
Известны соотношения для квадратного и кубического уравнения. Математически доказано, что для алгебраического уравнения общего вида с показателем степени 5 и выше, аналитических решений не существует. Поэтому эти методы(аналитические методы) в САПР не используется.
Класс: Графические методы.
Предполагают разбиение уравнения на отдельные функции, построение каждой из этих функций и нахождение точек пересечения графиков. Данный метод мог бы быть эффективным для отделения корней.
Класс: Численные методы.
Существуют десятки методов решения уравнений относящихся и этому классу (детектор, модулятор, сложитель).
Основные характеристики численных методов.
1) Условные сходимости (необходимое и устойчивое условие достижения с заданной степенью точности корня управления на основе итерационного метода).
2) Начальные приближения: обязательна лишь для некоторых методов.
3) Трудоёмкость расчёта одной итерации. Оцениваем количество операций на одну итерацию.
4) Скорость сходимости: характеризуется на сколько уменьшается отношение текущего значения от корня. Скорость сходимости можно косвенно оценить по числу итераций, необходимых для нахождения корня с заданной степенью точности.
В основе, решения численных методов лежит метод итераций. Итерационный метод предполагает последовательное(циклическое) решение уравнений вида:
 , где i = 0, 1,2 …
, где i = 0, 1,2 …
Итерационный процесс может быть закончен, если отклонения по аргументу на ближайших итерациях меньше заданной степени точности.
В данном случае обычно накладывается ограничения на функции f(x) или её производную f ‘(x), достаточным условием сходимости является требование |f ‘(x)|<0 в пределах области определения аргумента  .
.
|
|
|
Существует апостериорная оценка окончания итераций. Смысл данной оценки.
 |
f(x)







X




Существует целый ряд методов, базирующихся на итерационных способах получения решения.
Группы методов:
I. Методы деления по полам: метод простой итерации обладает мягкими условиями сходимости, но не высокая скорость сходимости(большое количество итераций-шагов)
Первая группа используется в 2-х случаях:
1) На начальном этапе поиска корней.
2) Методы II группы начинаются расходиться.
II. Методы с жесткими условиями сходимости, относительно высокая скорость сходимости.
· Метод Ньютона
· Квазиньютоновские методы
· Метод Ньютона – Раввина
· Метод Бройдена
15. Решение нелинейных уравнений: метод половинного деления. Пример.
Условие сходимости:
a) Корень уравнения отделён (есть корень и является единственным).
b) Функция определена на интервале изменения и непрерывна.
Геометрическая интерпретация метода.
 Y
Y


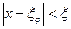



 a
a 


 0 X
0 X
Алгоритм решения:
1) Проверяем:  -условие не выполняется. Если выполняется – корень любой из интервала.
-условие не выполняется. Если выполняется – корень любой из интервала.
2) Находится среднее значение:  и определяем знаки функций в точках
и определяем знаки функций в точках 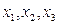 .
.
 , то
, то  , условия не выполняются.
, условия не выполняются.
Можно априорно оценить количество итераций  , где n-количество итераций
, где n-количество итераций  - точность
- точность
При программировании алгоритма необходимо предусмотреть возможность попадания 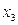 в
в  .
.
 , то
, то  .
.
 , то
, то 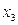 -корень.
-корень.
16. Решение нелинейных уравнений: метод хорд. Пример
Один из наиболее применяемых методов.
17. Решение нелинейных уравнений: метод касательных. Пример
Условия сходимости метода:
1) Функция f(x)-ограничена непрерывна на интервале [a;b].
2) Корень уравнения отделён(единственный корень) => 
3) Существуют производная  на интервале [a;b] и её знак постоянен sing
на интервале [a;b] и её знак постоянен sing  на [a;b].
на [a;b].
|
|
|
4)  -существует,
-существует,  на [a;b] знак 2ой производной постоянен.
на [a;b] знак 2ой производной постоянен.
3 и 4 условия дополнительные требования.
Геометрическая интерпретация метода.
 |
y a) Выбираем начальное приближение.
б) Проводим касательную функцию  в точке
в точке  к функции f(x) до пересечения с осью OX.
к функции f(x) до пересечения с осью OX.
f(x) в) Восстанавливаем перпендикуляр из точки перпендикуляр с осью OX до  , получим новую точу и т.д.
, получим новую точу и т.д.

0 a  b x
b x
Замечание:
Условие сходимости предъявлены к интервалу [a;b], поэтому необходимо оставаться в пределах данного интервала.
Можно так выбрать начальные приближения, что произойдёт выход из интервала [a;b].
Если мы зайдём за пределы интервала, то если выбираем в качестве приближения начальную точку a, то может произойти выход за пределы интервала.
Чтобы остаться в пределах интервалах предъявляются требования к начальным приближениям:
1) Выбирается точка на концах интервала: либо a, либо b.
2) 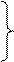 Посмотреть знак
Посмотреть знак 

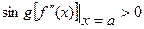 в итоге <0
в итоге <0

 в итоге >0
в итоге >0
 |
y Из прямоугольного треугольника, образованного 1ой касательной


 ,
, 

0 a  b x
b x


 - итерационное соотношение.
- итерационное соотношение.
Итерационное соотношение требует расчёта производной. Обычно производную определяют численные методы. Аналитически можно уменьшить затраты на одну итерацию, если воспользоваться квазиньютоновским методом, предполагающим вычисление производной и использование. Это значение производной используем несколько раз.
Геометрическая интерпретация квази-ньютоновского метода.
 y Использовать более 3х раз одну касательную не целесообразно т.к. начинается существенно увеличиваться количество итераций.
y Использовать более 3х раз одну касательную не целесообразно т.к. начинается существенно увеличиваться количество итераций.

0 a b x
Параллельные линии.
Завершение итерационного процесса: наиболее эффективной метод по изменению знака функции при добавлении  к аргументу
к аргументу  , где
, где  заданная степень точности.
заданная степень точности.
Метод Ньютона один их основных методов решения линейных уравнений.
Преимущества:
1) Высокая скорость сходимости (не вязно уменьшается пропорционально квадрату).
2) Малое число итераций.
Недостатки:
1) Высокая трудоёмкость расчёта одной итерации.
2) Жёсткие условия сходимости.
18. Решение нелинейных уравнений: метод простых итераций. Пример
Есть функция f(x), необходимо найти точку пересечения f(x) с осью OX или найти корни уравнения  . При k-ая уравнение превращается в тождество с заданной точностью
. При k-ая уравнение превращается в тождество с заданной точностью  .
.
|
|
|
От исходного уравнения f(x)=0 перейдем на основе эквивалентных преобразований заданного уравнения к уравнению вида: 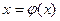 . Если построить итерационную процедуру
. Если построить итерационную процедуру  , то возможны варианты:
, то возможны варианты:
a) Итерационный процесс будет расходиться.
b) Итерационный процесс сходится.
c) Процесс есть расходящийся и сходящийся, или стационарный.
Условие сходимости процесса функция  -определяется на интервале [a;b] и непрерывна.
-определяется на интервале [a;b] и непрерывна.
Существуют произведения  на этом интервале и её значения
на этом интервале и её значения  .
.
Существует целый ряд методов(алгоритмов) формирования функции  . Один из простейших, когда строится соотношение
. Один из простейших, когда строится соотношение  , тогда II условия сходимости может быть представлено в следующем виде
, тогда II условия сходимости может быть представлено в следующем виде 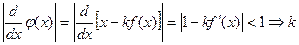 .
.
Из соотношения следует однозначные требования к коэффициенту k. Знаем область определения [a;b] знаем функцию, известна её производная.
Геометрическая интерпретация метода.
 Y
Y


 y = x
y = x
коридор
 |




0 a b X

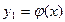
 |





 Угловая спираль Архимеда
Угловая спираль Архимеда
 |


 X
X
 |
 получим квадрат
получим квадрат
Линейная скорость сходимость(привязка уменьшается по линейному закону) не требуется расчёта производных.
19. Статистический анализ: метод малых отклонений. Назначение.
Является математическим обоснованием для группы статических методов,
К этим методам относится:
1) метод моментов
2) метод расчёта на наихудший случай в методе на основе метода малых отклонений(см. Калабеков).
Замечание.
Не путать с расчётом на наихудший случай в методе Монте-Карло. В основу метода малых отклонений положено соотношение: Y=FX
Y – вектор выходных функций:  Вектор
Вектор 
n – количество выходных характеристик
F – оператор, в общем случае нелинейностей
m – количество внутренних параметров
 : n – может быть меньше, больше или равно m (
: n – может быть меньше, больше или равно m ( и
и  ).
).
В частном случае исходное соотношение может быть представлено в виде:

Разложим выходную характеристику в ряд Тейлора относительно номинальных значений параметров.
|
|
|
Получим:

В соотношении не учтены все производные, начиная со 2 порядка и выше.
Если схему отнести к классу 1)б), то 
Для 1)б) 
Данное соотношение устанавливает линейную функциональную зависимость между отклонениями внутренних параметров и отклонением выходными характеристиками.
Частный случай, когда отклонение одной характеристики вызывает отклонение одного параметра.
 , где
, где 

Данное соотношение остаётся справедливым при любых отклонениях внутреннего параметра 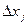 меньших по величине, чем величина, полученная при разложении в ряд Тейлора
меньших по величине, чем величина, полученная при разложении в ряд Тейлора
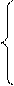

20. Статистический анализ: расчет на наихудший случай. Пример
Условие применимости метода базируется на методе малых отклонений.
Постановка задач Известно:
а) 
б) отклонение внутренних параметров

в) F
 - вектор номинальных значений внутренних параметров
- вектор номинальных значений внутренних параметров
 - номинальное значение j-го внутренних параметров
- номинальное значение j-го внутренних параметров
 - вектор предельного отклонения внутренних параметров(допуск)
- вектор предельного отклонения внутренних параметров(допуск)
F – оператор, устанавливающий связь между векторами выходных функций и внутренними параметрами
Нам требуется определить вектор выходных параметров, соответствующих наихудшему случаю

 - i-ый выходной параметр исключение благоприятных с точки зрения выполнения технического задания
- i-ый выходной параметр исключение благоприятных с точки зрения выполнения технического задания 
Алгоритм Расчёта
Допустим, что условие, работоспособности в техническом задании задано в виде:
1) 
Пример: уровень побочных гармоник или описание характеристики от заданного вида, тогда:

 - максимальное значение i-го выходного параметра
- максимальное значение i-го выходного параметра
 - значение внутреннего параметра, соответствующему случаю и определённому по следующему соотношению:
- значение внутреннего параметра, соответствующему случаю и определённому по следующему соотношению:


2) 
Пример: уровень напряжения, уровень мощности
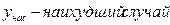



При рассмотренных соотношений должны выноситься условия:
1)  ; sign - знак
; sign - знак
2) 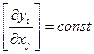
Оба эти условия выполняются на основе малых отклонений
|
|
|


