Алгоритм расчёта по методу Монте-Карло

Преимущества:

а) возможность расчёта сложных схем с большим количеством корреляционных связей и без ограничений на вид зависимости выходной характеристики от внутренних параметров

б) высокая статическая достоверность результатов при правильном выборе количества испытаний

Недостатки:

а) необходимо знать статические сведения о внутренних параметрах в большем объёме по сравнению с другими методами

б) значительные вычислительные затраты порядка 5-10% требуют N порядка 500-1000 испытаний

Данный метод может быть реализован лишь на основе вычислительной техники. При статических испытаниях обычно решаются две задачи:

1.Прямая – по заданным отклонениям внутренних параметров определяется отклонения выходных характеристик 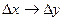Данная задача решается достоверно с помощью нескольких операций (для проверки результатов).

2. Обратная – представляет практический интерес. В общем случае для большого количества элементов порядка 1000, данная задача решений не имеет(трудоёмкая)

Для ряда частных случаев, разработаны алгоритмы решения:

Пример: количество внутренних параметров, имеющих разброс менее 10:

а) для элементов задаём максимальный допуск

б) рассчитываем , соответствует

- определяем достоверность результата

- сравниваем

Если отклонение выходной характеристики не соответствует ТЗ(), то

1. Определяем вляние внутренних параметров на выходную характеристику (Переходим в режим Stepping)

- i-ый внутренний параметр

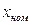- номинальное значение

- допуск

Определяем и ;

k – число интервалов <100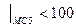

В результате многовариантного анализа получаем семейство выходных характеристик по истинным определяем отклонение :

Итак, для каждого внутреннего параметра сопоставляя значения определяем внутренние параметры влияния которых на обходную характеристику наиболее. У этих параметров уменьшаем величину допуска и переходим к шагу 2. Процедуру завершаем, когда будет удовлетворять требованиям ТЗ.

23. Редактор схем системы Micro-CAP: ограничения, возможности.

24. Моделирование во временной области в системе Micro-CAP. Решаемые задачи.

25. Моделирование в частотной области в системе Micro-CAP. Решаемые задачи.

26. Моделирование на постоянном токе в системе Micro-CAP. Решаемые задачи.

27. Статистическое моделирование в системе Micro-CAP. Решаемые задачи.

28. Многовариантный анализ в системе Micro-CAP: решаемые задачи, ограничения и возможности.

29. Модели сигналов при логическом моделировании.

Моделирование цифровых схем базируется на Булевой алгебре,

Логическая единица – истина, логический ноль – ложь.

Существует положительная потенциальная логика, в основном применяемая:

0, ноль – низкий уровень

1, единица – высокий

Существует отрицательная потенциальная логика: 1- низкий потенциал; 0 – высокий

 

Модели сигналов могут быть классифицированы по количеству кодов:

а) двоичное или двухзначное моделирование 1,0

б) трёхзначное моделирование 1,0,Z

Z – неопределённое состояние, включающее в себя переход из 0в1, 1в 0 и др.

в) пятизначное моделирование 1,0, Z, h,

h – переход 0 в 1; - переход 1 в 0; Z – неопределённое состояние.

 

Замечание: Z в трёхзначном моделировании включает в себя Z шестизначное моделирование, h, Встречаются семи-девяти и более значные представления сигналов, где в качестве состояния выделяются:

- динамический риск сбоя

- статический риск сбоя

- критические состояния

30. Модели элементов при логическом моделировании.

Существует 3 вида базовых логических элементов, реализующих Булевую операцию:

1) логическое И;

2) логическое ИЛИ;

3) инверсия отрицание

Остальные элементы строятся на основе данных элементов.

 

Результат сложения истина(1) – или первый или второй элемент или оба элемента равны 1. Выходные значения сигнала определяются на основе таблицы истинности, устанавливающее соотношение между входными значениями и выходными.

 

Логический элемент – компонент цифрового устройства выполняемых одну или несколько простейших логических операций:

 

Запоминающий элемент – компонента цифрового устройства, оьладающая способностью сохранять своё состояние при отсутствии сигнала на входе – триггер.

Различают 2 типа цифровых устройств:

 

1. Комбинационный – однотактные

Цифровые устройства, в которых значения выходных символов определяются заданной в данный момент времени сочетаний входных воздействий, в комбинационных отсутствует память, чисто логические элементы.

 

2. Последовательные – многотактные – конечные автоматические устройства, в которых выходные сигналы зависят от входных воздействий в заданный момент времени t, но и от их предыдущих значений.

 

31. Методы логического моделирования: классификация, задачи моделирования.

Существует несколько отличающихся методов:

1)решаемыми задачами;

2)исходными данными;

3)трудоёмкостью моделирования.

Методы классифицируются:

1) по признаку учёта задержек элементов в схеме, если задержки не учитываются, то метод синхронный, если учитывается, то асинхронный;

2) по виду модели сигнала (2-х значное моделирование, 3-х, 5-ти значное моделирование);

3) по последовательности решаемых логических уравнений.

1. Метод сквозной (проход последовательностью с входа на выход, не пропуская ни одного уравнения);

2. Событийное моделирование (решаются лишь те уравнения, для которых изменялись значения аргументов, если входные сигналы не изменены – уравнения не решаются).

Первый метод моделирования:

Синхронное логическое моделирование является:

- синхронным;

- двухзначным;

- сквозным.

Оно не учитывает:

- задержки;

- неопределённые состояния;

- состояние перехода из 0 в 1.

Решаемые задачи: проверка правильности логического функционирования схемы без учёта задержки. Если правильно, то провести моделирование с учётом задержки

,

i – количество логических элементов;

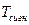- период синхроимпульса.

2 фрагмент: если отрицательный ответ, то нужно исправить схему, синхронное моделирование имеет два варианта реализации:

1 вариант: в схеме отсутствует обратная связь;

2 вариант: с наличием обратной связи.

32. Синхронное логическое моделирование. Пример.

Пример: провести моделирование в схеме.

1 шаг: производим ранжирование сигналов в схеме для обеспечения причинно-следственных связей, при решении логических уравнений. Это нужно, чтобы определить последовательность решения логических уравнений.

х8

х1

		&
			“+” синхронного моделирования: а) наименьшая трудоёмкость расчёта (не используются исходные данные); б) не требуется знания времени задержки. “-” синхронного моделирования: а) решается лишь одна задача. Данный метод исторически – наиболее ранний.
	&
		х5

 

х2

 

 

 

х7

&

х3

	х6

 

 

r = 0

r = 3

r = 2

r = 1

х4

 

 

В данном случае все сигналы разбиваются на ранги (0, 1, 2, 3)

r = 0 – включает входные сигналы (х1, х2, х3, х4);

r = 1 – ; ; ;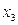

r = 2 – ; ;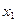

r = 3 – .

На основе логических уравнений составим таблицу истинности:

х1	х2	х2	х4	х5	х6	х7	х8

1) Если результаты сравнения соответствуют ТЗ, то анализируем влияние задержки в устройстве: - устройство работоспособно, - не удовлетворяет условию. Вывод: устройство правильно функционирует.

2) Результаты моделирования ТЗ не совпадают. Редактируем схему, затем повторно проводим синхронный анализ.

Особые случаи синхронного моделирования схемы, содержащей обратную связь (Ильин):

х4

&

r = 2

r = 3

х1

				х6
					х7

 

х2

 

&

х5

r = 0

х3

r = 1

х4

 

Блок задержки в исходной схеме отсутствует; вводится дополнительно при реализации алгоритма расчёта.

Алгоритм расчёта:

1) временно разрываем обратную связь до момента появления в ней сигнала с выхода. Функционально это достигается введением блока задержки;

2) считаем, что на вход элемента с обратной связью поступает заданный нами сигнал (либо 0, либо 1). Аналог начальных условий при расчёте переходных процессов в цепи;

3) ранжируем сигналы, при этом цепи обратной связи присваиваем нулевой ранг;

4) записываем в соответствии с рангами состояния сигналов и логические уравнения.

r = 0: х4, х1, х3, х6;

r = 1: ; ;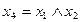

r = 2: ;

r = 3: .

5) задаём входные сигналы и рассчитываем промежуточные значения и выходные величины

|вход |выход

х1	х2	Х3	х4	х5	х6	х7	х8

 

33. Асинхронное логическое моделирование. Основные понятия. Решаемые задачи. Алгоритмы.

Свойства метода:

1) учитывает влияние задержек;

2) используем двухзначное моделирование.

Замечание: асинхронное моделирование для ряда алгоритмов может быть реализовано как трёхзначное;

3) рассмотрение алгоритмов является сквозным.

Задачи, решаемые методом асинхронного моделирования:

а) правильность логического функционирования схемы с учётом времени задержки;

б) выявление статистических рисков сбоя;

в) выявление динамических рисков сбоя;

Идея метода: при синхронном моделировании анализ происходит в моменты изменения входных сигналов. Так как элементы считаются при синхронном моделировании без инерционным, то изменение выходного сигнала происходит в те же самые моменты времени.

Асинхронное моделирование:

 

 

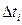
- без инерционная логическая функция

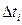- время задержки выходного сигнала при асинхронном моделировании.

Замечание: если задержка есть хотя бы в одном элементе, то моделирование асинхронное.

При асинхронном моделировании необходимо анализировать сигналы: решать логические уравнения. В моменты времени 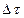, где - наибольший общий делитель всех времён задержки и периода синхроимпульса.

Пример:

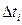= {3,9,12,27}

= 150

Наибольший общий делитель (НОД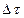) = 3 → = 3

Если число будет дробное, то

1) переходим в область целых чисел;

2) числа, меньшего единицы, не будет.

Выбор интервала 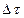= 3 обеспечивает выявление изменения сигнала в момент его появления.

В данном примере трудоёмкость асинхронного моделирования в 50 раз оказывается выше, чем синхронного.

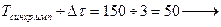асинхронное моделирование всегда более труднее, чем синхронное.

Замечание: увеличение 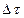по сравнению с рассчитанным приводит к появлению погрешности в анализе.

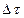, = 4, тогда на интервале [ 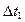, 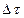] – полный сигнал.

Если 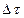↓, то неизвестно …!

 

Риски сбоя – появление на выходе ложного сигнала. Существует 2 вида рисков сбоя:

1) Статистический риск сбоя – называется появление ложного сигнала на выходе при неизменном выходном сигнале (статистическом сигнале) Истинный сигнал статичен (постоянен). при срабатывании логических элементов; время передачи по каналу.

2) Динамический риск сбоя – появление на выходе ложного сигнала при условии, что истинное значение сигнала на выходе изменяется, т.е. необходимым условием появления динамического риска сбоя в элементе – подача на его вход статистического риска сбоя (нужно 2 элемента для динамики).

 

Критические состязания появляются в логических схемах с обратными связями (ОС). Характеризуется устойчивым состоянием, зависящим от значения задержек в элементах.

Устойчивые состояния определяет очерёдность переключения элементов памяти.

Для определения критического состязания необходимо убедится:

1) что есть ОС;

2) провести анализ схемы с заданными значениями задержек;

3) изменить величину задержек и вновь произвести анализ.

Замечание: количество повторяемых алгоритмов выбирается в зависимости от соотношения задержек.

 

Нужно произвести перестановки (менять задержки). Обычно процедура перестановок осуществляется автоматически алгоритмом анализа.

Если получаются различные значения, то критические состязания наблюдаются.

“+” – асинхронное моделирование позволяет решать новые задачи по сравнению с синхронным моделированием риска сбоя критические состязания и работоспособность с учётом времени задержки.

“-”: процедура более трудоёмкая, во много раз по сравнению с синхронным методом моделирования;

1) необходима дополнительная информация по сравнению с синхронным во временах задержки.

34. Асинхронное событийное моделирование. Основные понятия. Решаемые задачи.

Свойства:

1) метод двухзначного моделирования (0 или 1);

2) с учётом задержки;

3) в рабочем цикле не проводится моделирование, но однократно сквозное моделирование в этом методе проводится.

Идея: для больших схем обычно изменения входных сигналов (активное состояние) наблюдается для малого количества логических элементов.

 

Логические элементы динамика

Логические элементы стационарные

 

>> => выгоднее использовать

событийное моделирование.

Нужно решать лишь те логические уравнения, которые описывают логические элементы с изменёнными входными сигналами.

 

 

Вход ЛЭ Выход

Вход = const=> Выход = const

Информация о состоянии выходных сигналов находится в массиве состояний. Данный массив содержит все входные сигналы для логических элементов. Получают эти значения на основе однократного асинхронного моделирования. Асинхронное моделирование осуществляется сквозным методом. Формируется очередь будущих событий, которая содержит указание на то какие элементы (логические уравнения) необходимо решать, если изменились значения в массиве состояний. Очередь будущих событий отображает причинно-следственные связи. Выбор временного шага при событийном моделировании и при сквозном моделировании аналогичен, однако, при событийном моделировании количество анализируемых , , где , , при событийном моделировании.

Плюсы данного метода:

1) эффективный метод для схем с большим количеством элементов (сотни и выше) и большое число наборов входных сигналов. Многовариантный анализ относительно входного сигнала.

Минусы:

1) требуется однократное моделирование на основе сквозного алгоритма;

2) условие алгоритма за счёт формирования и работы с массивами состояний и очередью будущих состояний.

 

 

35. Многозначное моделирование цифровых схем. Решаемые задачи. Алгоритмы.

 

Свойства:

1) трёхзначное моделирование, либо пятизначное моделирование;

2) по алгоритму многозначное моделирование относится к синхронному методу;

3) сквозной алгоритм расчёта.

 

Трёхзначное моделирование решает задачи:

а) правильность логического функционирования схемы;

б) возможность появления статического риска сбоя.

 

Замечание: необходимые условия, но не достаточные.

Необходимое условие превращается в достаточное, если реализована задержка одного сигнала относительно другого.

Необходимые условия появления динамического риска сбоя (статический риск сбоя на выходе логического элементы).

 

Определение критических состязаний:

Рассмотрим необходимые условия их появления, которые заключаются в том, что в схемах с ОС, в ОС возникают неопределённые состояния (см. Ильин).

 

Идея: рисуем схему. Есть ОС, то анализируется.

см. самостоятельно Ильин.

1) схема без ОС (1 набор, 2-ой набор)

 

Пятизначное моделирование

 

Решаемые задачи:

1) правильность логического функционирования;

2) определение статического риска сбоя;

3) определение динамического риска сбоя;

4) определение критических состязаний;

5) переход из “0”в “1”;

6) переход из “1”в “0”;

Особенности моделирования такие не как у трёхзначных: увеличивается количество входных сигналов.

См. Ильин.

“+”: по сравнению с синхронным моделированием решаются новые задачи, но по сравнению с асинхронным моделированием менее трудоёмким для большинства схем.

“-”: по сравнению с асинхронным определим необходимые условия; по сравнению с синхронным моделированием выше трудоемкость..

 

Оптимизация.

“Машинные методы анализа и проектирования электронных схем”.

Оптимизация завершит этап проектирования, при котором определяется совокупность внутренних параметров схемы (значения ёмкостей, сопротивлений, источников сигнала и т.д.), обеспечивающих необходимые значения выходных характеристик (быстродействующее время задержки сигнала, потребляемая мощность, уровень сигнала на выходе).

Y= F*X, где

X– вектор внутренних параметров

Y– вектор выходных характеристик

Известна целевая функция, которая является Yоптимальной.

Обычно целевая функция в пакете формируется на основе одной характеристики.

Существуют аналитические методы расчёта оптимальных параметров, реализуются лишь для частных случаев:

1) гладкая функция одного аргумента;

2) существуют численные методы расчёта.

Численные методы расчёта используют в пакетах схематического проектирования.

Алгоритмы численных методов являются итерационными, определяются коэффициентами чувствительности для изменения параметров, учитываются предыдущие шаги.

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: