 |
Для описания основных свойств статистических распределений чаще всего используют выборочные характеристики следующих видов: 1) средние; 2) характеристики вариации (рассеяния).
|
|
|
|
Графическое изображение рядов распределения:полигоны и гистограммы частостей(частот).Графическое изображение накопленных частот и частостей(кумуляты).
Для наглядности принято использовать следующие формы графического представления статистических распределений: полигоны и гистограммы. Дискретный ряд изображают в виде полигона. Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами (x i, m i); аналогично полигон относительных частот - ломаная, отрезки которой соединяют точки с координатами (xi, wi ).
Интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых - интервалы длиной hi, а высоты - плотности частот mi/hi. Для гистограммы относительных частот высоты прямоугольников - плотности относительных частот 
. Здесь в общем случае 
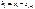, однако на практике чаще всего полагают величину h одинаковой для всех интервалов. 
где i =1, 2,..., k.
Площадь гистограммы есть сумма площадей ее прямоугольников.
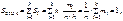
таким образом, площадь гистограммы частот Sч равна объему выборки, а площадь гистограммы относительных частот Sотн.ч равна единице.
В теории вероятностей гистограмме относительных частот соответствует график плотности распределения вероятности 
.
Кумулятивные ряды графически изображают в виде кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат - накопленные частоты Н (x) или относительные накопленные частоты F*(x), а затем точки с координатами (x i; H (x i)) или (x i; F*(xi)) соединяют отрезками прямой. В теории вероятностей кумуляте соответствует график интегральной функции распределения F(x).
|
|
|
Характеристики рядов распределения: выборочная средняя арифметическая. мода. медиана, выборочная диперсия, выборочное среднее квадратическое отклонение, коэффициент вариации, размах вариации.
Для описания основных свойств статистических распределений чаще всего используют выборочные характеристики следующих видов: 1) средние; 2) характеристики вариации (рассеяния).
Существуют различные виды средних: средняя арифметическая, средняя геометрическая и др. Это так называемые аналитические средние. Основным видом аналитических средних является средняя арифметическая, или выборочная средняя. Выборочная средняя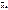 
характеризует типичное для выборки значение признака Х. Она также приближенно характеризует (оценивает) типичное для генеральной совокупности значение признака Х. Если данные наблюдения не сгруппированы, то выборочная средняя 
рассчитывается как простая средняя арифметическая:
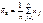.Если же данные сгруппированы, то выборочная средняя 
рассчитывается как взвешенная средняя по одной из следующих формул:
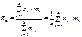
Здесь частоты mi и частости wi являются весами.Следует отметить, что данные формулы непосредственно применимы только к статистическому распределению дискретного приз(дискретному ряду).
Для статистических распределений используют еще структурные, или порядковые, средние. Из них наиболее часто применяют медиану и моду.
Медиана хме -это серединное значение признака Х, то есть значение признака, которое делит ранжированный вариационный ряд на две равные по численности группы. Медиана х ме определяется следующим образом:
, если n = 2 j - четное; х ме = хj+ 1 , если n = 2 j +1 - нечетное.
Из определения накопленной относительной частоты следует, что
. Мода 
- наиболее часто встречающееся значение признака X, то есть такое значение признака X в выборке, которому соответствует наибольшая частота. Следовательно, х мo = xi , если mi = m max .
|
|
|
Самую грубую оценку рассеяния значений признака дает размах вариации R = х max- х min, который учитывает лишь два крайних значения признака. Но он не дает представления о расположении вариант вокруг средней.
Для оценки колеблемости значений признака относительно средней чаще всего используют дисперсию.
Выборочная дисперсия DB есть выборочная средняя арифметическая квадратов отклонений значений признака X от выборочной средней 
, то есть
.
Если данные наблюдения не сгруппированы, то выборочная дисперсия определяется следующей формулой:
.
Для сгруппированных данных находят выборочную взвешенную дисперсию:
и 
.
Эти формулы непосредственно применимы только к статистическому распределению дискретного признака (дискретному ряду).
Выборочную дисперсию еще можно определить по формуле
,
то есть выборочная дисперсия равна среднему квадрату без квадрата средней.
Средний квадрат есть выборочная средняя арифметическая квадратов значений признака X (данные наблюдения не сгруппированы и сгруппированы, соответственно):
и 
.
Однако дисперсия вследствие суммирования квадратов отклонений дает искаженное представление о самой величине отклонений, измеряя их в квадратных единицах. Поэтому, используя дисперсию, вводят еще характеристики: выборочное среднее квадратическое отклонение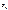 
и коэффициент вариации 
.
Выборочное среднее квадратическое отклонение (
) есть арифметическое значение корня квадратного из выборочной дисперсии, т.е.
.
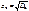Оно показывает, на сколько в среднем отклоняются значения xj признака X от выборочной средней 
. Измеряется 
в тех же единицах, что и сам признак. Величина является наиболее удобной и чаще всего применяемой характеристикой рассеяния.
Коэффициент вариации 
равен процентному отношению среднего квадратического отклонения к средней, то есть 
. Он показывает, сколько процентов от выборочной средней составляет среднее квадратическое отклонение. Коэффициент вариации характеризует однородность совокупности значений признака. На практике считают, что если 
, то совокупность считается однородной, в противном случае - неоднородной.
3.3.Параметры генеральной совокупности.Статистические оценки параметров генеральной совокупности:точечные и интервальные.
|
|
|
Важной задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака X генеральной совокупности. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения. При решении задачи статистического оценивания параметров распределения необходимо учитывать вероятность, характеризующую степень достоверности принимаемого решения. Статистические оценки могут быть точечными и интервальными.
Пусть имеется генеральная совокупность объема N, элементы которой обладают признаком Х. Допустим, что все значения признака Х не сгруппированы. Тогда генеральная средняя признака Х будет равна
Если рассматривать признак Х как случайную величину, то он будет иметь следующее распределение:
| xj | х1 | х2 | ... | хN |
| pj | 1/N | 1/N | ... | 1/N |
так как вероятность взять наудачу один элемент хi из генеральной совокупности равна 1/N. Найдем математическое ожидание признака Х:
,
то есть 
.
Это же можно получить и в случае, если значения признака Х сгруппированы. Получим ряд распределения, например, частостей:
| xi | x1 | х2 | ... | хk |
| pi | m1/N | m2/N | ... | mk/N |
Тогда
.
Аналогично
.
.
Таким образом, генеральные характеристики признака Х по своей сути и численно совпадают с характеристиками случайной величины.
Эти характеристики назовем параметрами генеральной совокупности признака Х или параметрами теоретического распределения. Как правило, эти параметры неизвестны. Однако их можно оценить (приближенно определить). В результате оценивания получают статистические оценки неизвестных параметров распределения.
|
|
|
