Доверительный интервал для генеральной доли

N,M-обладают свойством А, N-объем генеральной совокупности

р_ген=М/N=P(A)-генеральная доля

Извлекаем n элементов, т.е. сделаем выборку n<<N и найдем по этой выборке выборочную долю

р_выб=m/n, р_{выб –} случайная величина, по теореме Ляпунова р_{выб ~} НЗР(р_ген; р_{ген *} q_ген/n)

Зададим ɣ?(0,1) следовательно Δ>0

P(׀ р_{выб –} р_ген ׀< Δ)= ɣ, т.к. р_ген =М(р_выб), следовательно P(׀ р_{выб –} М(р_выб) ׀< Δ)= ɣ

2Ф(Δ/G(р_выб))= ɣ, G(р_выб)≈ 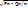, Ф(t)= ɣ/2, Δ=t*G(р_выб)=t*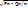

 

Состояние гип Н0	Результаты проверки
принимается	отвергается
верна	верное решение	Ошибка 1 рода
неверна	ошибка 2 рода	верное решение

4.1. Статистические гипотезы - это любое предположение о виде распределения или параметрах распределения генеральной совокупности. Любую гипот. проверяют на соответствие данным выборки. В стат. сначала выдвигиются основные гип. H₀. Нулевая гипотеза явл. наиболее правдоподобным предположением о ген. совок., которое до проверки его до выборки априори явл. верным. Конкурирующ. гип. H₁. Гипотезу H₀ проверяют с помощью спец. построенной случайной величины. Гип. H₀ проверяют с помощью спец. постороенной СВ. К-спец. постороенное СВ. Все множество значений СВК разбив. на 2 непересекающихся подмножества. 1.W – крит. область или область неправдоподобных значений критерия. 2. W – область допустимых значений К.3. К принадлежит WU W. Если К набл. принадл W, то считают, что данные наблюд не согласуются с гип. Н₀. Если же Кнабл. принадл W счит, что данные наблюд согласуются с гип Н₀, и она не отвергается.
Ошибки 1–го и 2–го рода. Ошибка 1 рода заключается в том, что будет отвергнута справ. гип. Н₀. Вероятность ошибки 1 рода – α. Ошибка 2 рода состоят в том, что будет принята гип. Н₀, в то время когда верна Н₁.α-уровень значимости критерия β-вероятность ошибки 2 рода 1-β вероятность отвергнуть ложную гипотезу Но
Статистическим критерием называется случайная величина, которая используется с целью проверки нулевой гипотезы.
Существуют различные статистические критерии, применяемые на практике: U- и Z -критерии (эти случайные величины имеют нормальное распределение); F -критерий (случайная величина распределена по закону Фишера - Снедекора); t -критерий (по закону Стьюдента); c² -критерий (по закону "хи-квадрат") и др.
Множество всех возможных значений критерия можно разбить на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза принимается, а другое - при которых она отвергается.
Множество значений критерия, при которых нулевая гипотеза отвергается, называется критической областью. Будем обозначать критическую область через W.
Наблюдаемым значением статистического критерия называется значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения.
Множество всех возможных значений выбранного статистического критерия делится на два непересекающихся подмножества. Первое подмножество включает в себя те значения критерия, при которых основная гипотеза отвергается, а второе подмножество – те значения критерия, при которых основная гипотеза принимается.
Критической областью называется множество возможных значений статистического критерия, при которых основная гипотеза отвергается.
Правосторонняя: К>k_{крит. пр}
Левосторонняя: К<k_{крит. л}
Двухсторонняя: К<k_крит.л или К>k_{крит. пр P(|}К|<k крит.дв)=α
Областью принятия гипотезы или областью допустимых значений называется множество возможных значений статистического критерия, при которых основная гипотеза принимается. W
Если наблюдаемое значение статистического критерия, рассчитанное по данным выборочной совокупности, принадлежит критической области, то основная гипотеза отвергается. Если наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то основная гипотеза принимается.
Критическими точками или квантилями называются точки, разграничивающие критическую область и область принятия гипотезы.
Критические области могут быть как односторонними, так и двусторонними.
Уровнем значимости а называется вероятность совершения ошибки первого рода.
Значение уровня значимости а обычно задаётся близким к нулю (например, 0,05; 0,01;0,02 и т. д.), потому что чем меньше значение уровня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Нo.

4.2.1 Гипотеза о нормальном законе распределения генеральной совокупности
Во многих практических задачах точный закон распределения исследуемого признака Х генеральной совокупности неизвестен. В этом случае необходимо проверить гипотезу о предполагаемом законе распределения. Выдвигаются нулевая гипотеза Н0 и ей конкурирующая Н1.
Н0: признак Х имеет нормальный закон распределения.
Н1: признак Х имеет закон распределения, отличный от нормального.
Нулевая гипотеза проверяется с помощью критерия согласия.
Критерий c² (“хи-квадрат”) Пирсона – наиболее часто употребляемый критерий, может применяться для проверки гипотезы о любом законе распределения. Независимо от того, какое распределение имеет Х, распределение случайной величины c² (хи-квадрат): , где – эмпирические частоты, 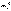– теоретические частоты; при 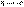стремится к c 2 – распределению с k степенями свободы. k=s-r- 1, где s - число частичных интервалов, r - число параметров предполагаемого распределения, которые оцениваются по данным выборки. В нашем случае предполагают нормальное распределение, значит, оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), отсюда r =2, поэтому k=s- 3.
Проверим гипотезу Н₀ при заданном уровне значимости a.
Теоретические частоты определяются, исходя из предположения о законе распределения генеральной совокупности, в данном случае о нормальном законе. Так как p_i=m_i/n, где рi – теоретическая вероятность, то 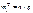. Для непрерывного признака X теоретическая вероятность представляет собой вероятность попадания случайной величины Х в частичный интервал 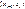. Таким образом, 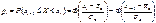,где Ф (t) - функция Лапласа, выборочная средняя 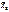и выборочное среднее квадратическое отклонение 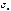- оценки параметров предполагаемого нормального распределения, найденные по выборке объема n.
Можно показать, что для дискретного признака теоретическую вероятность p_i находят следующим образом: ,где 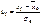; - дифференциальная функция нормированного нормального распределения, шаг - выборочная средняя; - выборочное среднее квадратическое отклонение.
Итак, найдены теоретические частоты данного распределения в предположении, что оно подчиняется нормальному закону.
При проверке нулевой гипотезы о законе распределения генеральной совокупности строится правосторонняя критическая область . Границу раздела областей W и W - точку 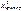находят из условия , где - заданный уровень значимости и k - число степеней свободы.
Если наблюдаемое значение критерия c² _набл попало в область принятия гипотезы (c² _набл <c² _{крит.пр}(a, k), как показано на рис., то нет оснований отвергать нулевую гипотезу, по данным наблюдения признак Х имеет нормальный закон распределения, расхождение между эмпирическими m^э_i и теоретическими m^T_i частотами случайное.
Если наблюдаемое значение критерия c² _набл попало в критическую область (c² _набл > c² _{крит.пр}(a, k), то нулевая гипотеза отвергается, принимается как наиболее правдоподобная конкурирующая гипотеза, то есть признак Х имеет закон распределения, отличный от нормального, расхождение между эмпирическими m^Э_i и теоретическими m^T_i частотами значимо.
чтобы проверить гипотезу о нормальном распределении генеральной совокупности, необходимо:
1) по данным выборки объема n найти теоретические частоты m^T_i;
2) найти наблюдаемое значение критерия c² _набл;
3) из таблицы критических точек распределения c ² (прил. 4) по заданному уровню значимости a и числу степеней свободы k=s- 3 найти c² _крит. (a, k) - границу правосторонней критической области
4) сравнить c² _набл с c² _крит (a, k) и сделать вывод.
Замечание 1. Необходимые условия применения критерия Пирсона:
1) объем выборки должен быть достаточно велик, по крайней мере не менее 50 наблюдений;
2) каждый частичный интервал должен содержать не менее пяти наблюдений. Если это количество в отдельных интервалах мало, то имеет смысл объединить некоторые интервалы, суммируя частоты.
Замечание 2. Очевидно, что при проверке гипотезы о законе распределения контролируется лишь ошибка первого рода.

4.2.2Гипотеза о нормальном законе распределения генеральной совокупности
Пусть даны две генеральные совокупности Х и Y, которые имеют нормальный закон распределения. Есть основание предположить, что их генеральные дисперсии равны, то есть выдвинуть нулевую гипотезу Н ₀: D (Х) = D (Y). Проверим эту гипотезу при заданном уровне значимости a.

Для этого проведем независимые выборки из этих данных генеральных совокупностей с объемами, соответственно, равными n_x и n_y. По данным выборок находим оценки генеральных дисперсий - исправленные выборочные дисперсии S²_x, S²_y, которые будут несмещенными оценками, то есть 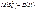и . Тогда нулевую гипотезу можно записать и так: Н ₀: = .

Гипотеза Но проверяется с помощью СВ

Если D(X)=D(Y), то случайная величина F имеет распределение Фишера - Снедекора k₁=n₁-1 и k₂=n₂-1 степенями свободы

Здесь n ₁ - объем выборки, по которой рассчитана , n ₂ - соответственно, .

По выборочным данным находят F_набл. Далее нужно найти критическую точку F _крит и критическую область, которая строится в зависимости от вида конкурирующей гипотезы.

Чаще всего выбирают конкурирующую гипотезу следующего вида:

Н ₁: D (Х) > D (Y).

Эта конкурирующая гипотеза определяет правостороннюю критическую область , которая строится, исходя из требования (F > F _крит (a, k₁, k₂))= a (здесь F _крит (a, k₁, k₂) = F _{крит. пр} (a, k₁, k₂)).

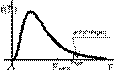
При формулировке вывода руководствуются следующим правилом: если наблюдаемое значение критерия F _набл попало в область принятия гипотезы (F _набл < F _крит(a, k ₁, k ₂)) (рис. 35), то нет оснований отвергать нулевую гипотезу по данным наблюдения D (Х) = D (Y), и расхождение между исправленными выборочными дисперсиями случайное; если же наблюдаемое значение критерия F _набл попало в критическую область (F _набл > F _крит(a, k ₁, k ₂)), то нулевая гипотеза отвергается, а принимается конкурирующая гипотеза D (Х) > D (Y), то есть расхождение между исправленными выборочными дисперсиями значимо.

Замечание. При проверке гипотезы о равенстве генеральных дисперсий при заданном уровне значимости a контролируется лишь ошибка первого рода, но нельзя ничего сказать о степени риска, связанного с принятием неверной гипотезыНо, то есть с возможностью ошибки второго рода.

 

4.2.3

Сравнение дисперсий двух нормально распределенных генеральных совокупностей при неизвестных, но равных дисперсиях.

Пусть СВХ~ N (x ген D(X))
СВУ~ N (y ген), D (Y)).
Параметры: М(Х), D(Х), М(У), D(У) – неизвестны. Однако, известно, что D(Х)=D(У).

Н0: X ген = Y ген, или М(х)=М(У). Всегда можно выдвинуть Н1 в качестве альтернативы. Н1: х ген≠ у ген или М(х)≠М(у). Кроме того вместо Н1 можем выдвин более радикальное предположение. Если х в> y в, то Н1: х ген> y ген или М(х)>М(у). Если же х в.< у в, то как альтернативная гип.

Но можно проверить с помощью СВТ

 

.

Если Н0 верно, то СВТ имеет распределения t (k=nx+ny-2)
При этом предполагают, что СВХ~N(M(X),D(X))
СВУ~N(M(Y),D(Y))

Н0=>СВТ имеет t (k=nx+ny-2). Для того, чтобы проверить ген Н0 проводят 2 выборки: nx=>CBX,ny=>CBY. По выборкам вычисляют несмещенность оценки для М(Х) и D (Х), т.е. хв, Sx2 Далее вычисляют наблюд значение статистики Т подставляя туда оценки. Tнабл – значение. В зависимости от вида альтернативной гип. След. Строить либо одностор либо двусторон критические области.
Н1: М(х)≠М(у), (Уген≠ Хген) (строим двустороннюю) – W: |T|>Tкр.дв. Tкр.дв может быть найдена по заданному a и к=n_x+n_y-2

P_Ho(|T|>Tкр.дв)=a

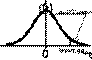
Tкр.дв. на практике находится из спец. Таблицы содержащей Ткр.

Замечание. При проверке гипотезы о равенстве генеральных средних при заданном уровне значимости aконтролируется лишь ошибка первого рода, но нельзя ничего сказать о степени риска, связанного с принятием неверной гипотезы, то есть с возможностью ошибки второго рода.

Если Н₁ :М(Х)<М(У) Хген < Уген строим левостор Т крит.

Схема проверки Но:

Если Т набл Î W, то нет оснований отвергать Но, Но принимает и считаем, что различия между Хв и Ув случайны, незначимы, несущественны, если Ï то принимется Н₁.

Если Н₁ Хген ≠ У ген, различия между Хген и Уген значимо. Существенно

Если Хв больше Ув, то это означает Хв значимо больше, сем Ув

Проверка корректна лишь в том случае, если D(X)=D(Y). Если о дисперсии ничего не известно, то предварительно проверяется Но вспомогат.: D(X)=D(Y). СВ F = S²_{большая}/S²_{меньшая.} Если удалось принять Но вспомог., то далее применяется Т-критерий, в противном случае решение задачи следует прекратить

 

4.2.4 Проверка гипотезы о равенстве вероятности

По отношению к событию А проводят n независимых испытаний с вероятностью p при каждом испытании. Эта вероятность неизвестна, но есть основание предположить, что она равна некоторой величине р0, называемой гипотетической вероятностью. Чтобы проверить это предположение, находят статистическую вероятность m/n она, как правило, отличается от гипотетической вероятности. Выдвигается нулевая гипотеза Н0: р=р0. Конкурирующая гипотеза может быть трех видов: Н1: р>р0(правосторонняя), Н1: р<р0(левостор.), Н1: р≠р0 (двустор). Нулевая гипотеза проверяется по выборочным данным с помощью случайной величины, СВU ~N(0.1) Имеющей в предположении справедливости Н0 нормированное нормальное распределение(q0=1-p0).
По данным наблюдения вычисляется наблюдаемое значение критерия Uнабл. Критическое значение критерия находится с помощью функции Лапласа с учетом вида критической области: - в случае альтернат гип Н1: р>р0 u крит. пр. определяется из условия Ф(u крит.пр.)= 0,5-α; - при Н1: р<р0 u крит. лев. = -u крит. пр., где u крит. пр. находят так же, как и в первом случае; - в случае Н1: р≠р₀uкрит. дв определяется из условия Ф (uкрит. дв) = (1 - α)/2. Далее сравниваются Uнабл. и uкрит. с использованием графиков. При формулировке вывода руководствуются следующим правилом: - если наблюдаемое значение критерия Uнабл. попало в область принятия гипотезы, то нет оснований отвергать нулевую гипотезу, по данным наблюдения р=р0, расхождение между гипотетической вероятностью р0 и статистической вероятностью m/nслучайно; - если наблюдаемое значение критерия Uнабл. попало в критическую область, то нулевая гипотеза отвергается, справедлива конкурирующая гипотеза, расхождения между гипотетической и статистической вероятностями значимо.

Н ₀: р = р ₀ , Н ₁: р > р ₀ .

Гипотезу Н ₀ проверим с помощью случайной величины,

которая имеет нормированное нормальное распределение. Критическая точка находится с помощью функции Лапласа1. Н ₀: р = р ₀; Н ₁: р ≠ р ₀ (критическая область двусторонняя, рис. 44). Строим ее, исходя из требования .
Р(U <- U _{крит.дв})= Р(U>U _{крит.дв})=a/2.

Отсюда следует, что достаточно найти только правостороннюю критическую точку.

Рассмотрим правило нахождения U _{крит.дв}, используя равенство

Р (U>U _{крит.дв})= a/2. ,

(***)

но (по условию), (по определению функции Лапласа).

Тогда равенство (***) примет вид . Отсюда .

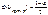По таблице значений функции Лапласа (прил. 2) находим U _{крит дв}.

Затем сравниваем с U _набл и U _{крит дв}. Если | U _набл |< U _крит дв

 

2. Н ₀: р = р ₀; Н ₁: р > р ₀ (критическая область правосторонняя, рис. 42). Она строится из требования 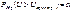при справедливости нулевой гипотезы.

Воспользуемся равенством (***)

или ,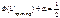

отсюда .

По таблице значений функции Лапласа (прил. 2) находим U _{крит пр} и сравниваем с U _набл. р = р ₀; расхождение между наблюдаемой относительной частотой и гипотетической вероятностью незначимо р > р ₀ Расхождение между относительной частотой и гипотетической вероятностью значимо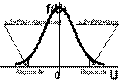

 

Раздел 5. Корреляционно- регрессионный анализ.

Корреляционный анализ – позволяет оценить тесноту линейной взаимосвязи между СВХ и У.

Для того, чтобы оценить тесноту взаимосвязи СВХ и У делают выборку из двумерной ген. совокупности(х,у).

хi	х1	х2	...	хn
yi	y1	y2	...	yn	.

линейная зависимость

Для оценки тесноты лин. взаимосвязи следует найти выборочн. коэф. корреляц. (rв)

, где ху=1/n суммаХiYi

Основные свойства rв: 1. | rв | ≤1, т.е. -1≤ rв ≤1; 2. Чем ближе |rв| к 1, тем теснее линейная связь между Х и У; 3. Если rв = ±1 то можно считать, что у=кх+в, причем r в =1=>k>0, r в = -1 =>k<0; 4. Если r в < 0, то с ростом х в среднем у падает, т.е. связь между х и у отрицательная или обратная. Если r в > 0, то с ростом х в среднем у растет, тогда связь прямая или положительная. 5. r в ≈ 0, то это говорит об отсутствии тесной линейной связи между Х и У, на самом деле близость r в ≈0: а). отсутствия какой-либо взаимосвязи между х и у, б). имеется нелинейная связь между х и у.
Проверка значимости выборочного коэффициента корреляции. В ген. совокупности показателем наличия линейной взаимосвязи явл. теоретический или генеральный коэф. корреляции r в ≈ r ген
r в – СВ, которая меняется от выборки к выборки, оценка r_ген
1). Да, действительно сущ. линейная взаимосвязь между Х и У r в ≠ 0, => r ген ≠0
2). Нет, никакой взаимосвязи нет, r ген = 0. Для того чтобы выбрать ответ выше указанные, нужно решить значимо ли отличие от 0 r в

Н0: r ген = 0, т.е. r в отлич от нуля ≡незначит.
Н1: r ген ≠0, т.е. r в значим.
Если Н0 – верна, то СВТ ~ t(n - 2). 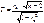По виду гип Н1 строят двустор критич область W: | T |>Tкрит.дв. Если приняли Н1 то можно считать что между СВ Х и У имеется тесная линейная статистическая зависимость. Принятие Но означает что Хи У некоррелированные. Если удалось принять Но следует построить уравнение линейной регрессии

 

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: