 |
Интервальная оценка(доверительный интервал) для математического ожидания нормально распределенной случайной величины при неизвестном среднем квадратическом отклонении.
|
|
|
|
Пусть признак Х генеральной совокупности (случайная величина Х) имеет нормальное распределение, причем среднее квадратическое отклонение  этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание
этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание 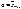 этого распределения. В данном случае при построении интервальной оценки для генеральной средней
этого распределения. В данном случае при построении интервальной оценки для генеральной средней  нельзя использовать закон распределения выборочной средней
нельзя использовать закон распределения выборочной средней  , потому что он зависит от параметра
, потому что он зависит от параметра  , который предполагается неизвестным. Поэтому вместо закона распределения выборочной средней
, который предполагается неизвестным. Поэтому вместо закона распределения выборочной средней  рассмотрим распределение следующей случайной величины:
рассмотрим распределение следующей случайной величины:
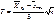 , где S - исправленное выборочное среднее квадратическое отклонение; n - объем выборки.
, где S - исправленное выборочное среднее квадратическое отклонение; n - объем выборки.
Лемма. Пусть признак Х генеральной совокупностиимеет нормальное распределение с параметрами  и
и  ,
,  и
и  - оценки этих параметров, найденные по выборке объема n. Тогда случайная величина
- оценки этих параметров, найденные по выборке объема n. Тогда случайная величина 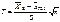 имеет распределение Стьюдента с
имеет распределение Стьюдента с 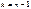 степенями свободы. Доказательство. Очевидно, что распределение случайной величины Т можно представить в виде
степенями свободы. Доказательство. Очевидно, что распределение случайной величины Т можно представить в виде
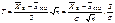 . Рассмотрим случайную величину
. Рассмотрим случайную величину 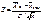 . Эта величина имеет нормальное распределение в силу свойства устойчивости нормального закона (см. п. 5.5.4). Найдем числовые характеристики случайной величины Z:
. Эта величина имеет нормальное распределение в силу свойства устойчивости нормального закона (см. п. 5.5.4). Найдем числовые характеристики случайной величины Z:
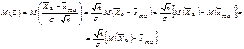
Так как ранее было показано, что 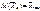 , то
, то 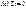 .
.
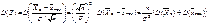 .
.
Так как 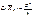 и
и 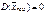 , то
, то  . Следовательно, случайная величина Z имеет нормированный нормальный закон распределения.
. Следовательно, случайная величина Z имеет нормированный нормальный закон распределения.
Рассмотрим теперь случайную величину 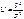 . Так как
. Так как 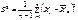 , то распределение величины U можно представить в виде
, то распределение величины U можно представить в виде
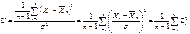 . Полученное выражение для U содержит сумму квадратов n случайных величин
. Полученное выражение для U содержит сумму квадратов n случайных величин  (i =1,2,…,n). Каждая случайная величина
(i =1,2,…,n). Каждая случайная величина 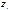 имеет нормальное распределение в силу свойства устойчивости нормального закона. Найдем числовые характеристики
имеет нормальное распределение в силу свойства устойчивости нормального закона. Найдем числовые характеристики 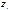 :
:
|
|
|
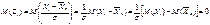
и 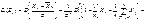
| х0-х1 | х1-х2 | х2-х3 | ... | хi-1-хi | ... | хs-1-хs | |

| 
| 
| ... | 
| ... | 
| , |
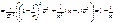 . Очевидно, что
. Очевидно, что  даже для выборок небольшого объема. Поэтому распределение
даже для выборок небольшого объема. Поэтому распределение 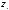 можно считать близким к нормированному нормальному распределению. Тогда случайная величина
можно считать близким к нормированному нормальному распределению. Тогда случайная величина 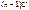 представляет собой сумму квадратов n случайных величин Zi, каждая из которых имеет нормальное распределение, близкое к нормированному. Следовательно, можно считать, что величина (n-1)U имеет распределение Пирсона (
представляет собой сумму квадратов n случайных величин Zi, каждая из которых имеет нормальное распределение, близкое к нормированному. Следовательно, можно считать, что величина (n-1)U имеет распределение Пирсона ( - распределение) с k степенями свободы. Число степеней свободы k определяется как разность между числом суммируемых случайных величин и числом линейных связей, ограничивающих свободу изменения этих величин. В данном случае имеется только одна линейная связь:
- распределение) с k степенями свободы. Число степеней свободы k определяется как разность между числом суммируемых случайных величин и числом линейных связей, ограничивающих свободу изменения этих величин. В данном случае имеется только одна линейная связь: 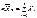 . Поэтому
. Поэтому  и
и  . Тогда распределение случайной величины Т может быть представлено в виде
. Тогда распределение случайной величины Т может быть представлено в виде 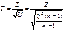 . Следовательно (см. п. 5.6), можно считать, что случайная величина T имеет распределение Стьюдента с
. Следовательно (см. п. 5.6), можно считать, что случайная величина T имеет распределение Стьюдента с 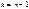 степенями свободы, что и требовалось доказать. Зададим доверительную вероятность ᴕ. Потребуем, чтобы значение случайной величины T с вероятностью ᴕ было бы меньше поабсолютной величине некоторого значения tᴕ, то есть
степенями свободы, что и требовалось доказать. Зададим доверительную вероятность ᴕ. Потребуем, чтобы значение случайной величины T с вероятностью ᴕ было бы меньше поабсолютной величине некоторого значения tᴕ, то есть  . Геометрическая интерпретация этого равенства приведена на рис. 33.
. Геометрическая интерпретация этого равенства приведена на рис. 33.
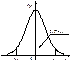 Следует отметить, что величина tᴕ может быть найдена только численно. Результаты численных расчетов
Следует отметить, что величина tᴕ может быть найдена только численно. Результаты численных расчетов 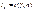 в зависимости от доверительной вероятности ᴕ и объема выборки n представлены в прил. 8.Поскольку
в зависимости от доверительной вероятности ᴕ и объема выборки n представлены в прил. 8.Поскольку 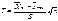 , то рассматриваемое равенство можно переписать в виде
, то рассматриваемое равенство можно переписать в виде
 . После преобразований получим
. После преобразований получим
 или
или 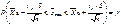
Отсюда следует, что с вероятностью (надежностью) ᴕ можно утверждать, что интервал 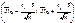 является доверительным для оценки математического ожидания
является доверительным для оценки математического ожидания 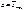 . Величина
. Величина  характеризует здесь точность оценки. Значит, интервальную оценку параметра
характеризует здесь точность оценки. Значит, интервальную оценку параметра 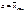 с заданной надежностью ᴕ для случая, когда параметр
с заданной надежностью ᴕ для случая, когда параметр  неизвестен, можно записать следующим образом:
неизвестен, можно записать следующим образом:
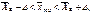 где
где  Замечание. При неограниченном возрастании n распределение Стьюдента стремится к нормальному. Уже при n >30 распределение Стьюдента можно заменить нормальным. В практических расчетах при n >30 вместо значения tᴕ можно использовать аргумент функции Лапласа t, удовлетворяющий условию Ф(t)= ᴕ/2, а неизвестное значение
Замечание. При неограниченном возрастании n распределение Стьюдента стремится к нормальному. Уже при n >30 распределение Стьюдента можно заменить нормальным. В практических расчетах при n >30 вместо значения tᴕ можно использовать аргумент функции Лапласа t, удовлетворяющий условию Ф(t)= ᴕ/2, а неизвестное значение  заменять его оценкой, то есть S. Однако для малых выборок (n <30) при неизвестном
заменять его оценкой, то есть S. Однако для малых выборок (n <30) при неизвестном 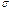 замена распределения Стьюдента нормальным приводит к грубым ошибкам, а точнее, к неоправданному сужению доверительного интервала, поэтому при малом n и неизвестном
замена распределения Стьюдента нормальным приводит к грубым ошибкам, а точнее, к неоправданному сужению доверительного интервала, поэтому при малом n и неизвестном  при оценке математического ожидания нормального распределения случайной величины следует пользоваться распределением Стьюдента.
при оценке математического ожидания нормального распределения случайной величины следует пользоваться распределением Стьюдента.
|
|
|
|
|
|


