 |
Тригонометрическая и показательная форма комплексного числа.
|
|
|
|
ОДОБРЕНО
Цикловой методической комиссией
общеобразовательных и естественнонаучных
дисциплин:
Протокол № ___
от «____» _________________ 2016 г.
Председатель ЦМК:
_____________ Криницына Н.А.
Краткий курс лекций
«МАТЕМАТИКА»
для специальностей:
26.02.06 «Эксплуатация судового электрооборудования и средств автоматики»
23.02.03 «Техническое обслуживание и ремонт автомобильного транспорта»
23.02.01 «Организация перевозок и управление на транспорте (по видам)»
26.02.05 «Эксплуатация судовых энергетических установок»
26.02.03 «Судовождение»
Преподаватель:
Абраменкова В.П..
Пермь
2016 г.
ЦЕЛЬ, ПРЕДМЕТ И ЗАДАЧИ ДИСЦИПЛИНЫ
«Математика» является основной дисциплиной цикла математических и естественнонаучных дисциплин.
Цели изучения дисциплины состоят в овладении студентами:
· базовыми знаниями в области математики как основы фундаментальных знаний;
· навыками решения задач;
· навыками самостоятельной работы с математической литературой.
Целью изучения также является формирование научного мировоззрения студентов.
Предмет дисциплины составляют основные понятия, определения, теоремы разделов математики и методы решения задач.
Задачи дисциплины состоят в обучении студентов:
· основным понятиям, определениям и теоремам разделов математики;
· умениям использовать полученные знания при решении задач и изучении общенаучных дисциплин и дисциплин специальности;
· умениям использовать систему знаний дисциплины для адекватного математического моделирования различных, в том числе экономических, процессов.
ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ
В результате изучения дисциплины «Математика» студент должен:
|
|
|
а) иметь представление об основах:линейной алгебры; аналитической геометрии на плоскости и в пространстве; анализа бесконечно малых величин; дифференциального исчисления функций одной переменной; дифференциального исчисления функции нескольких переменных; интегрального исчисления функции одной и нескольких переменных; дифференциальных уравнений; теории рядов; теории вероятностей и математической статистики.
б) знать: основные понятия, теоремы, методы и правила решения типовых задач изучаемых разделов математики.
в) уметь: применять математические методы к решению теоретических и практических задач; применять полученные знания для решения задач общенаучных и специальных дисциплин.
г) приобрести навыки в решении задач и оценки полученных результатов.
д) владеть, иметь опыт использования необходимых вычислительных средств, таблиц и справочников при производстве расчётов.
Тезисы лекций
Понятие комплексного числа
Комплексное число имеет вид 
, где 
и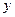 
– действительные числа,
– мнимая единица, 
Число называется действительной частью ( 
) комплексного числа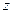 
, число 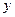называется мнимой частью ( 
) комплексного числа .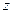
Геометрическая интерпретация комплексного числа.
. Комплексные числа изображаются на комплексной плоскости:
Комплексная плоскость состоит из двух осей:
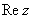– действительная ось
– мнимая ось
Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел.
Алгебраическая форма комплексного числа имеет вид .
1.Сложение комплексных чисел.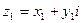 
и 
2. Вычитание комплексных чисел. 
3. Умножение комплексных чисел. 
· 
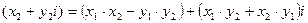
Деление комплексных чисел.
Тригонометрическая и показательная форма комплексного числа.
Любое комплексное число (кроме нуля) можно записать в тригонометрической форме: 
, где 
– это модуль комплексного числа, а 
– аргумент комплексного числа. Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти.
|
|
|
Модулем комплексного числа 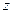называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа z стандартно обозначают: или r
По теореме Пифагора модуль комплексного числа равен: 
.
Примечание: модуль комплексного числа представляет собой обобщение понятия модуля действительного числа, как расстояния от точки до начала координат.
Аргументом комплексного числа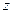 называетсяугол между положительной полуосью действительной оси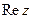 
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 
.
Аргумент комплексного числа 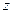стандартно обозначают: , где 
.
|
|
|
