Главная | Обратная связь | Поможем написать вашу работу!

Показательная форма комплексного числа.

Любое комплексное число (кроме нуля) можно записать в показательной форме: , где – это модуль комплексного числа, а – аргумент комплексного числа.

· Действия с комплексными числами в тригонометрической форме.

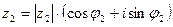1. Умножение. П равила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел: и , нужно перемножить их модули и сложить аргументы:

2. Деление. П равила деления комплексных чисел, представленных в тригонометрической форме: чтобы найти частное чисел: и 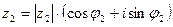, нужно разделить их модули и вычесть аргументы:

3. Возведение в натуральную степень п справедлива формула:

4. Извлечение корня: , где

Действия с комплексными числами в показатедьной форме.

1. Умножение. П равила умножения комплексных чисел, представленных в показательной форме: чтобы найти произведение чисел: и , нужно перемножить их модули и сложить аргументы:

3. Возведение в натуральную степень п:

4. Извлечение корня: , где

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

МАТРИЦЫ

Прямоугольная таблица чисел, содержащая т строк и п столбцов, называется матрицей размера т х п: .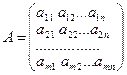

Каждый элемент матрицы снабжается двумя индексами: первый указывает номер строки, а второй – номер столбца, в которых расположен этот элемент.

Две матрицы называются равными, если числа их строк и столбцов совпадают и если равны элементы, расположенные на соответствующих местах этих матриц.

Если число столбцов матрицы п равно числу ее строк, то матрицу называют квадратной матрицей порядка п. Элементы квадратной матрицы порядка п образуют ее главную диагональ.

Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю. Диагональная матица называется единичной, если все ее элементы, расположенные на главной диагонали, равны единице.

Матрица называется транспонированной для матрицы А если она получена из матрицы А путем перестановки местами строк и столбцов.

Действие над матрицами:

1) Умножение матрицы на число. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число.

2) Сложение матриц. Суммой матриц А и В одинаковых размеров называется матрица, элементы которой равны суммам элементов матриц А и В, расположенных на соответствующих местах.

3) Умножение матриц. Матрицу А можно умножить на матрицу В только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица С, у которой столько же строк, сколько их матрице А, и столько же столбцов, сколько их в матрице В, а элементы матрицы С вычисляются по формуле:

т.е. для получения элемента , расположенного в i -строке и j -омстолбце матрицы С, надо элементы i -ой строки матрицы А умножить на соответствующие элементы j -го столбца матрицы В и полученные произведения сложить.

ОПРЕДЕЛИТЕЛИ

Любой квадратной матрице порядка п ставится в соответствие число, называемое определителем этой матрицы. Определитель записывается в виде квадратной таблицы и вычисляется по определенному правилу.

Матрица называется невырожденной если ее определитель неравен нулю.

Минором элемента определителя n -го порядка называется определитель (п – 1)-го порядка, который получается в результате вычеркивания в определителе n -го порядка строки и столбца, содержащих элемент .