 |
Некоторые достаточные признаки сходимости рядов с положительными членами
|
|
|
|
1. Признак сравнения. Рассмотрим два числовых ряда с положительными членами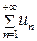 
и 
. Если при всех 
, начиная с некоторого номера,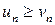 
, то из сходимости ряда 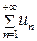следует сходимость ряда . Наоборот, из расходимости ряда следует расходимость ряда .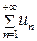
При использовании признака сравнения нужно иметь эталонный ряд, про сходимость которого известно заранее. В качестве таких рядов чаще всего берут обобщенный гармонический ряд 
, который сходится при 
и расходится при 
, или геометрический ряд 
, который сходится при 
и расходится при 
.
2. Признак сходимости Даламбера. Пусть для ряда с положительными членами 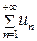существует предел 
. Тогда: если 
, то ряд сходится; если 
, то ряд расходится. При 
признак Даламбера ответа не дает: ряд может, как сходиться, так и расходиться.
3. П ризнаки сходимости знакопеременных рядов
Если члены числового ряда имеют разные знаки, то ряд называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд вида 
, где 
.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин членов ряда, т.е. ряд вида 
. Если ряд из абсолютных величин расходится, а сам ряд сходится, то его называют условно сходящимся. Исследование знакопеременного ряда начинают с исследования на сходимость ряда из абсолютных величин методами, которые применяются для рядов с положительными членами. Если такой ряд сходится, то получен ответ: ряд сходится абсолютно.
Если ряд из абсолютных величин расходится, то для знакочередующегося ряда можно применить признак Лейбница: если члены ряда стремятся к нулю, монотонно убывая, то ряд сходится, по крайней мере, условно.
ОСНОВЫ ТеориИ вероятностей
|
|
|
Случайные события
В результате многократного повторения одних и тех же условий, которые носят название испытаний или опытов, можно наблюдать появление или непоявление в них некоторого события. Все события подразделяются на три вида:
· достоверные, которые обязательно происходят в результате испытания;
· невозможные, которые никогда не происходят в результате испытания;
· случайные, которые могут произойти, а могут не произойти в результате испытания.
Теория вероятностей занимается изучением закономерностей массовых однородных случайных
событий.
Будем обозначать случайные события прописными буквами А, В, С или 
. Случайные события называются несовместными если появление одного из них в результате испытания исключает появление другого. Два события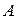 
или 
называются противоположными, если они несовместны и непоявление одного из них в результате испытания означает появление другого. Если события таковы, что в результате испытания обязательно произойдет одно из них, то они образуют полную группу.
Классическая вероятность
Каждый из равновозможных результатов испытаний (опытов) называется элементарным исходом.
Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление такого события.
Количественной мерой возможности появления некоторого случайного события служит вероятность.
При классическом определении за вероятность события А принимается отношение числа благоприятствующих этому событию элементарных исходов (m) к общему числу возможных исходов (n): 
.
Классическая вероятность обладает следующими свойствами:
1) вероятность достоверного события равна единице;
2) вероятность невозможного события равна нулю;
3) вероятность случайного события определяется неравенством 
.
Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются формулы комбинаторики:
|
|
|
- если составляются такие комбинации из n элементов по m, которые отличаются друг то друга только составом элементов, то они называются сочетаниями
; - если комбинации отличаются и составом элементов, и порядком их следования, то они называются размещениями:
; - если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановками:
.
|
|
|
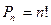