 |
Математические модели и характеристики погрешностей
|
|
|
|
В общем случае результаты измерений и их погрешности должны рассматриваться как функции, изменяющиеся во времени случайным образом, т.е. случайные функции, или, как принято говорить в математике, случайные процессы. Поэтому математическое описание результатов и погрешностей измерений (т.е. их математические модели) должно строиться на основе теории случайных процессов. Изложим основные моменты теории случайных функций.
Случайным процессом X(t) называется процесс (функция), значение которого при любом фиксированном значении t = tQ является случайной величиной X(t 
). Конкретный вид процесса (функции), полученный в результате опыта, называется реализацией.
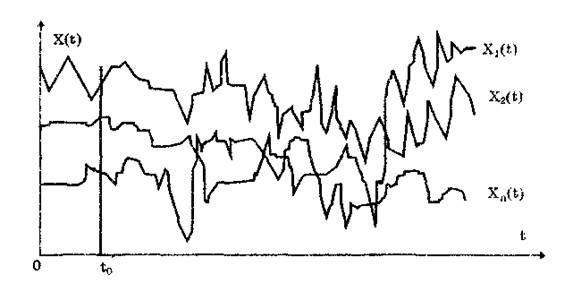
Рис. 4. Вид случайных функций
Каждая реализация является неслучайной функцией времени. Семейство реализаций при каком-либо фиксированном значении времени t (рис. 4) представляет собой случайную величину, называемую сечением случайной функции, соответствующим моменту времени t 
. Следовательно, случайная функция совмещает в себе характерные признаки случайной величины и детерминированной функции. При фиксированном значении аргумента она превращается в случайную величину, а в результате каждого отдельного опыта становится детерминированной функцией.
Математическим ожиданием случайной функции X(t) называется неслучайная функция которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения:
(7)
где p(x, t) — одномерная плотность распределения случайной величины х в соответствующем сечении случайного процесса X(t).
Дисперсией случайной функции X(t) называется неслучайная функция значение которой для каждого момента времени равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно m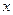 
(t).
|
|
|
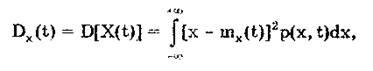(8)
Корреляционная функция — неслучайная функция R(t, t') двух аргументов t и t', которая при каждой паре значений аргументов равна ковариации соответствующих сечений случайного процесса:
(9)
Корреляционная функция, называемая иногда автокорреляционной, описывает статистическую связь между мгновенными значениями случайной функции, разделенными заданным значением времени т = t'-t. При равенстве аргументов корреляционная функция равна дисперсии случайного процесса. Она всегда неотрицательна.
Случайные процессы, протекающие во времени однородно, частные реализации которых с постоянной амплитудой колеблются вокруг средней функции, называются стационарными. Количественно свойства стационарных процессов характеризуются следующими условиями:
• математическое ожидание постоянно;
• дисперсия по сечениям является постоянной величиной;
• корреляционная функция зависит не от значения аргументов, а только от промежутка.
Важной характеристикой стационарного случайного процесса является его спектральная плотность S(w), которая описывает частотный состав случайного процесса при w>О и выражает среднюю мощность случайного процесса, приходящуюся на единицу полосы частот:
(10)
Спектральная плотность стационарного случайного процесса является неотрицательной функцией частоты. Корреляционная функция может быть выражена через спектральную плотность
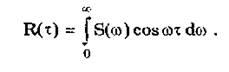(11)
При построении математической модели погрешности измерений следует учитывать всю информацию о проводимом измерении и его элементах.
Каждая из них может быть обусловлена действием нескольких различных источников погрешностей и в свою очередь состоять также из некоторого числа составляющих.
Для описания погрешностей используются теория вероятностей и математическая статистика, однако прежде необходимо сделать ряд существенных оговорок:
|
|
|
• применение методов математической статистики к обработке результатов измерений правомочно лишь в предположении о независимости между собой отдельных получаемых отсчетов;
• большинство используемых в метрологии формул теории вероятностей правомерны только для непрерывных распределений, в то время как распределения погрешностей вследствие неизбежного квантования отсчетов, строго говоря, всегда дискретны, т.е. погрешность может принимать лишь счетное множество значений.
Таким образом, условия непрерывности и независимости для результатов измерений и их погрешностей соблюдаются приближенно, а иногда и не соблюдаются. В математике под термином "непрерывная случайная величина" понимается существенно более узкое, ограниченное рядом условий понятие, чем "случайная погрешность" в метрологии.
В метрологии принято различать три группы характеристик и параметров погрешностей. Первая группа—задаваемые в качестве требуемых или допускаемых нормы характеристик погрешности измерений (нормы погрешностей). Вторая группа характеристик— погрешности, приписываемые совокупности выполняемых по определенной методике измерений. Характеристики этих двух групп применяются в основном при массовых технических измерениях и представляют собой вероятностные характеристики погрешности измерений. Третья группа характеристик—статистические оценки погрешностей измерений отражают близость отдельного, экспериментально полученного результата измерения к истинному значению измеряемой величины. Они используются в случае измерений, проводимых при научных исследованиях и метрологических работах.
Совокупность формул, описывающих состояние, движение и взаимодействие объектов, полученных в рамках выбранных физических моделей на основе законов физики, будем называть математической моделью объекта или процесса. Процесс создания математической модели можно разделить на ряд этапов:
1) составление формул и уравнений, описывающих состояние, движение и взаимодействие объектов в рамках построенной физической модели. Этап включает запись в математических терминах сформулированных свойств объектов, процессов и связей между ними;
|
|
|
2) исследование математических задач, к которым приходят на первом этапе. Основным вопросом здесь является решение прямой задачи, т.е. получение численных данных и теоретических следствий. На этом этапе важную роль приобретают математический аппарат и вычислительная техника (компьютер).
3) выяснение того, согласуются ли результаты анализа и вычислений или следствия из них с результатами наблюдений в пределах точности последних, т.е. удовлетворяет ли принятая физическая и (или) математическая модель практике—основному критерию истинности наших представлений об окружающем мире.
Отклонение результатов расчетов от результатов наблюдений свидетельствует либо о неправильности применяемых математических методов анализа и расчета, либо о неверности принятой физической модели. Выяснение источников ошибок требует большого искусства и высокой квалификации исследователя.
Часто при построении математической модели некоторые ее характеристики или связи между параметрами остаются неопределенными вследствие ограниченности наших знаний о физических свойствах объекта. Например, оказывается, что число уравнений, описывающих физические свойства объекта или процесса и связи между объектами, меньше числа физических параметров, характеризующих объект. В этих случаях приходится вводить дополнительные соотношения, характеризующие объект исследования и его свойства, иногда даже пытаться угадать эти свойства, для того, чтобы задача могла быть решена и результаты соответствовали результатам опыта в пределах заданной погрешности.
|
|
|
