 |
Вероятностное описание результатов и случайных погрешностей
|
|
|
|
Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины.
Рассмотрим формирование дифференциального закона на примере измерений с многократными наблюдениями. Пусть произведено n последовательных наблюдений одной и той же величины x и получена группа наблюдений 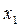 ,
, 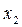 ,
, 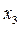 ,….,
,…., 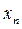 . Каждое из значений
. Каждое из значений 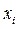 содержит ту или иную случайную погрешность. Расположим результаты наблюдений в порядке их возрастания, от xmin до xmax и найдем размах ряда L =xmax − xmin. Разделив размах ряда на k равных интервалов Δl = L/k, подсчитаем количество наблюдений
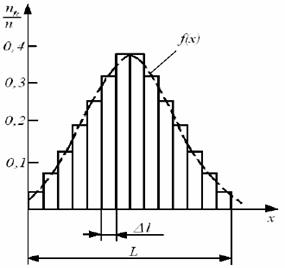
содержит ту или иную случайную погрешность. Расположим результаты наблюдений в порядке их возрастания, от xmin до xmax и найдем размах ряда L =xmax − xmin. Разделив размах ряда на k равных интервалов Δl = L/k, подсчитаем количество наблюдений 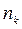 , попадающих в каждый интервал. Оптимальное число интервалов определяют по формуле Стерджесса k = 1 + 3,3 lg n. Изобразим полученные результаты графически, нанеся на ось абсцисс значения физической величины и обозначив границы интервалов, а на ось ординат – относительную частоту попаданий
, попадающих в каждый интервал. Оптимальное число интервалов определяют по формуле Стерджесса k = 1 + 3,3 lg n. Изобразим полученные результаты графически, нанеся на ось абсцисс значения физической величины и обозначив границы интервалов, а на ось ординат – относительную частоту попаданий 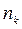 /n. Построив на диаграмме прямоугольники, основанием которых является ширина интервалов, а высотой
/n. Построив на диаграмме прямоугольники, основанием которых является ширина интервалов, а высотой 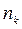 /n, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте.
/n, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте.
На рис.5 показана полученная в одном из опытов гистограмма, построенная на основании результатов 100 наблюдений, сгруппированных в таблице 1.
Таблица 1
| Номер интервала | |||||||
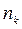
| |||||||
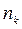 / n / n
| 0,06 | 0,12 | 0,18 | 0,25 | 0,17 | 0,14 | 0,08 |
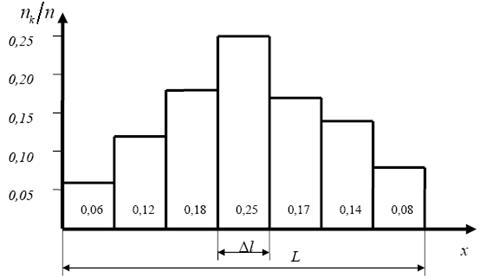
Рис. 5. Гистограмма частот
Если распределение случайной величины х статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает то, что, построив гистограмму один раз, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам.
|
|
|
При бесконечном увеличении числа наблюдений n→∞ и бесконечному уменьшению ширины интервалов Δl → 0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f(x), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее,– дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:
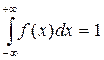 (12)
(12)
 или
или 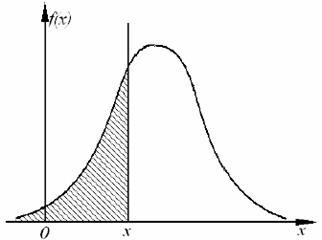
Рис. 6. Кривая плотности распределения вероятностей
Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения f (x), то вероятность Ρ попадания случайной величины х в интервал от 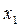 до
до 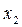 можно записать в следующем виде:
можно записать в следующем виде:
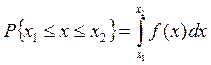 (13)
(13)
Графически эта вероятность выражается отношением площади, лежащей под кривой f(x) в интервале от 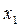 до
до 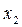 к общей площади, ограниченной кривой распределения. Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал[−∞;+∞] равна единице, т.е. представляет собой достоверное событие.
к общей площади, ограниченной кривой распределения. Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал[−∞;+∞] равна единице, т.е. представляет собой достоверное событие.
Вероятность этого события называется функцией распределения случайной величины и обозначается F(x). Функцию распределения F(x) иногда называют также интегральной функцией распределения (рис. 3(а)). В терминах интегральной функции распределения имеем:
|
|
|
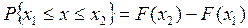 (14)
(14)
т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.
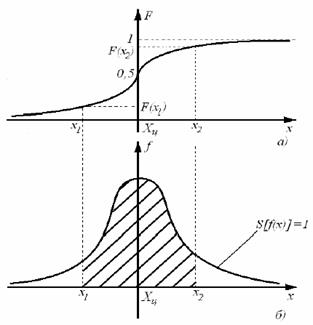
Рис. 7. Интегральная (а) и дифференциальная (б) функции распределения случайной величины
Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина 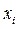 в i-м опыте принимает значение, меньшее х. График интегральной функции распределения имеет следующие свойства:
в i-м опыте принимает значение, меньшее х. График интегральной функции распределения имеет следующие свойства:
ü неотрицательная, т.е. 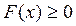 ;
;
ü неубывающая, т.е. 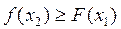 , если
, если 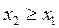 ;
;
ü диапазон ее изменения: от 0 до 1, т.е. 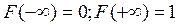 ;
;
ü вероятность нахождения случайной величины х в диапазоне от 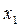 до
до 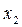 :
: 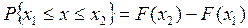 .
.
Запишем функцию распределения через плотность:
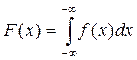 (15)
(15)
Площадь, ограниченная кривой распределения, лежащая левее точки x (х–текущая переменная), отнесенная к общей площади, есть не что иное, как интегральная функция распределения F(x)=P{xi<x}. Плотность распределения вероятностей f(x) называют дифференциальной функцией распределения (рис. 3(б)).
Плотность распределения вероятностей 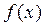 называют дифференциальной функцией распределения:
называют дифференциальной функцией распределения:
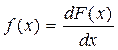 (16)
(16)
Функция распределения является самым универсальным способом описания поведения результатов измерений и случайных погрешностей. Однако для их определения необходимо проведение весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины специальными параметрами, основными из которых являются:
· центр распределения;
· начальные и центральные моменты и производные от них коэффициенты – математическое ожидание (МО);
· среднее квадратическое отклонение (СКО);
· эксцесс;
· контрэксцесс;
· коэффициент асимметрии.
Координата центра распределения 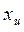 определяет положение случайной величины на числовой оси и может быть найдена несколькими способами.
определяет положение случайной величины на числовой оси и может быть найдена несколькими способами.
Наиболее фундаментальным является определение центра по принципу симметрии вероятностей, т.е. нахождение такой точки 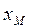 на оси х, слева и справа от которой вероятности появления различных значений случайных погрешностей равны между собой и составляют
на оси х, слева и справа от которой вероятности появления различных значений случайных погрешностей равны между собой и составляют 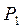 =
= 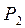 =0,5:
=0,5:
|
|
|
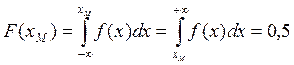 (17)
(17)
Точка 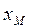 называется медианой, или 50%-ным квантилем. Для его нахождения у распределения случайной величины должен существовать только нулевой начальный момент. Координата
называется медианой, или 50%-ным квантилем. Для его нахождения у распределения случайной величины должен существовать только нулевой начальный момент. Координата 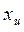 может быть определена и как центр тяжести распределения, т.е. как математическое ожиданиеслучайной величины. Это такая точка
может быть определена и как центр тяжести распределения, т.е. как математическое ожиданиеслучайной величины. Это такая точка 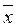 , относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая
, относительно которой опрокидывающий момент геометрической фигуры, огибающей которой является кривая 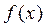 , равен нулю:
, равен нулю:
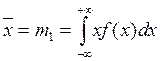 =0 (18)
=0 (18)
При симметричной кривой плотности распределения вероятностей 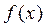 оценкой центра распределения может служить абсцисса модыраспределения, т.е. координата максимума плотности распределения
оценкой центра распределения может служить абсцисса модыраспределения, т.е. координата максимума плотности распределения 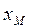 . Однако есть распределения, у которых не существует моды, например, равномерное. Распределения с одним максимумом называются одномодальными, с двумя – двухмодальные. Те распределения, у которых в средней части расположен не максимум, а минимум, называются антимодальными. Для двухмодальных распределений применяется оценка центра в виде центра сгибов:
. Однако есть распределения, у которых не существует моды, например, равномерное. Распределения с одним максимумом называются одномодальными, с двумя – двухмодальные. Те распределения, у которых в средней части расположен не максимум, а минимум, называются антимодальными. Для двухмодальных распределений применяется оценка центра в виде центра сгибов:
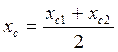 (19)
(19)
где 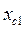 ,
, 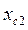 -сгибы, т.е. абсциссы точек, в которых распределение достигает максимумов.
-сгибы, т.е. абсциссы точек, в которых распределение достигает максимумов.
При выборе оценки центра распределения необходимо учитывать ее чувствительность к наличию промахов в обрабатываемой совокупности данных. Исключительно чувствительны к наличию промахов: оценка в виде центра размаха 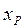 (определяется по наблюдениям, наиболее удаленным от центра, каковыми и являются промахи); оценка в виде среднего арифметического (ослабляется лишь в
(определяется по наблюдениям, наиболее удаленным от центра, каковыми и являются промахи); оценка в виде среднего арифметического (ослабляется лишь в 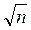 раз). Защищенными от влияния промахов являются квантильные оценки: медиана
раз). Защищенными от влияния промахов являются квантильные оценки: медиана 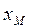 и центр сгибов
и центр сгибов 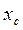 , поскольку они не зависят от координат промахов. При статистической обработке данных важно использовать наиболее эффективные, т.е. имеющие минимальную дисперсию, оценки центра распределения, так как погрешность в определении
, поскольку они не зависят от координат промахов. При статистической обработке данных важно использовать наиболее эффективные, т.е. имеющие минимальную дисперсию, оценки центра распределения, так как погрешность в определении 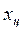 влечет за собой неправильную оценку СКО, границ доверительного интервала, эксцесса и т.д.
влечет за собой неправильную оценку СКО, границ доверительного интервала, эксцесса и т.д.
Все моменты представляют собой некоторые средние значения, причем, если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра распределения – то центральными.
|
|
|
Начальные моменты k- го порядка определяются формулами:
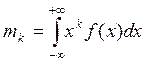 или
или 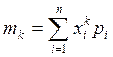 (20)
(20)
где 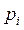 – вероятность появления дискретной величины. Первая формула относится к непрерывным, а вторая к дискретным случайным величинам. Из начальных моментов наибольший интерес представляет математическое ожидание (МО) случайной величины (k = 1):
– вероятность появления дискретной величины. Первая формула относится к непрерывным, а вторая к дискретным случайным величинам. Из начальных моментов наибольший интерес представляет математическое ожидание (МО) случайной величины (k = 1):
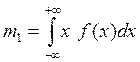 или
или 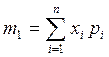 (21)
(21)
Центральные моменты k -го порядка рассчитываются по формулам:
 или
или 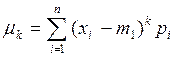 (22)
(22)
Из центральных моментов особенно важную роль играет второй момент
(k =2), дисперсия случайной величины D:
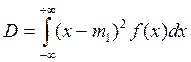 или
или 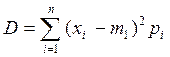 (23)
(23)
Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии – средним квадратическим отклонением (СКО) σ = 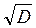 , которое имеет размерность самой случайной величины.
, которое имеет размерность самой случайной величины.
Третий центральный момент
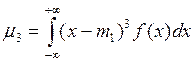 или
или 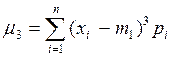 (24)
(24)
служит характеристикой асимметрии или скошенности распределения.
Четвертый центральный момент
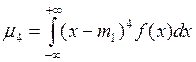 или
или 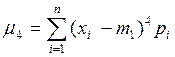 (25)
(25)
служит для характеристики плосковершинности или островершинности
распределения.
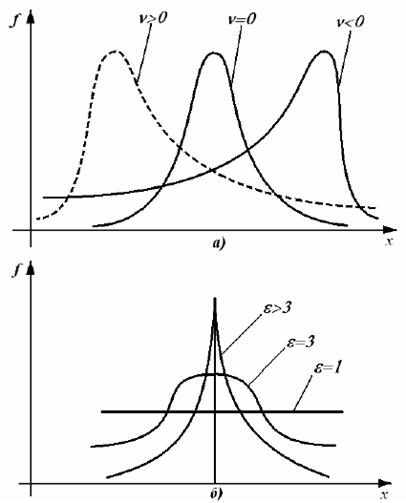
Рис. 8. Вид дифференциальной функции распределения
при различных значениях коэффициента асимметрии (а) и эксцесса (б).
РАСЧЕТНАЯ ЧАСТЬ
Задача 1.Дан график функции распределения F (x) случайной величины X:
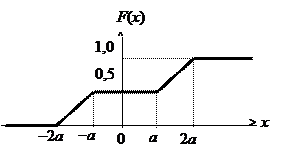 |
Определите вероятности следующих событий: Р 1 = Р (Х £ a), Р 2 = Р (0 £ Х £ a), Р 3 = Р (Х > 0), Р 4 = Р (Х < 0), Р 5 = Р (Х = 2 a). Найдите аналитическое выражение функции плотности вероятности f (x). Определите значения математического ожидания М (Х) и СКО s.
Решение: F (x) = Р (X < x) [= P (X £ x) для непрерывных величин];
По формуле 13 найдем вероятность попадания случайной величины:
Р (x 1 £ Х £ x 2) = F (x 2) – F (x 1);
в первый интервал: Р 1 = 0,5;
во второй: Р 2 = 0;
в третий: Р 3 = Р (0 < Х < +¥) = F (+¥) – F (0) = 0,5;
в четвертый: Р 4 = Р (–¥ < Х < 0) = F (0) – F (–¥) = 0,5;
в пятый: Р 5 = 0.
По формуле 16 найдем плотность распределения вероятностей:
f (x) = d F /d x;
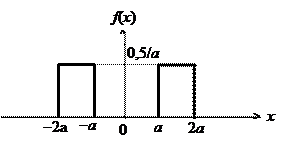 |
f (x) = 0 при x < –2 a, – a < x < a, x > 2 a;
f (x) = 0,5 / a при –2 a £ x £ – a, a £ x £ 2 a;
По формуле 21 найдем математическое ожидание случайной величины:
М (Х) 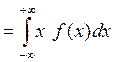 = (0,5 / 2 a) (a 2 – 4 a 2 + 4 a 2 – a 2) = 0
= (0,5 / 2 a) (a 2 – 4 a 2 + 4 a 2 – a 2) = 0
Для нахождения СКО s нам потребуется для начала найти дисперсию случайной величины по формуле 23:
D (Х) 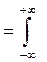 [ x – M (X)] 2 f (x) d x = (0,5 / 3 a) (– a 3 + 8 a 3 + 8 a 3 – a 3) = 7 a 2 / 3
[ x – M (X)] 2 f (x) d x = (0,5 / 3 a) (– a 3 + 8 a 3 + 8 a 3 – a 3) = 7 a 2 / 3
А теперь можно найти и СКО s:
σ = 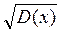 =
= 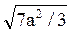 » 1,53 a;
» 1,53 a;
Ответ: М (Х) = 0, s» 1,53 a
Задача 2. Случайная погрешность D распределена по закону равномерной плотности. Известны значения вероятностей двух событий — Р 1 и Р 2. Р 1 = Р (D< –5 мкВ) = 0,3; Р 2 = Р (D > 5 мкВ) = 0,2. Определите значения дисперсии D (D) и вероятности Р 3 = Р (D > 0).
|
|
|
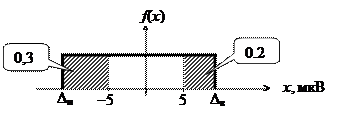 Решение:
Решение:
плотность вероятности f (x) = const = 1 / (Dв – Dн);
Р 1 = 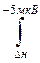 f (x) d x = (–5 мкВ – Dн) / (Dв – Dн);
f (x) d x = (–5 мкВ – Dн) / (Dв – Dн);
Р 2 = 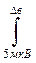 f (x) d x = (Dв – 5 мкВ) / (Dв – Dн);
f (x) d x = (Dв – 5 мкВ) / (Dв – Dн);
Р 1 + Р 2 = (Dв – Dн – 10 мкВ) / (Dв – Dн) = 1 – 10 мкВ / (Dв – Dн);
Dв – Dн = 10 мкВ / (1 – Р1 – Р2) = 20 мкВ;
Dв = Р2 (Dв – Dн) + 5 мкВ = 9 мкВ;
Dн = –11 мкВ;
Математическое ожидание: М (D) = (Dв + Dн) / 2 = –1 мкВ;
Дисперсия: D (D) = (Dв – Dн)2 / 12» 33 мкВ2;
Р 3 = 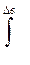 f (x) d x = Dв / (Dв – Dн) = 0,45.
f (x) d x = Dв / (Dв – Dн) = 0,45.
Ответ: D (D) =33мкВ  , Р 3 = 0,45.
, Р 3 = 0,45.
Задача 3. Сопротивление R составлено из параллельно включенных сопротивлений R1 и R2, математические ожидания и средние квадратические отклонения которых известны: m1 = 12 Ом; m2 = 15 Ом; s1 = 1 Ом; s2 = 0,5 Ом. Найдите математическое ожидание mR и среднюю квадратическую погрешность sR сопротивления R.
Решение. При параллельном соединении
R = R1 R2 / (R1 + R2)
Воспользуемся формулами для нахождения математического ожидания mу и среднего квадратического отклонения sу
mу = F (mу1, mу2, …, mуn)
n
sу = Ö å (¶F / ¶yi)2m s2yi,
i = 1
где (¶F / ¶yi)m - частная производная функции F (у1, у2, …, уn) по yi, взятая в точке (mу1, mу2, …, mуn).
Тогда
mR = m1 m2 / (m1 + m2) = 12× 15 / (12 + 15) = 6,67 Ом.
Для нахождения sR вычислим сначала частные производные:
(¶R / ¶R1)m = (¶R2 / R1 + R2)2m =(m2 / m1+ m2)2 = 0,31,
(¶R / ¶R2)m = (¶R1 / R1 + R2)2m =(m1 / m1+ m2)2 = 0,20.
Далее вычислим среднюю квадратическую погрешность sR:
sR = Ö (¶R / ¶R1)2m s21+ (¶R / ¶R2)2m s22 = Ö 0,312 × 12 + 0,22 × 0,52 = 0,33Ом.
Ответ: mR=6,67 Ом, sR=0,33 Ом.
Задача 4. Определите относительную погрешность измерения в начале шкалы (для 30 делений) для прибора класса 0,5, имеющего шкалу 100 делений. Насколько эта погрешность больше погрешности на последнем – сотом делении шкалы прибора?
Решение. Для прибора класса 0,5 относительная приведенная погрешность (на 100 делений шкалы):
d = (0,5 × 100) / 100 = 0,5%.
Относительная погрешность измерения в начале шкалы (на 30 делений шкалы):
dзо = (0,5 × 100) / 30 = 1,6%.
dзо > dпр более чем в 3 раза
Ответ: dзо=1,6%, эта погрешность более чем в 3 раза больше погрешности на последнем – сотом делении шкалы прибора.
Задача 5. При поверке ваттметра на постоянном токе действительное значение мощности Р измеряют потенциометром. При этом отдельно измеряют (с помощью шунта) ток в последовательной цепи ваттметра и (с помощью делителя) напряжение в параллельной цепи. Известно, что пределы допускаемых погрешностей для элементов, участвующих в измерениях, следующие: dп потенциометра 0,005%; dн нормального элемента 0,005%; dд делителя напряжения 0,005%; dш шунта 0,01%. Определите относительную погрешность измерения мощности.
Решение. Действительное значение мощности определяется в соответствии с зависимостью
Р = Uд Uш / Кд Rш,
где Uд, Uш – напряжения на делителе и шунте; Кд – коэффициент деления делителя; Rш – сопротивление шунта.
Погрешность измерения напряжения складывается из погрешности потенциометра и погрешности нормального элемента.
dР = Ö (2dп)2 + (2dн) 2 + (dд) 2 + (dш) 2 = Ö (2 0,005) 2 + (2 0,005) 2 + 0,0052 + 0,012 = 0,018%
Ответ: dР=0,018%.
ВЫВОД
Безусловно, измерения в жизни человека имеют большое значение. Где бы мы не находились, чем бы не занимались мы все время что то измеряем, будь то время на часах или километраж на машине.
В этой курсовой работе представлена лишь небольшая часть теории погрешностей и математических моделей.
Начнем с того, что в данной работе мы выяснили, что такое истинное значение физической величины: разница между результатом единичного наблюдения, случайной и систематической погрешностями; значение, идеальным образом отражающее свойство данного объекта, как в количественном, так и в качественном отношении.

|

|
|
 Рассмотрели основную теорию погрешностей, предоставив небольшую классификацию погрешностей.
Рассмотрели основную теорию погрешностей, предоставив небольшую классификацию погрешностей.
 | |||||
 | |||||
 | |||||


 Погрешность
Погрешность

Охарактеризовали стационарный процесс спектральной плотностью, разобрались в корреляционной функции.
Выяснили, что для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины, который имеет две формы: интегральную и дифференциальную. Более подробно разобрали параметры распределения случайных погрешностей измерений, подчиняющихся законам распределения вероятностей.
Охарактеризовали специальные параметры случайных величин, основными из которых являются:
· центр распределения;
· начальные и центральные моменты и производные от них коэффициенты – математическое ожидание (МО) и дисперсию;
· среднее квадратическое отклонение (СКО);
· контрэксцесс.
В общем, мы подытожили все то, что прошли на лекциях и лабораторных работах по теории погрешностей.
Список использованной литературы
1. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений.-2-е изд.,перераб. и доп. –Л.: Энергоатомиздат. Ленингр.отд-ние,1991.-304 с.:ил.
2. Анохина Е.С., Булатов Р.Б., Абдулкина Н.В. Метрология, стандартизация и сертификация: Методическое руководство к подготовке и защите курсовых работ для студентов очной формы обучения.-Альметьевск:АГНИ,2008.-76 с.
3. Бурдун Г.Д., Марков Б.Н. Основы метрологии. Учебное пособие для вузов. Издание третье, переработанное – М.: Изд-во стандартов, 1985. - 256 с.
4. Козлов М.Г. Метрология и стандартизация: Учебник. М., СПб.: Изд-во «Петербургский ин-т печати», 2001. - 372 с.
Для заметок
|
|
|


