Основная задача линейного программирования.

Определение. Линейное программирование (ЛП)— наука о ме­тодах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Определение. Математическое выражение целевой функ­ции и ее ограничений называется математической моделью экономической задачи.

В общем виде математическая модель задачи линейного программирования (ЛП) записывается как

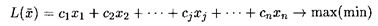
при ограничениях:

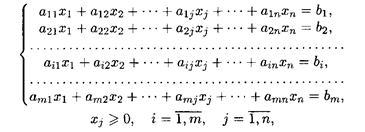
где x_j — неизвестные; a_ij, b_i, c_j — заданные постоянные вели­чины.

Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.

Математическая модель в более краткой записи имеет вид

при ограничениях:

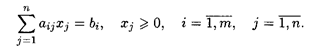
Определение. Допустимым решением (планом) зада­чи линейного программирования называется вектор = (x ₁, x ₂,..., x_п), удовлетворяющий системе ограничений.

Множество допустимых решений образует область допус­тимых решений (ОДР).

Определение. Допустимое решение, при котором целевая функция достигает своего экстремального значения, называ­ется оптимальным решением задачи линейного программиро­вания и обозначается _опт.

Базисное допустимое решение (х ₁, х ₂ ,..., x _r, 0, …, 0) яв­ляется опорным решением, где r — ранг системы ограничений.

Математическая модель задачи ЛП может быть каноничес­кой и неканонической.

 

7.Решение задач линейного программирования графическим методом. Графики функций-ограничений. Линии уровня.

Графический метод решения задач линейного программирования

Наиболее простым и наглядным методом линейного про­граммирования является графический метод. Он применяется для решения задач ЛП с двумя переменными, заданными в не­канонической форме, и многими переменными в канонической форме при условии, что они содержат не более двух свободных переменных.

С геометрической точки зрения в задаче линейного про­граммирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Для нахождения экстремального значения целевой функ­ции при графическом решении задач ЛП используют вектор L () на плоскости Х ₁ ОХ ₂, который обозначим. Этот вектор показывает направление наискорейшего изменения це­левой функции. Другими словами вектор - нормаль линии уровня L ()

где е ₁ и е ₂ — единичные векторы по осям OX ₁ и ОX ₂ соответ­ственно; таким образом, = (∂L/∂х ₁, ∂L/∂х ₂ ). Координатами вектора являются коэффициенты целевой функции L(). Построениелинии уровня будет рассмотрено подробно при решении практических задач.

Алгоритм решения задач

1. Находим область допустимых решений системы ограни­чений задачи.

2. Строим вектор.

3. Проводим линию уровня L ₀, которая перпендикулярна.

4. Линию уровня перемещаем по направлению вектора для задач на максимум и в направлении, противоположном, для задач на минимум.

Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допусти­мых решений. Эта точка, определяющая единственное решение задачи ЛП, и будет точкой экстремума.

Если окажется, что линия уровня параллельна одной из сторон ОДР, то в таком случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Говорят, что такая задача ЛП имеет альтернативный оптимум, и ее решение находится по формуле:

где 0 ≤ t ≤ 1, ₁ и ₂ — оптимальные решения в угловых точках ОДР.

Задача ЛП может быть неразрешима, когда определяющие ее ограничения окажутся противоречивыми.

5. Находим координаты точки экстремума и значение це­левой функции в ней.

Пример 3. Выбор оптимального варианта выпуска изделий

Фирма выпускает 2 вида мороженого: сливочное и шоко­ладное. Для изготовления мороженого используются два ис­ходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице.

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное мороженное, но не бо­лее чем на 100 кг.

Кроме того, установлено, что спрос на шо­коладное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного — 14 р.

Какое количество мороженого каждого вида должна про­изводить фирма, чтобы доход от реализации продукции был максимальным?

Решение. Обозначим: x ₁ - суточный объем выпуска сли­вочного мороженого, кг; x ₂ — суточный объем выпуска шоко­ладного мороженого, кг.

Составим математическую модель задачи.

Цены на мороженное известна: соответственно 16руб и 14руб., поэтому целевая функция будет иметь вид:

Установим ограничения по молоку для мороженного. Расход его на сливочное мороженное - 0,8кг, на шоколадное - 0,5кг. Запас молок 400кг. Поэтому первое неравенство будет иметь вид:

0,8х₁+ 0,5х₂ ≤400 – первое неравенство – ограничение. Аналогично составляются остальные неравенства.

В результате получится система неравенств. что область решения каждого неравенства. Это можно сделать, подставив в каждое из неравенств координаты точки О(0:0). В результате получим:

Фигура OABDEF — область допустимых решений. Строим вектор (16; 14). Линия уровня L ₀ задается уравнением 16x₁+14x₂=Const. Выбираем любое число, например число 0, тогда 16x₁+14x₂=0. На рисунке для линии L₀ выбрано некоторое положительное число, не равное нулю. Все линии уровня параллельны между собой. Вектор нормаль линии уровня.

Перемещаем линию уровня по направлению вектора. Точ­кой выхода L ₀ из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, за­данных уравнениями:

Решая систему, получим координаты точки D (312,5; 300), в которой и будет оптимальное решение, т.е.

при этом

Таким образом, фирма должна выпускать в сутки 312,5 кг сли­вочного мороженого и 300 кг шоколадного мороженого, при этом доход от реализации составит 9 200 р.

8.Сведение произвольной задачи линейного программирования к основной задаче. Преобразование ограничений, заданных неравенствами в соответствующие уравнения.

9.Симплекс-метод. Характеристика и алгоритм метода, применимость его.

Для решения задачи симплекс методом необходимо:

1. Указать способ нахождения оптимального опорного решения

2. Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции будет ближе к оптимальному, т.е. указать способ улучшения опорного решения

3. Задать критерии, которые позволяют своевременно прекратить перебор опорных решений на оптимальном решении или сдать заключение об отсутствии оптимального решения.

Алгоритм симплексного метода решения задач линейного программирования

1. Привести задачу к каноническому виду

2. Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение, в виду несовместимости системы ограничений)

3. Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода

4. Если выполняется признак единственности оптимального решения, то решение задачи заканчивается

5. Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения

10.Транспортная задача. Определение, виды, методы нахождения начального решения транспортной задачи.

Транспортная задача — одна из распространенных задач линейного программирования. Ее цель - разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перево­зок.

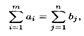
З адача называется закрытой, если: открытой, если:

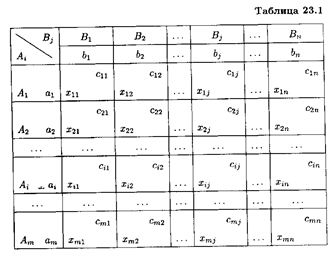
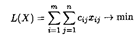Математическая модель закрытой транспортной задачи имеет вид:

при ограничениях:

 

Оптимальным решением задачи является матрица, удовлетворяющая системе ограничений и доставляющая мини­мум целевой функции.

 

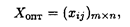
Транспортная задача как задача линей­ного программирования может быть решена симплексным ме­тодом, однако наличие большого числа переменных и ограни­чений делает вычисления громоздкими. Поэтому для решения транспортных задач разработан специальный метод, имеющий те же этапы, что и симплексный метод, а именно:

1. Нахождение исходного опорного решения;

2. Проверка этого решения на оптимальность;

3. Переход от одного опорного решения к другому.

 

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: