Общий вид задач нелинейного программирования

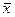Математическая модель задачи нелинейного программиро­вания в общем виде формулируется следующим образом: найти вектор = (х ₁, x ₂, …, x_n), удовлетворяющий системе ограни­чений и доставляющий экстремум (наибольшее или наименьшее зна­чение) целевой функции: L=f(x₁,x₂,x₃,…x_n), где x_j — переменные, j = ; L, f, g_i — заданные функции от n переменных, b_i — фиксированные значения.

В системе ограничений, уравнения и неравенства, а также и целевая функция могут быть сколь угодной сложности.

Нелинейное программирование применяется при прогнози­ровании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудова­ния и т.д.

Для задачи нелинейного программирования нет единого метода решения.

В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, например, такие как:

~ методы множителей Лагранжа, ~ квадратичное и выпуклое программи­рование, ~ градиентные методы,

~ приближенные методы реше­ния, ~ графический метод. ~ т.д.

Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная.

Однако даже для таких задач оптималь­ное решение может быть найдено для определенного класса це­левых функций. В отличие от задач линейного программирования, где точками экстремума являются верши­ны многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине.

При решении задач нелинейного программирования для це­левой функции необходимо определить глобальный максимум или глобальный минимум.

Глобальный максимум функции - наибольшее значение из ло­кальных максимумов.

Глобальный минимум функции - наименьшее значение из ло­кальных минимумов.

Наличие локальных экстремумов затрудняет решение за­дач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найден­ный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять ло­кальный экстремум, который может существенно отличаться от глобального экстремума.

2. Графический метод решения задач нелинейного программирования.

Рассмотрим примеры решения задач нелинейного програм­мирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и не­линейном виде. Так же как и в задачах линейного программи­рования, они могут быть решены графически.

 

2.1. Задача с линейной целевой функцией и нелинейной системой ограничений

Пример 1. Найти глобальные экстремумы..

Целевая функция . Ограничения:

Решение. Область допустимых решений - часть окруж­ности с радиусом 4, которая расположена в первой четверти.

Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2.

Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем че­рез точку А прямую, перпендикулярную линии уровня.

Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение x ₂ = 1/2 х ₁.

Решение системы, очевидно:

х ₁ = 8 /5, x ₂ = 4 /5, при этом L = 16 /5 + 4 /5 = 4 .

Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4 , — в точке А (8 /5, 4 /5).

2.2. Задача с нелинейной целевой функцией и линейной системой ограничений

Пример 2. Найти глобальные экстремумы.

Целевая функция Ограничения:

 

Решение. Область допустимых решений – фигура OABD.

Линиями уровня будут окружности с центром в точке O ₁. Максимальное значение целевая функция имеет в точке D (9, 0), минимальное — в точке O ₁ (2, 3). Поэтому

Ответ. Глобальный максимум, равный 58, достигается в точке D (9, 0), глобальный минимум, равный нулю, — в точке O ₁ (2, 3).

3. Метод множителей Лагранжа

Дана задача нелинейного программирования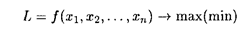

при ограничениях:

Предположим, что функции f (x ₁, х ₂ ,..., x_п) и g_i(x ₁, x ₂,..., x_п) непрерывны вместе со своими первыми частными про­изводными.

Ограничения заданы в виде уравнений, поэтому для ре­шения задачи воспользуемся методом отыскания условного эк­стремума функции нескольких переменных.

Для решения задачи составляется функция Лагранжа

где λ _i — множители Лагранжа.

Пояснения. Функция Лагранжа есть сумма целевой функции и ограничений, умноженных на множитель, который будет получен при решении системы составленной из частных производных функции Лагранжа

Затем определяются частные производные:

Приравняв к нулю частные производные, получим систему

Решая систему, получим множество точек, в которых целевая функция L может иметь экстремальные значения. Следует отметить, что условия рассмотренной системы являются необходимыми, но недостаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции. Применение метода бывает оправданным, когда заранее предполагается существование глобального экстремума, совпадающего с единственным локальным максимумом или минимумом целевой функции.

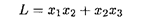
Пример 8. Найти точку условного экстремума функции

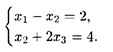
Ограничения:

Решение. Составим функцию Лагранжа:

 

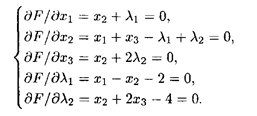Пояснения. Для составления функции Лагранжа запишем ограничения в виде: q₁=x₁-x₂-2 и q₂=x₂+2x₃-4. Функция Лагранжа есть сумма целевой функции и ограничений, умноженных на множитель, который будет получен при решении системы составленной из частных производных функции Лагранжа.

Найдем частные производные функции Лагранжа по пере­менным x ₁, x ₂, x ₃, λ₁, λ₂. Приравняв к нулю полученные вы­ражения, решим систему

λ₁ = - x ₂, λ₂ = - x ₂/2,

х ₁ = -2, x ₂ = -4, x ₃ = 4, L = -8.

Определим характер экстремума, изменяя полученные зна­чения переменных.

Измененные значения должны удовлетво­рять заданной системе ограничений.

Возьмем х ₁ > -2, напри­мер x ₁ = -1, тогда из системы ограничений получим х ₂ = -3, x ₃ = 7/2, L = -15/2.

Возьмем х ₁ < -2, например х ₁ = -3, тогда получим х ₂ = -5, x ₃ = 9/2, L = -15/2.

Следовательно, L = -8 — минимальное значение функции.

Ответ. Точка экстремума х ₁ = -2, x ₂ = -4, x ₃ = 4, максимальное значение функции L = -8.

 

Основные понятия динамического программирования

Основные понятия, идея динамического программирования.

Динамическое программирование - один из разделов оп­тимального программирования, в котором процесс принятия решения и управления может быть разбит на отдельные эта­пы (шаги).

Экономический процесс является управляемым, если мож­но влиять на ход его развития. Под управлением понимает­ся совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса.

Например, работа предприятия по выпуску продукции есть управляемый процесс.

При этом должны приниматься некоторые решения, правила в течение всего процесса работы. Совокупность ре­шений, принимаемых в начале года (квартала и т.д.) по обеспе­чению предприятия сырьем, замене оборудования, финансиро­ванию и т.д., является управлением.

Необходимо организовать выпуск продукции так, чтобы принятые решения на отдель­ных этапах способствовали получению максимально возмож­ного объема продукции или прибыли.

Динамическое программирование позволяет свести одну сложную задачу со многими переменными ко многим задачам с малым числом переменных. Это значительно сокращает объ­ем вычислений и ускоряет процесс принятия управленческого решения.

В отличие от линейного программирования, в котором сим­плексный метод является универсальным методом решения, в динамическом программировании такого универсального ме­тода не существует.

Одним из основных методов динамичес­кого программирования является метод рекуррентных соотношений, который основывается на использовании принципа оптимальности.

Принцип оптимальности состоит в том, что, каковы бы ни бы­ли начальное состояние на любом шаге и управление, выбран­ное на этом шаге, последующие управления должны выбирать­ся оптимальными относительно состояния, к которому придет система в конце данного шага.

Пример 1. Определить оптимальный цикл замены оборудо­вания при следующих исходных данных:

Р = 10, S(t) = 0,

f(t) = r(t) — u(t),

 

Решение. Уравнения (1) и (.2) запишем в следующем виде:

 

Для N = 1

Для N = 2

 

 

Вычисления продолжаем до тех пор, пока не будет выпол­нено условие f ₁(1) > f ₂(2), т.е. в данный момент оборудование необходимо заменить, так как величина прибыли, получаемая в результате замены оборудования, больше, чем в случае ис­пользования старого. Результаты расчетов помещаем в табли­цу, момент замены отмечаем звездочкой, после чего дальней­шие вычисления по строчке прекращаем (табл. 29.2).

Можно не решать каждый раз уравнение, а вычис­ления проводить в таблице. Например, вычислим f ₄ (t):

Дальнейшие расчеты для f ₄ (t) прекращаем, так как f ₄(4) = 23 < f ₃(1) = 24.

По результатам вычислений и по линии, разграничиваю­щей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года.

Ответ. Для получения максимальной прибыли от ис­пользования оборудования в двенадцатиэтажном процессе оп­тимальный цикл состоит в замене оборудования через каждые 4 года.

 

Понятие графа

Основные понятия теории графов.

Теория графов – один из универсальных и нагляд­ных языков: графический, который применяется во многих облас­тях науки и техники.

Теория графов дает исключительно удобный аппарат для моделирования структурных свойств различ­ных систем и отношений между объектами разной природы, в том числе программных моделей.

Графом G = ( W, X) называется пара двух конечных множеств: множество точек и множество линий, соединяющих некоторые пары точек

Граф - множество линий X, соединяющее пары точек множества W. Точки называются вершинами (узлами) графа, линии - ребрами графа.

Если задан граф G = ( W, X), тоW - конечное непустое множество его вершин, X – множествоего ребер.

Ребро называется инцидентным по отношению к тем вершинам, которые оно соединяет.

Две вершины графа на­зываются смежными, если существует инцидентное им ребро.

Два ребра называются смежными, если они имеют общую вершину.

Графназывается ориентированным (направленным), если он состоит из упорядоченных пар вершин (кортежи длины 2). Такой граф еще называется орграфом.

В направленном графе ребра изображаются стрелками, идущими от первой компоненты (начало ребра) кортежа ко второй (конец ребра). См рисунок.

Маршрутом называется последовательность попарно инцидентных вершин V₁, V₂,..., V_i неориентированного графа, т.е. последовательность ребер не­ориентированного графа, в которой вторая вершина предыдуще­го ребра совпадает с первой вершиной следующего.

Длиной маршрута называется число ребер этого маршрута.

Для одних и тех же вершин может оказаться несколько маршрутов разной или одинаковой длины, среди которых выбирается наиболее оптимальный маршрут, как правило – наименьший маршрут.

Маршрут принято задавать как последователь­ность ребер, поскольку это более удобно при наличии кратных ребер.

Маршрут называется замкнутым или циклом, если начальная вершина маршрута совпадает с конечной,

Расстоянием между двумя вершинами называется минималь­ная длина из всех возможных маршрутов между этими вершина­ми при условии, что существует хотя бы один такой маршрут.

Расстояние можно обозначать символами: d(A;B)= min|A;B|=k, где вершины A и B начало и конец маршрута, k – число, равное наименьшей длине маршрута.

Поскольку рассматриваются конечные графы, минимум мож­но найти всегда.

Одна из задач теории графов есть нахождение кратчайших путей в графе. На данный момент есть различные методы решения такой задачи, некоторые из которых будут рассмотрены в этом разделе.

В орграфе маршрут является ориентированным и называется путем. На путь сразу налагаются важные требования, являющиеся частью определения:

• направление каждой дуги должно совпадать с направлением пути;

• ни одно ребро пути не должно встречаться дважды.

Поэтому путь - упорядоченная последовательность ребер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны.

В графе цепь, путь и цикл называются простыми, если они проходят через любую из вершин не более одного раза.

Неориен­тированный граф называется связным, если между любыми дву­мя его вершинами есть маршрут.В противном случае он называется - несвязным.

Две вершины называются связными, если существует маршрут между ними.

Граф G можно разбить на непересекающиеся подмножества (графы)по признаку связности, которые называются подграфами.

Вершины одного множества являются связ­ными между собой, а вершины различных множеств - несвязны.

Ребро связного графа G на­зывается мостом, если после его удале­ния G станет несвязным и распадется на два связных графа G' и G".

Способы задания графа:

Графы могут задаваться следующими способами:

1. Геометрическим способом - рисунки, схемы, диаграммы,

2. Алгебраическим способом - перечислением вершин и ребер,

3. Табличным способом. 4. Матричным способом

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: