Оформлення звіту. Лабораторна робота  №5. Необхідна кількість вимірювань для досягнення заданої точності. 5. 1. Відома середня квадратична помилка вимірювань.

Оформлення звіту

1. Переписати текст вихідної інформації з наведенням вибірки, відносних похибок δ ₁ та δ ₂ приладів П1 та П2.

2. За стандартною програмою статистичних обчислень (наприклад, на калькуляторі типу СІТІZЕN) обчислити m_х=х та S_х=σ _n-1.

3. За пунктом 2 виключити грубі помилки і скорегувати нові значення вибіркової середньої m_х стандарту вибірки та її об’єму n.

4. За пунктами 3-5 з наведенням відповідних формул обчислити значення ε, Θ та Δ.

5. Результати обчислень оформити в таблицю

mх	n	Sх	ε	Θ 1	Θ 2	Θ	Δ

Межі інтервалів

mх-ε	mх+ε	mх-Θ	mх+Θ	mх-Δ	mх+Δ

6. Обчислити значення

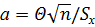                                                                                      (4. 10)

порівняти значення ε, Θ та Δ і зробити висновок, що більшим чином ε (а 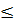0, 8) чи Θ (а 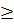8) впливає на результуючу величину Δ.

Контрольні запитання

1. Відносна та абсолютна похибки та їх взаємозв’язок.

2. Що таке випадкова похибка і чим вона викликана?

3. Систематичні похибки і причини їх виникнення.

4. Які похибки неможливо виключити ні за яких умов?

5. Охарактеризувати послідовність статистичної обробки результатів вимірювання.

ЛАБОРАТОРНА РОБОТА  №5

Необхідна кількість вимірювань для досягнення заданої точності

Мета роботи: Навчитись планувати кількість необхідних вимірів в залежності від заданої випадкової похибки та класу точності засобів вимірювань.

5. 1. Відома середня квадратична помилка вимірювань.

Збільшуючи кількість вимірювань N навіть при їхній точності, можна збільшити надійність довірчих оцінок або звузити довірчий інтервал для істинного значення вимірювальної величини. Необхідна кількість вимірювань для досягнення необхідної точності ε та необхідної надійності t можна визначити заздалегідь лише у тому випадку, коли відома середня квадратична помилка вимірювань (виміри припускаються рівно точними і незалежними). У цьому випадку кількість вимірювань N для одержання довірчої оцінки точності ε:

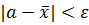,                                                                           (5. 1)

З заданою надійністю £ визначається за допомогою формули:

,                                                                      (5. 2)

де t =t(Р) знаходиться з рівності 2Ф(t) = Р з табл. 5. 1. (далі розглядається приклад №1 розрахунків).

5. 2. Невідома середня квадратична помилка вимірювань.

Якщо середня квадратична помилка вимірювань заздалегідь невідома, але відомий хоча б її порядок, тоді необхідну кількість вимірювань можна визначити в залежності від надійності Р і від відношення q = ε /s, де s – майбутній емпіричний стандарт помилки. Для визначення N в залежності від Р і q застосовується табл. 5. 2. (далі розглядається приклад №2 розрахунків).

ПРИКЛАД: щоб гарантувати одержання довірчої оцінки з надійністю Р = 0, 99 та точністю до 0, 1s слід зробити 668 вимірювань. На практиці часто можна обмежитися меншим числом вимірювань, якщо застосовувати наступний прийом. Спочатку потрібно зробити порівняно невелику кількість вимірів ( у 3-4 рази менш означеного у таблиці 5. 2). По результатах цих вимірювань розрахувати довірчий інтервал. Після цього уточнити необхідну кількість вимірів, виходячи з того, що зменшення довірчого інтервалу в λ – раз збільшує кількість замірів у 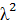 разів (наприклад, зменшення довірчого інтервалу у 2 рази забезпечується збільшенням кількості вимірів у 4 рази).

Таблиця 5. 1.

Величини, пов’язані із інтегралом ймовірності Ф(t);

1 -Р	t =t(Р)	Р
0. 05	1. 960	0. 95
0. 04	2. 054	0. 96
0. 03	2. 170	0. 97
0. 02	2. 326	0. 98
0. 01	2. 576	0. 99
0. 009	2. 612	0. 991
0. 008	2. 652	0. 992
0. 007	2. 697	0. 993
0. 006	2. 748	0. 994
0. 005	2. 807	0. 995
0. 004	2. 878	0. 996
0. 003	2. 968	0. 997
0. 002	3. 090	0. 998
0. 001	3. 291	0. 999
0. 0009	3. 320	0. 9991
0. 0008	3. 353	0. 9992
0. 0007	3. 390	0. 9993
0. 0006	3. 432	0. 9994
0. 0005	3. 481	0. 9995
0. 0004	3. 540	0. 9996
0. 0003	3. 615	0. 9997
0. 0002	3. 720	0. 9998
0. 0001	3. 891	0. 9999

Функція t =t(Р) є зворотною для Р =2Ф(t)

t	Ф(t)	1-2Ф(t)
2. 5	0. 49379	0. 01242
2. 6	0. 49534	0. 00932
2. 7	0. 49653	0. 00693
2. 8	0. 49744	0. 00511
2. 9	0. 49813	0. 00373
3. 0	0. 49865	0. 00270
3. 1	0. 49903	0. 00194
3. 2	0. 49931	0. 00137
3. 3	0. 49952	0. 00097
3. 4	0. 49966	0. 00067
3. 5	0. 499767	0. 000465
3. 6	0. 499841	0. 000318
3. 7	0. 499892	0. 000216
3. 8	0. 499927	0. 000145
3. 9	0. 499952	0. 000096
4. 0	0. 499968	0. 000063
4. 1	0. 499979	0. 000041
4. 2	0. 499987	0. 000027
4. 3	0. 499991	0. 000017
4. 4	0. 499995	0. 000011

 

 

Таблиця 5. 2.

Розрахунок необхідної кількості вимірювань

q = ε /s	Р
	0, 90	0, 95*	0, 98	0, 99	0, 999
1, 0
0, 5
0, 4
0, 3
0, 2
0, 1
0, 05

 

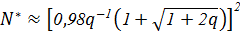, для Р =0, 95         (5. 3. )

Приклад №1. Відома середня квадратична помилка вимірювань.

Знайдемо кількість вимірювань N для одержання довірчої оцінки заданої нами точності ε = 0, 003 з прийнятою надійністю Р = 0, 95 при середньому квадратичному відхиленні вимірювань .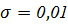

Для P = 0, 95 по табл. 5. 1 – 2 знаходимо значення t через зворотну функцію t =t(P), t =1, 96.

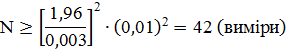
Для порівняння.

Зменшимо значення точності ε = 0, 005 при тих самих вимогах до Р = 0, 95 та .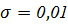

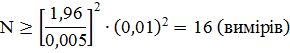
⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: