 |
Задание 3. Таблица 1. Таблица 2 . Редактор формул
|
|
|
|
Задание 3
Создайте нижеприведенные таблицы и заполните все пустые клетки в соответствии с ее содержанием.
Таблица 1

Таблица 2

Таблица 3

Таблица 4

Таблица 5


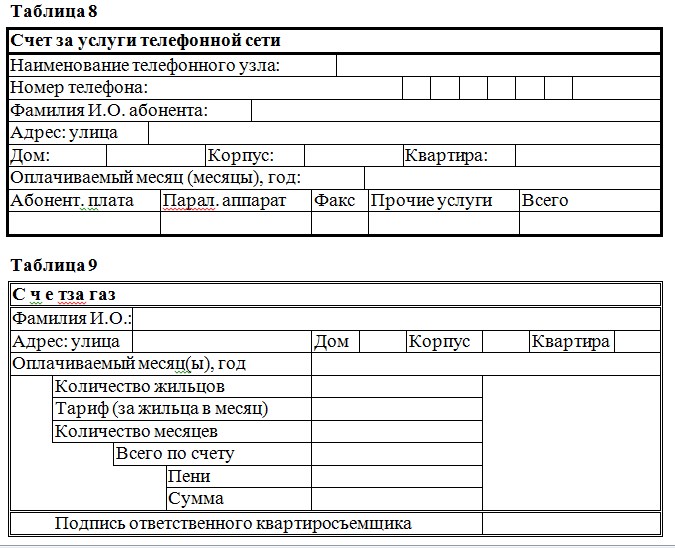
Редактор формул
Текст документа (учебного пособия, научной статьи и т. д. ) может содержать математические формулы. Для работы с формулами в текстовом редакторе Word существует «Редактор формул». Открывается Редактор формул командами: «Вставка\Уравнение». В документе появится окно Редактора формул (рис. 1. 11).
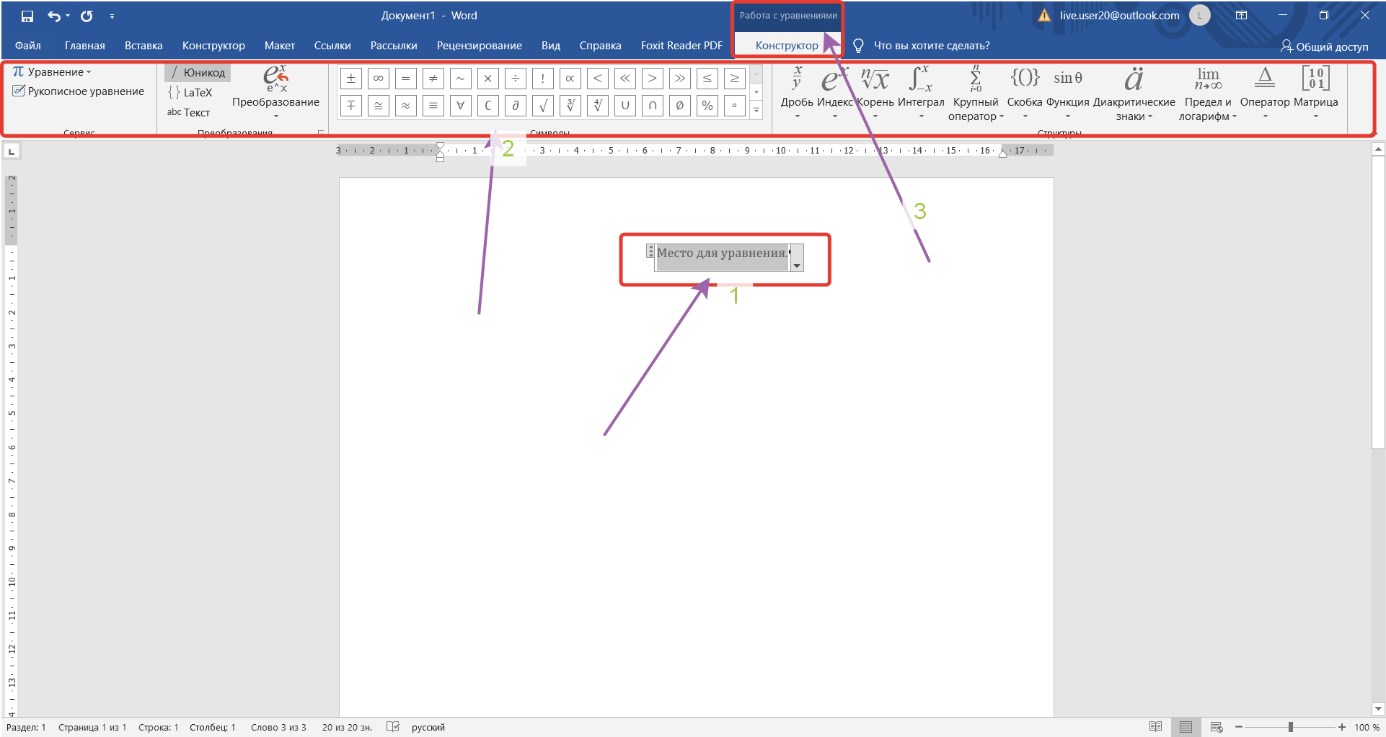
Рис. 1. 11 Окно Редактора формул
Как видно из рисунка 11, окно Редактора формул состоит из трех частей:
– место для уравнения или ввода формулы (см. область, обозначенную на рисунке 1. 11 цифрой 1);
– галерея формул, содержащая несколько известных формул, открывается щелчком правой кнопки мыши на треугольник, расположенный справа от команды
« 𝜋 Уравнение∵ » \Вставка\Символы » (см. на рис. 1. 11 цифру
2);
– контекстная вкладка «Конструктор», расположенная на ленте (см. цифру 3).
Набор формулы осуществляется в «Место для формулы», используя контекстную вкладку «Конструктор» и «Галерею формул». При этом редактирование формулы производится теми же методами, что и редактирование текста.
Формула представляется в двух форматах: линейном и профессиональном. Переход от линейного вида к профессиональному и наоборот осуществляется путем нажатия левой клавишей мыши на треугольнике в правой части «Место для формулы». На экране появится контекстное меню, где можно произвести соответствующий переход. Для примера создадим формулу:

и вставим эту формулу в «Галерею формул».
|
|
|
1). Устанавливаем курсор в позицию, в которую хотим вставить формулу.
2). На ленте набираем «Вставка\Уравнение». В документе появляется окно Редактора формул рис. 1. 11.
3). В «Место для уравнения», используя контекстную вкладку «Конструктор», «Галерею формул» и клавиатуру, вводим формулу
 .
.
Сохраним созданную формулу в галерее формул, чтобы в дальнейшем при необходимости ее можно было быстро вставлять в документ. Для этого:
а) щелкаем левой клавишей мыши на треугольнике в правой части поля формулы, чтобы открыть контекстное меню;
б) в появившемся контекстном меню выбираем команду «Сохранить как новую формулу». На экране появится диалоговое окно «Создание нового стандартного блока» (рис.
1. 12);
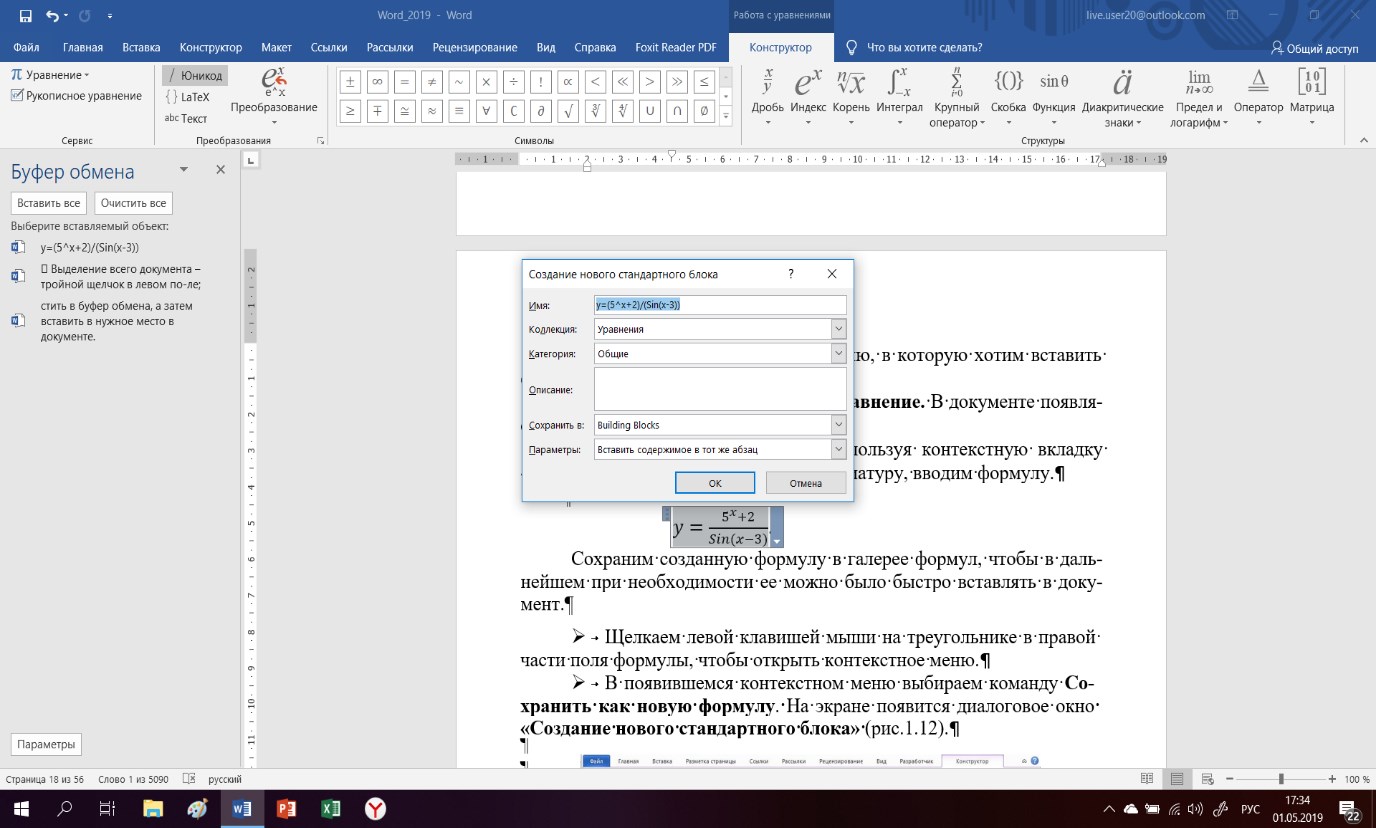
Рис. 1. 12 Диалоговое окно «Создание нового стандартного блока»
в) в поле Имя вводим имя сохраняемой формулы. Это может быть любое имя, например, Моя первая формула.
г) нажимаем кнопку ОК, окно будет закрыто, и формула помещена в галерею формул.
Убеждаемся в том, что созданная формула помещена в галерею формул.
Задание 4
В MS Word с помощью редактора формул создать выражения в соответствии с заданным вариантом 0–9, определяемым по последней цифре номера зачетной книги студента.
Вариант 0:
Вычислить значения функции 𝑦:
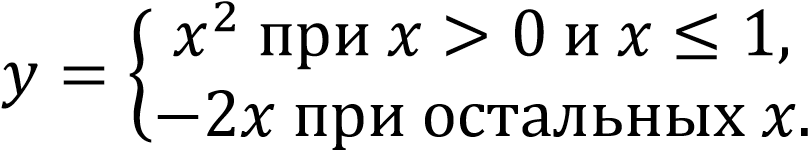 .
.
Вариант 1:
Вычислить значения функции 𝑦:
𝑒 2𝑥 при 𝑥 > 1 и 𝑥 ≤ 0,
𝑦 = { 3𝑥 при 𝑥 > 0 и 𝑥 < 0, 5, .
ln (2 + 𝑥 ) при остальных 𝑥.
Вариант 2:
Вычислить значения функции 𝑦:
 .
.
Вариант 3:
Создать таблицу значений функции двух переменных 𝑥, 𝑦
 .
.
𝑥, 𝑦 меняются в пределах от 0 до 90 градусов с шагом 10 градусов.
Вариант 4:
Создать таблицу значений функции двух переменных 𝑥, 𝑦
 .
.
𝑥, 𝑦 меняются в пределах от 0 до 30 градусов с шагом 5 градусов.
Вариант 5:
|
|
|
Проверить тождество:
 .
.
при 𝑛 = 2, 5, 6
Вариант 6:
Проверить тождество:
 .
.
при 𝑛 = 3, 4, 7
Вариант 7:
Решить методом обратной матрицы систему линейных уравнений:
2𝑥 + 3𝑦 − 𝑧 = 3, { 3𝑥 − 3𝑦 + 𝑧 = 2, .
2𝑥 − 3𝑦 − 𝑧 = − 3.
Вариант 8:
Решить методом Крамера систему линейных уравнений: 2𝑥 + 3𝑦 − 𝑧 = 3, { 3𝑥 − 3𝑦 + 𝑧 = 2, .
2𝑥 − 3𝑦 − 𝑧 = − 3.
Вариант 9:
Найти матрицу, обратную к матрице:
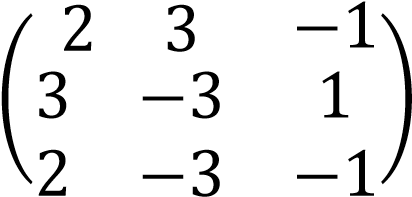 .
.
Набрать следующие формулы Вариант 10, Вариант 11: Вариант 10:

Вариант 11:

|
|
|


