 |
1.2 Аэродинамическая компоновка вертолета и характеристики основных частей вертолета Ми-8Т(МТ)
|
|
|
|
1. 2 Аэродинамическая компоновка вертолета и характеристики основных частей вертолета Ми-8Т(МТ)
Под аэродинамической компоновкой вертолета понимается выбор внешних форм и способов сочетания частей вертолета, которые создают в полете основные аэродинамические силы и моменты.
Применительно к вертолету Ми-8 аэродинамическая компоновка характеризуется:
- расположением несущего и рулевого винтов;
- формами (обводами) фюзеляжа;
- типом и расположением силовой установки;
- наличием, расположением и формами стабилизатора и киля;
- типом и расположением взлетно-посадочных устройств;
- количеством и формами выступающих в поток элементов (внешних подвесок, спец. ферм и т. д. ).
Каждая из перечисленных частей вертолета имеет определенные аэродинамические характеристики. Будучи объединенными в той или иной компоновке, эти части оказывают взаимное влияние на аэродинамические характеристики друг друга (аэродинамическая интерференция). Поэтому аэродинамические характеристики вертолета в целом отличаются от суммы аэродинамических характеристик изолированно рассматриваемых частей.
Примерами такого взаимного влияния являются: несущий винт и фюзеляж, фюзеляж и стабилизатор, рулевой винт и киль и т. д.
Вертолет Ми-8Т(МТ) создан по классической одновинтовой схеме с рулевым винтом, с механическим приводом несущего винта.
1. 2. 1 Несущий винт
Несущий винт, создавая силу тяги – ТНВ, обеспечивает получение подъемной силы – ТYa и пропульсивной силы – ТXa, необходимых для выполнения заданного режима полета или маневра. Обеспечивает продольное и поперечное управление вертолетом.
Несущий винт вертолета Ми-8Т(МТ) состоит из 5 лопастей и втулки. Лопасть имеет прессованный дюралюминиевый лонжерон, к которому крепятся наконечник лопасти, 21 хвостовой отсек и концевой обтекатель. Втулка имеет горизонтальные, вертикальные и осевые шарниры. Вертикальные шарниры имеют гидравлические демпферы. Втулка также имеет регулятор (компенсатор) взмаха, который обеспечивает изменение установочного угла лопасти при ее взмахе (K=0, 5).
|
|
|
Основные геометрические и аэродинамические характеристики несущего винта
| Модификации вертолета | МИ – 8Т | МИ – 8МТ |
| Диаметр, м | 21, 294 | 21, 294 |
| Число лопастей | ||
| Площадь, ометаемая несущим винтом, м² | 355, 9 | 356, 1 |
| Коэффициент заполнения | 0, 0777 | 0, 0777 |
| Угол свеса лопастей: по нижнему упору: по центробежному ограничителю |
4º 
1о40´ +20´
|
4º
1о40´ +20´
|
| Максимально возможный угол взмаха | 25°±3° | 25°±3° |
| Угол установки лопастей r =0, 7: минимальный максимальный | 2о40´ 15о | |
| по указателю УШВ: минимальный максимальный | 1о±10´ 14о±30´ | |
| Коэффициент компенсации взмаха | 0, 5 | 0, 5 |
| Угол отклонения лопасти в плоскости вращения: вперед назад | 13о±15´ 11о±10´ | 13о±15´ 11о±10´ |
| Угол наклона оси несущего винта вперед | 4о30´ -10´ | 4о30´ -10´ |
| Угол наклона автомата перекоса: вперед назад влево вправо |
7о  
5о 
4о12´ ±12´
3о24´ ±12´
|
7о
5о
4о12´ ±12´
3о24´ ±12´
|
| Частота вращения несущего винта nнв | 192 об/мин | 192 об/мин |
| Окружная скорость конца лопасти ω R | 213, 26 м/сек | 213, 26 м/сек |
| Удельная нагрузка на ометаемую несущим винтом площадь | G=11100 кгс – P=31 кгс/м2 G=12000 кгс – P=34кгс/м2 G=13000 кгс – Р=36, 4 кгс/м2 | |
| Лопасть прямоугольной формы в плане с хордой | b=0, 52 м | b=0, 52 м |
| Разнос горизонтальных шарниров | 220 мм | 220 мм |
| Разнос вертикальных шарниров | 507 мм | 507 мм |
| Вес лопасти | 140 кгс | 140 кгс |
| Вес комплекта лопастей | 700 кгс | 700 кгс |
| Вес втулки несущего винта | 610, 5 кгс | 610, 5 кгс |
| Общий вес несущего винта | 1310, 5 кгс | 1310, 5 кгс |
| Профиль лопасти 1 – 2 отсеки 4 – 21 отсеки 3 отсек | NACA-230 NACA-230M переходный | NACA-230 NACA-230М переходный |
| Максимальное аэродинамическое качество несущего винта: K | 9 – 10 | |
Лопасти НВ имеют геометрическую и аэродинамическую крутку (Рис. 1). Под геометрической круткой подразумевается изменение углов установки сечений по радиусу лопасти на угол Δ φ. У вертолета Ми-8 лопасть имеет геометрическую крутку Δ φ = 5°. На участке от сечения №1 до сечения №4 Δ φ = 0°. Далее крутка изменяется по линейному закону и равна –5о на конце лопасти в сечении №22.
|
|
|
Геометрическая крутка лопасти выполняется с целью:
- более равномерного распределения аэродинамической нагрузки по длине лопасти;
- получения прироста тяги несущего винта;
- уменьшения потребной мощности для вращения винта;
- увеличения максимальной скорости полета вертолета.
Металлическая конструкция лопасти позволяет точно выдержать теоретический контур профиля.
Лопасть имеет триммер, представляющий собой дюралюминовую пластинку, выступающую за пределы задней кромки лопасти. Триммер служит для изменения моментных характеристик лопасти. Кроме того, триммер используется при регулировании соконусности лопастей несущего винта.
Рис. 1 Форма лопасти в плане. Аэродинамическая и геометрическая крутка
Под аэродинамической круткой понимается конструктивное изменение профилей элементов лопасти по форме, толщине и кривизне. У лопастей вертолета Ми-8Т(МТ) относительная толщина профилей от корня до конца лопасти уменьшается от 13% до 11, 38% по ступенчатому закону. Уменьшение толщины лопасти к ее концу улучшает аэродинамические свойства винта в целом за счет увеличения критической скорости и числа Мкр концевых частей лопасти. Это в свою очередь снижает потребный крутящий момент несущего винта по причине уменьшения волнового сопротивления. В комле 
=13%. От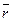 
=0, 230 до 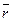=0, 2676 =12%. От 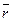=0, 3051 до конца лопасти =11, 38%.
|
|
|
Изменения относительной толщины профиля и углов геометрической крутки лопасти выбраны из условий получения высокого аэродинамического качества несущего винта и обеспечения динамической прочности лопасти.
Важной составной частью аэродинамических характеристик вертолета являются аэродинамические характеристики несущего винта. Основой для определения аэродинамических характеристик винта являются аэродинамические характеристики профилей лопастей (рисунок 2, 3).
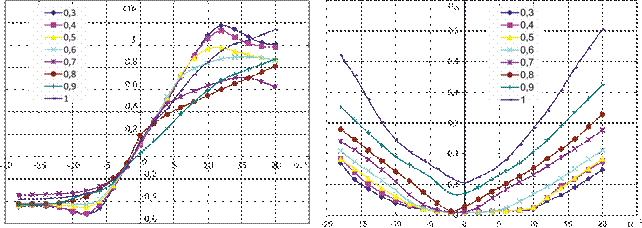
Рис. 2 Зависимость коэффициента подъемной силы и профиля коэффициента силы лобового сопротивления NACA230-12 от углов атаки и чисел М
Рис. 3 Зависимость коэффициента продольного момента профиля NACA230-12 от углов атаки и чисел М и семейство поляр профиля NACA230-12
Способность НВ создавать тягу определяется, в основном, аэродинамическими характеристиками профилей лопастей, из которых они набраны, их геометрической круткой, коэффициентом заполнения и условиями работы несущего винта.
Проводя рассуждения на примере работы элемента лопасти (Рис. 4), покажем, как на несущем винте формируются тяга и момент сопротивления вращению.
Выделенные элементы на радиусе r будут ометать кольцевую площадку шириной ∆ r, прогоняя через нее воздух со скоростью v1 и образуя элементарную кольцевую струю. При этом они создают некоторую тягу ∆ Т, а для их вращения потребуется преодолевать сопротивление воздуха в плоскости вращения ∆ Xпв.
Чтобы определить величины ∆ Т и ∆ Хпв, необходимо знать скорость обтекания и угол атаки элемента aэ. С этой целью построим треугольник скоростей (Рис. 4).
Рис. 4 К вопросу формирования на несущем винте вертолета силы тяги и момента сопротивления
Элемент, имеющий угол установки 
, движется относительно воздуха со скоростью Wэ, которая получается векторным сложением окружной скорости ω нr и индуктивной скорости подсасывания ν 1, и истинным углом атаки aэ. Чтобы его найти, воспользуемся допущением. Так как величина v1 по сравнению с ω нr мала, то и угол притекания β э (угол между вектором скорости Wэ и плоскостью вращения) мал. Можно принять, что:
|
|
|
.
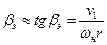По этой же причине можно принять Wэ = ω нr. Тогда истинный угол атаки элемента лопасти:
.
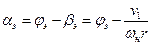То есть определение истинных углов атаки элементов при известных углах установки jэ сводится к определению величины индуктивной скорости для каждого элемента лопасти. Как в импульсной теории, так и в теории элемента лопасти определение v1 – основная и сложная задача, которая решается либо экспериментальным, либо расчетным путем.
Зная распределение истинных углов атаки aэ по длине лопасти и числа 
для каждого элемента, можно воспользоваться характеристиками профиля (Рис. 2) с целью определения Суа = f(a, М) и Сха=f (a, М). Далее по формулам (1. 1) определяем истинную подъемную силу ∆ Yаэ и силу профильного, т. е. безындуктивного, сопротивления элемента ∆ Хаэ:
. (1. 1)
Построим аэродинамические силы ∆ Yaэ и ∆ Xaэ, действующие на данный элемент, используя скоростную систему координат. По ним определяем полную аэродинамическую силу элемента ∆ Rэ.
Проекция полной аэродинамической силы элемента ∆ Rэ на ось вала называется силой тяги элемента ∆ Тэ, а проекция ее на плоскость вращения – силой сопротивления вращению элемента ∆ Хэ пв.
,
.
Ввиду малости угла β э можно считать sin β э 
β э и cos β э 1, а величиной ∆ Xaэsin β э можно пренебречь, т. к. она очень мала по сравнению с величиной ∆ Yaэcos β э. Тогда:
, (1. 2)
. (1. 3)
В выражении (1. 3) первое слагаемое представляет собой индуктивное сопротивление, т. е. результат скоса потока, возникающего вследствие наличия индуктивной скорости v1, второе – профильное сопротивление, являющееся суммой сопротивления трения и сопротивления давления формы.
Переходя к бесконечно малым размерам элемента, формулу 1. 2 перепишем в виде:
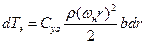, (1. 4)
а формулу 1. 3 в виде:
. (1. 5)
При осевом обтекании тяга лопасти не зависит от ее азимутального положения. Поэтому для k – лопастного винта сила тяги несущего винта равна
(1. 6)
Результат интегрирования можно представить в виде:
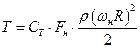, (1. 7)
где 
– коэффициент силы тяги винта; 
– коэффициент подъемной силы характерного сечения лопасти так как aэ неодинаковы по длине лопасти; 
– коэффициент заполнения несущего винта.
Для k-лопастного винта при осевом обтекании момент сопротивления вращению винта равен:
|
|
|
. (1. 8)
В результате интегрирования получим:
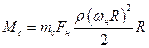, (1. 9)
где mc – коэффициент момента сопротивления вращению винта, который равен сумме коэффициентов профильного и индуктивного сопротивлений mc = mc пр + mc инд.
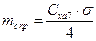– коэффициент момента сопротивления от силы профильного сопротивления;
– коэффициент момента сопротивления от силы индуктивного сопротивления.
В первом приближении, как и при расчете тяги, можно ограничиться средними значениями Сха и Суа, приняв их равными Сха7 и Суа7 соответственно. Расчет угла атаки в этом сечении находится по величине (v1)7
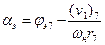(1. 10)
Коэффициент тяги Ст и коэффициент крутящего момента mкр определяем из семейства поляр несущего винта (рис. 1. 8, 1. 9) для режимов осевого и косого обтекания. Далее по формулам 1. 7…1. 9 определяем силу тяги несущего винта и момент сопротивления вращению, который при постоянных оборотах несущего винта равен моменту крутящему.
Рис. 5 Поляра несущего винта вертолета Ми-8(осевой режим)
Переход от крутящего момента к мощности, потребной для вращения несущего винта, происходит по формуле:
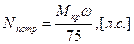или
(1. 11)
Теперь условия работы отдельных элементов лопасти остаются как бы за кадром, а вычисление таких жизненно важных характеристик НВ как его тяга и мощность, потребная для вращения НВ на различных режимах его работы, осуществляется достаточно просто, по формулам (1. 7) и (1. 11).
Входящие в эти формулы коэффициент тяги Ст и коэффициент крутящего момента mкр являются собственными характеристиками НВ и определяют его несущую способность и качество. Эти коэффициенты зависят от угла установки лопастей НВ jош (общего шага НВ), частоты вращения nнв (оборотов НВ) и режима полета m (коэффициента режима работы НВ)
(1. 12)
Из поляр (рис. 1. 5, 1. 6, 1. 11) видно, что при увеличении общего шага и тяга, и потребная мощность на вращение НВ увеличиваются, при постоянном значении оборотов и скорости полета. При уменьшении оборотов (jош = const, V = const) коэффициент крутящего момента уменьшается более интенсивно, чем растет коэффициент тяги. Уменьшение частоты вращения (nнв), несмотря на некоторое увеличение Ст, приводит к падению тяги НВ, так как она в большей степени зависит от изменения оборотов НВ (1. 11). Потребная мощность на вращение НВ в этом случае уменьшается как по причине уменьшения mкр, так и вследствие падения оборотов НВ. На практике это явление приводит к снижению вертолета, если летчик при неизменном значении общего шага уменьшит обороты НВ, или они уменьшатся по каким-то другим причинам. При увеличении скорости полета коэффициент тяги уменьшается, а коэффициент крутящего момента растет (рис. 1. 7). Чем больше скорость полета, тем существеннее эти изменения.
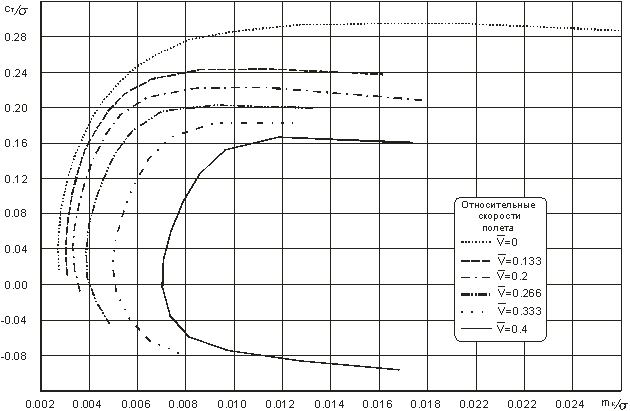
Рис. 6 Поляра несущего винта вертолета (режим косого обтекания)
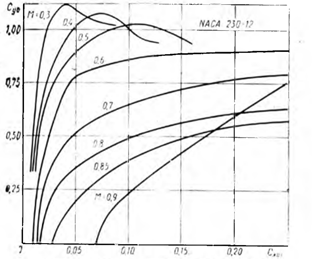
Так, на вертолете Ми-8Т(МТ) лопасть скомпонована из профилей NACA 230 и NACA 230М. Если рассмотреть зависимость Суа от α для профилей NACA230М на различных числах М, можно заметить, что для профиля NACA 230 при М < 0, 5 на малых углах атаки (до 11°) Суа изменяется лишь с изменением углов атаки. Это происходит потому, что не проявляется сжимаемость.
На больших углах атаки Суа уменьшается при увеличении числа М. Чем больше М, тем на меньшем угле атаки наступает срыв потока. У профиля NACA 230 (рис. 7) срыв потока наступает при числе М = 0, 3 на угле атаки, равном 15°. Для профиля NACA 230М величина Суа на тех же углах атаки несколько меньше при одинаковых числах М. При М до 0, 3 срыв потока наступает на больших углах атаки ( α > 15°). У этого профиля на большем диапазоне углов атаки Суа увеличивается с ростом числа М.
|
|
|
