 |
Вертикальные углы (определение). Свойства вертикальных углов
|
|
|
|
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого
3. Задача по теме "Отрезок. Измерение отрезков ".
На отрезке OD, длина которого 24 см, отмечена точка A. Найдите длину отрезка AD, если отрезок OA на 8 см длиннее отрезка AD.
Билет № 18
Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства прямоугольного треугольника (без доказательства)
Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами прямоугольного треугольника, а сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.
1. Сумма острых углов равна 90
2. Катет лежащий против угла 30 равен половине гипотенузы
3. Обратная теорема: Если катет равен половине гипотенузы, то угол, лежащий против него равен 30
Построение угла, равному данному.
Отложить от данного луча угол, равный данному.
Решение. Данный угол с вершиной А и луч ОМ
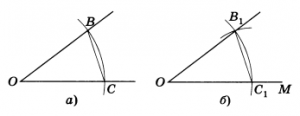
Проведем произвольную окружность с центром в вершине О данного угла. Пусть В и С — точки пересечения окружности со сторонами угла (рис а). Радиусом ОВ проведем окружность с центром в точке О — начальной точке данного луча (рис. б). Точку пересечения этой окружности с данным лучом обозначим С1. Опишем окружность с центром С1 и радиусом ВС. Точка В1 пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ОBC = Δ ОВ1С1(третий признак равенства треугольников).
2. Задача по теме "Внутренние и внешние углы треугольника ".
Один из внешних углов прямоугольного треугольника равен 130º. Найдите острые углы треугольника
|
|
|
Билет № 19
Отрезок (определение). Длина отрезка. Основное свойство измерения отрезков.
Отрезок - это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину
Расстоянием между двумя точками называется длина отрезка .
1.Каждый отрезок имеет определенную длину, большую нуля.
2.Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой.
3.При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.
4.Два отрезка называются равными, если равны их длины.
Теорема о соотношении между сторонами и углами треугольника.
Теорема
В треугольнике:
1) против большей стороны лежит больший угол;
Против большего угла лежит большая сторона.
1) Дано: ∆ ABC, AC>AB.
Доказать: ∠B>∠C.
Доказательство:
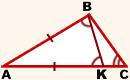Отложим на стороне AC отрезок AK: AK=AB.
Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.
Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.
Значит, у него углы при основании равны: ∠ABK=∠AKB.
Для треугольника BCK ∠AKB — внешний.
Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.
Имеем:
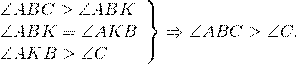
2) Дано: ∆ ABC,
∠B>∠C.
Доказать: AC>AB.
Доказательство:
(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо AC<AB.Если AC=AB, то треугольник ABC — равнобедренный с основанием BC и у него углы при основании равны: ∠B=∠C, что противоречит условию.По доказанному в пункте 1), против большей стороны лежит больший угол. Поэтому, если AC<AB, то ∠B<∠C. Снова пришли к противоречию.Значит, выдвинутое нами предположение неверно. Следовательно, AC>AB.
Что и требовалось доказать.
3. Задача по теме "Виды треугольников ".
Периметр равностороннего треугольника DEK равен 18 см. Найдите стороны треугольника DEK.
|
|
|
Билет № 20
Угол (определение). Развернутый угол. Внутренняя и внешняя область угла.
|
|
|
