 |
Оптимизация режимов токарной обработки
|
|
|
|
Методические указания к выполнению практических работ по дисциплине
«Оптимизация технологических процессов»
Методические указания
Волгоград
УДК 006
Рецензент:
к.т.н., доцент А. В. Авилов
Издаётся по решению редакционно-издательского совета
Волгоградского государственного технического университета
Соломоненко, С.А. Методические указания к выполнению практических работ по дисциплине «Оптимизация технологических процессов» [Электронный ресурс]: методические указания / С.А. Соломоненко // Сборник «Методические указания» Выпуск 3. – Электрон. текстовые дан. (1 файл: 258.5 Кb). – Волгоград: ВПИ (филиал) ВолгГТУ, 2012. – систем. требования: Windows 95 и выше; ПК с процессором 486+; CD-ROM.
Содержит сведения по оптимизации режимов резания. Рассматриваются вопросы по выбору критериев оптимизации и ограничений. Рассчитано на студентов всех форм обучения машиностроительных специальностей.
Содержит варианты заданий для выполнения практических работ по дисциплине «Оптимизация технологических процессов». CD-ROM.
© Волгоградский государственный
технический университет, 2012
© Волжский
политехнический институт, 2012
Содержание
Введение …………………………………………………………………………4
1. Практическая работа №1 ……………………………………………..…..….5
2. Практическая работа №2……………………………………………...……...11
3. Практическая работа №3……………………………………………..............25
4. Практическая работа №4……………………………………….…..………...28
Список рекомендуемой литературы……………………………........................36
|
|
|
Введение
В настоящей работе уделяется внимание методам решения классических оптимизационных задач, возникающих при технологическом проектировании машиностроительного производства, связанного с обработкой деталей машин.
Назначение параметров резания должно находиться во взаимосвязи с их влиянием на работоспособность инструмента. Однако форсирование режима резания, необходимое для повышения производительности и снижения себестоимости обработки, как правило, оказывает негативное влияние на ресурс инструмента и стабильность его работы во времени. Поэтому управление процессом резания как задача выбора его параметров направлено на поиск компромиссного решения, удовлетворяющего противоречивым требованиям, и прежде всего требованиям стабильного протекания процесса.
Практическая работа №1
Оптимизация режимов токарной обработки
Оптимизация технологических процессов и режимов резания, в частности, основывается на построении математических моделей. Для установления математической модели выделяют технические ограничения, которые в наибольшей степени определяют описываемый процесс и оценочную функцию (критерий оптимальности).
Выбор тех или иных технических ограничений зависит от вида обработки и определяется конкретными условиями технологического, конструкционного и организационно-производственного характера. Однако можно выделить ряд наиболее важных технических ограничений, которые составляют основу математических моделей процесса резания при точении, фрезеровании, сверлении и других методах обработки. Такими ограничениями являются режущие возможности инструмента, определяемые его стойкостью; мощность электродвигателя привода главного движения; наименьшая и наибольшая скорости резания (частота вращения шпин.геля) и подача, допускаемые кинематикой станка; прочность и жесткость режущего инструмента; точность обработки; шероховатость обработанной поверхности.
|
|
|
В качестве оценочной функции при оптимизации по двум параметрам 
обычно используют минимальную себестоимость
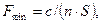(1)
где 
- коэффициент, не зависящий от режимов резания 
.
Из этого выражения видно, что функция 
будет наименьшей, когда произведение 
будет максимальным.
Технические ограничения строятся на основе известных зависимостей. Так, техническое ограничение по стойкости инструмента для точения будет получено из выражений для скорости резания:
(2)
где Т- период стойкости инструмента, мин;
- показатель относительной стойкости;
- глубина резания, мм;
- диаметр заготовки, мм;
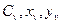- коэффициенты, характеризующие условия обработки;
- общий поправочный коэффициент.
После несложных преобразований получим техническое ограничение в следующем виде:
(3)
Аналогично определяют и другие технические ограничения. Для выбора оптимальных значений режимов резания с использованием методов линейного программирования все технические ограничения и оценочная функция приводятся к линейному виду логарифмированием. Так, выражение (2.3) после логарифмирования будет иметь вид:
(4)
Введем обозначения
(В обозначении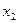 
подача 
умножается на 100, чтобы избежать получения отрицательных значений логарифмов) и получим первое техническое ограничение в линейном виде:
(5)
Для оценочной функции, с учетом ее вида (2.1) после логарифмирования будем иметь
(6)
Приведение всех технических ограничений к линейному виду и представление их в виде системы неравенств в совокупности с оценочной функцией дает математическую модель процесса резания металлов. Определение оптимальных режимов резания с помощью построенной математической модели может выполняться аналитическим или графическим методом.
Рассмотрим это на примере.
Построить математическую модель процесса резания и определить оптимальные режимы резания для точения поверхности заготовки типа вал диаметром 
100 мм и длиной 
= 700 мм, материал - сталь 45, требуемая шероховатость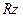 
=40 мкм, глубина резания =2,5 мм.
Решение. Учитывая размеры заготовки для обработки, выбирают токарно-винторезный станок с ЧПУ 16К20ФЗ. Точение производят проходным резцом с режущей пластиной Т15К6 с охлаждением. Размеры державки резца принимаются 
=12 мм, 
=16 мм, вылет резца 
= 50 мм. Выделим наиболее важные ограничения.
|
|
|
Ограничение 1. Режущие возможности инструмента, определяемые периодом стойкости.
Согласно зависимости (2.3) находим значения периода стойкости инструмента и коэффициентов, входящих в уравнение для 
) [16]:
.
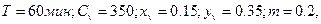
Тогда
или 
(7)
Приведем полученное неравенство к линейному виду логарифмированием, и после обозначения получим
где 
(8)
Ограничение 2. Мощность электродвигателя привода главного движения станка.
Это ограничение выражается условием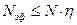 
, где 
- мощность электродвигателя главного привода станка, кВт;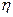 
- КПД кинематической цепи от электродвигателя к инструменту.
Эффективная мощность, кВт, затрачиваемая на процесс резания,
(9)
где 
- сила резания, которая согласно [16] определится как
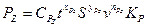. (10)
Подставляя в выражение (2.9) значение составляющей силы резания , получим для второго технического ограничения
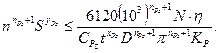(11)
Значение коэффициентов для рассматриваемого примера [16]:
Мощность электродвигателя для станка 16К20ФЗ =10 кВт, 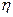= 0,85. Тогда
(12)
После приведения к линейному виду и введения обозначений получим
где 
(13)
Ограничение 3. Наименьшая допустимая скорость резания, определяемая кинематикой станка.
Для частоты вращения шпинделя станка п это ограничение имеет вид 
. Для станка 16К20ФЗ лст 
= 12,5 мин-1. Тогда 
, где 
.
Ограничение 4. Наибольшая допустимая скорость резания, определяемая кинематикой станка.
Для частоты вращения шпинделя станка это ограничение имеет вид 
. Для станка 16К20ФЗ 
= 2000 мин-1. Тогда 
, где 
.
 |
При аналогичных преобразованиях были получены в линейном виде последующие ограничения: ограничение 5 - по наименьшей подаче; ограничение 6 - по наибольшей подаче; ограничение 7 - по прочности режущего инструмента; ограничение 8 - по жесткости режущего инструмента; ограничение 9 - по жесткости заготовки; ограничение 10 - по требуемой шероховатости поверхности.
|
|
|
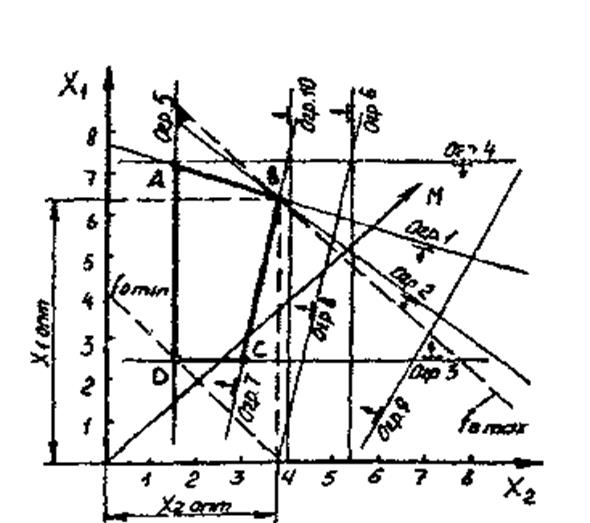
Рис.1 Графическое построение математической модели определения оптимальных режимов
Ограничения 5-10 совместно с рассмотренными выше ограничениями образуют математическую модель процесса резания в аналитическом виде. Кроме технических ограничений, представляемых в виде системы неравенств, в состав модели входит оценочная функция 
.
(14)
Определение оптимальных значений 
и 
может производиться с использованием численных методов линейного программирования с применением ЭВМ. В рассматриваемом примере задача будет решена графическим методом. В этом случае каждое техническое ограничение представляется граничной прямой, которая определяет полуплоскость, где возможно существование решений системы неравенств. Граничные прямые, пересекаясь, образуют многоугольник решений АВСD (рис. 2.1), внутри которого любая точка удовлетворяет всем без исключения неравенствам. Для определения оптимальных значений и под углом 45° к осям 
и 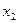строится вектор максимизации М для оценочной функции 
, которая изображается прямой (штриховая линия), перпендикулярной этому вектору. В точке D, где прямая оценочной функции коснется многоугольника решений, функция принимает минимальное значение 
, а в точке В - максимальное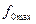 
. Координаты этой точки являются оптимальными значениями и , они определяются графически (рис. 2.1) с учетом принятого масштаба 
и 
.
Численные значения оптимального режима резания вычисляются по следующим зависимостям:
(15)
(16)
Задание
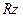Построить математическую модель процесса резания и определить оптимальные режимы резания для точения поверхности заготовки типа вал диаметром 10i мм и длиной = 20i+30 мм, материал – по заданию преподавателя (сталь 45, cт.5, СЧ15, ШЧ15, КЧ35, Сталь 40Х, Сталь 12ХГТ), требуемая шероховатость =40 мкм, глубина резания =0,5+0,1i мм.
Практическая работа №2
|
|
|
