 |
Статическая определимость кинематической цепи
|
|
|
|
СИЛОВОЙ АНАЛИЗ МЕХАНИЗМОВ
Общие сведения и определения. Силы, действующие в механизмах
При проведении силового анализа решаются основные задачи:
1. Определение реакций в кинематических парах механизмов, находящихся под действием заданных внешних сил. Эти реакции затем используются для расчёта звеньев и элементов кинематических пар (например, подшипников) на прочность, жёсткость, долговечность и т.д.
2. Определение уравновешивающей силы 
или уравновешивающего момента 
, приложенных к ведущему звену. Они уравновешивают внешние силы, приложенные к механизму. Эти величины нужны, например, для выбора двигателя, приводящего в движение данный механизм.
Силы, действующие в механизмах
Различают две группы сил.
Движущие силы Рдв или моменты движущих сил Мдв, которые:
– совершают положительную работу;
– направлены в сторону скорости точки приложения силы или под острым углом к ней;
– задаются посредством механической характеристики двигателя.
Силы сопротивления Р С и их моменты М С, которые:
– совершают отрицательную работу;
– направлены противоположно скорости.
В свою очередь силы сопротивления делятся на силы:
– полезного сопротивления Р п.с и моменты М п.с;
– вредного сопротивления: трение в кинематических парах, сопротивление среды, внутреннее сопротивление (например, силы упругости звеньев).
Кроме этого существуют:
– силы веса 
, где r – плотность материала; V – объём звена детали;
– силы инерции 
;
– моменты сил инерции 
, где mu, JS – масса и массовый момент инерции звена;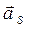 
и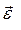 
– линейное и угловое ускорения;
– силы реакций в кинематических парах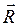 
.
Силы инерции звеньев и моменты сил инерции
|
|
|
Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, могут быть сведены к силе инерции 
, приложенной в центре масс S звена, и паре сил инерции, момент которых обозначим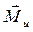 
(рис. 3.1).
– главный вектор сил инерции, или сила инерции; 
– главный момент сил инерции, или момент сил инерции; m – масса звена;
Рис. 3.1. Сила инерции JS – массовый момент инерции относительно
звена и момента центра масс; 
– ускорение центра масс;
сил инерции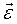 
– угловое ускорение звена.
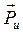и 
направлены в стороны, противоположные ускорениям 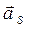и 
.
Для дальнейших расчётов удобно заменить 
и 
одной силой, использовав для этого 3 метода.
Метод замещающих точек подробно представлен в [3. С. 252].
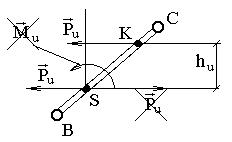Перенос силы 
на плечо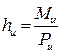 
: момент сил инерции заменяется парой сил 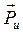с плечом hu (рис. 3.2), причём одна сила приложена к центру масс звена S и направлена противоположно преобразуемой силе , а другая смещена на плечо hu и приложена к точке К – центру качания звена.
Рис. 3.2. Перенос силы на плечо
при замене силы и момента одной силой
Определение центра качания звена через мгновенный центр ускорений (МЦУ).
При этом сила инерции 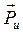переносится параллельно самой себе на расстояние 
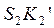(рис. 3.3), вычисленное по формуле
, мм,
где 
– мгновенный центр ускорений звена; 
откладывается в сторону, являющуюся продолжением отрезка 
.
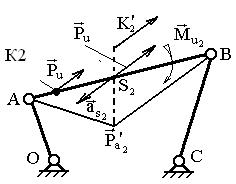
Рис. 3.3. Определение центра качания звена
Статическая определимость кинематической цепи
При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Докажем это положение, проанализировав реакции в кинематических парах (табл.).
| Кинематические пары | Равновесие каждого звена | Известные параметры | Неизвестные параметры |
5-й класс
Вращательная
| 
| Точка приложения | Величина, направление |
Поступательная
| 
| Направление | Величина, точка приложения |
4-й класс
| 
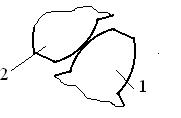
| Точка приложения, направление | Величина |
Примечание. 2, 3, 5 – номера звеньев.
|
|
|
В кинематических парах 5-го класса известно по одному параметру сил реакций, неизвестны два, в кинематических парах 4-го класса известны два параметра, а неизвестен один.
Таким образом, плоская кинематическая цепь, состоящая из кинематических пар 5-го и 4-го классов, имеет 2Р5 + Р4 неизвестных величин сил реакций.
В то же время для одного звена можно составить 3 уравнения статики, а для n звеньев – 3n уравнений статики.
Кинематическая цепь будет статически определима, если число неизвестных величин сил реакций не превышает числа возможных уравнений статики, т.е.
3n = 2P5 + Р4.
Это и есть условие статической определимости кинематической цепи.
Полученное равенство можно записать в виде
3n – 2Р5 – Р4 = 0.
Но запись слева от знака равенства является числом степеней свободы кинематической цепи W, т.е.
W = 3n – 2Р5 – P4 = 0.
Как известно (см. раздел 1 «Структура и классификация механизмов»), таким свойством (W=0) обладают структурные группы, или группы Асура – статически определимые кинематические цепи.
Метод силового анализа, приведенный ниже, называется кинетостатическим, так как для определения сил реакций в кинематических парах, возникающих при движении звеньев, используются уравнения статики.
Порядок (последовательность) силового анализа рычажного механизма:
1. Выделяем из механизма последнюю (крайнюю, наиболее удаленную от ведущего звена) структурную группу и проводим её силовой расчёт, используя уравнения статики.
2. Выделяем из механизма следующую структурную группу и проводим её силовой расчёт.
3. Силовой расчёт заканчиваем силовым расчётом ведущего звена.
Пример
Задан шестизвенный рычажный механизм (рис. 3.4), состоящий из начального механизма (звенья 0 и 1) и структурных групп, образованных звеньями 2 и 3 (двухповодковая структурная группа 2-го класса, 1-го вида) и 4, 5 (структурная группа 2-го класса, 2-го вида).
Рис. 3.4. Шестизвенный рычажный механизм
Решение
1. Проводим силовой расчёт структурной группы 4-5 (определяем неизвестные реакции, если известны внешние силы, действующие на звенья 4 и 5):
|
|
|
2. Проводим силовой расчёт структурной группы 2-3:
3. Проводим силовой расчёт ведущего звена:
|
|
|
