 |
Силовой анализ механизма с учетом сил трения
|
|
|
|
3.5.1. Теоретические основы определения коэффициента трения
Трение в поступательной кинематической паре
При перемещении одного тела (звена механизма) относительно нахо-дящегося с ним в контакте другого тела (звена) в месте их контакта воз-никает сила, сопротивляющаяся перемещению, – сила трения F (рис. 3.16).
Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил 
и 
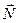равна полной силе реакций в кинематической паре: 
(рис. 3.16).
Рис. 3.16. Схема сил в поступательной кинематической паре
Отношение 
называют коэффициентом трения скольжения в поступательной кинематической паре, а угол 
– углом трения скольжения.
Полная реакция 
отклоняется на угол трения 
в сторону, противоположную скорости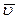 
(см. рис. 3.16).
Величину коэффициента трения скольжения f можно определить экспериментально или по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).
Трение во вращательной кинематической паре
Внешние нагрузки, действующие на вал при его вращении, показаны на схеме рис. 3.17. Здесь 
А – точка приложения нор-мальной реакции 
, причем – равно-действующая всех нор-мальных сил (эпюра этих сил может иметь раз-личный вид), (рис. 3.18); 
– сила трения (равно-действующая всех сил трения, распределенных по поверхности контакта); 
– сила давления цапфы вала
Рис. 3.17. Схема сил во вращательной на опору (корпус подшип-
кинематической паре ника); – сила реакции во
|
|
|
вращательной кинемати-ческой паре, 
; 
; 
– угол трения; r – радиус цапфы (опорной части) вала; 
– радиус круга трения; 
– приведенный коэффициент трения.
Во вращательной кинематической паре (см. рис. 3.15) реакция отстоит от оси вращения на величину радиуса круга трения 
, причем всегда касательна к кругу трения.
Момент трения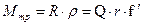 
.
Величину 
можно определить:
– экспериментально (например, используя метод выбега, который описан в «Лабораторном практикуме по теории механизмов и машин») [6];
– по эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис. 3.18): для нового подшипника 
, для изношенного – 
, где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).
Новый подшипник Изношенный подшипник
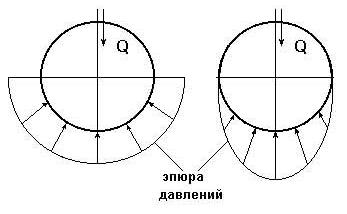
Рис. 3.18. Примерные схемы эпюр давления
в новом и изношенном подшипниках скольжения
Трение качения в высшей кинематической паре
Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах (рис. 3.19). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая сила N совпадает с нормалью. При качении симметрия эпюры нарушается, а сила N смещается в направлении качения на расстояние k.
а б
Рис. 3.19. Примерные схемы сил и эпюр давления
в зоне контакта цилиндра с плоскостью: а – состояние покоя;
б – состояние перекатывания
Здесь – равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения); – нагружающая сила, 
; 
– момент трения качения; 
– плечо силы трения качения или коэффициент трения качения (имеет размерность длины); 
– сила перекатывания.
Условие равновесия перекатывающегося тела в форме моментов можно записать как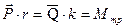 
, откуда 
.
|
|
|
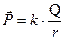3.5.2. Пример учета сил трения при силовом анализе механизма
Пусть задан кривошипно-ползунный механизм с известными внешними силами (рис. 3.20). Необходимо провести силовой анализ механизма, учитывая силы трения в кинематических парах.
|
 |
|
Рис. 3.20. Кинематическая схема кривошипно-ползунного механизма
Сначала проводим силовой анализ механизма без учета сил трения (см. примеры, приведенные выше). При этом определяем силы реакций в кинематических парах. Затем обозначаем силы реакций в кинематических парах, радиусы цапф валов и коэффициенты трения и заносим их в таблицу.
| Кинематические пары Параметры | О | А | Ввр | Впост |
| Силы реакций | R0 | RA | RBвp | RBпост |
| Радиусы цапф | r0 | rA | rB | - |
| Коэффициенты трения | f0 | fA | fBвр | fBпост |
Отразим трение в потерях мгновенных мощностей на трение в кинематических парах: вращательной – N = Мт × ω; поступательной – 
, где Мтр = R×ρ = R×r×f – момент трения во вращательной кинематической паре; 
– сила трения в поступательной кинематической паре.
Применительно к кривошипно-ползунному механизму (см. рис. 3.20) выразим потери мощностей на трение уравнением
N0 + NA + NВвр + NBпост = Мтр × ω1,
где N0, NA, NВвр, NBпост – соответственно потери мощности на трение в кинематических парах О, А, Ввр, Впост; ω1 – угловая скорость кривошипа; Мтр – приведенный к кривошипу момент от всех сил трения в кинематических парах.
Тогда уравнение мощностей запишем в виде
R0 × r0 × f0 × ω1 + RA × rA × fA × (ω1 – ω2) + RBвр × rBвр × fBвр × ω2 +
+RBпост × fBпост × VB = Mтр × ω1.
Из этого уравнения определяем момент трения Мтр на ведущем звене, который затем учитывается при расчете уравновешивающего момента Мур или уравновешивающей силы Рур на ведущем звене механизма.
|
|
|
