 |
А) по формулам Крамера; б) матричным способом; в) методом Гаусса.
|
|
|
|
МАТЕМАТИКА
Контрольная работа
Семестр
Для бакалавриатов направления 19.03.03 «Продукты питания животного происхождения» заочной формы обучения
Бугульма, 2016
Оглавление
Указания по выполнению контрольной работы.. 3
Раздел Линейная алгебра. 4
Раздел Элементы векторного анализа и аналитической геометрии. 16
Раздел Комплексные числа. 32
Приложение 1. 46
Приложение 2. 49
Указания по выполнению контрольной работы
1. Номер варианта контрольной работы выбирается согласно двум последним цифрам зачетной книжки.
Задания выбираются согласно Приложению 1.
3. В заголовке контрольной работы написать:
- фамилию, имя, отчество (полностью);
- курс, № группы;
- № зачетной книжки;
- вариант контрольной работы;
-дата сдачи ее в институт.
3. Работа оформляется в тетради в клетку (оформление решений производить аккуратно, с минимальным количеством исправлений, оставить поля для замечаний).
4. Правила оформления решения задач:
- располагать в порядке номеров, указанных в заданиях, сохраняя их номер
- перед решением каждой задачи выписывать полностью условие
-решение каждой задачи сопровождать объяснением и заканчивать ответом.
Раздел Линейная алгебра
Найти значение матричного многочлена ( 
– единичная матрица):
1. 
2. 
3. 
4. 
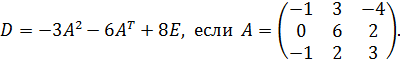
5. 
6. 
7. 
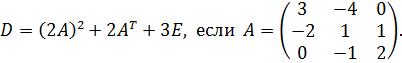
8. 
9. 
10. 
11. 
12. 
13. 
14. 
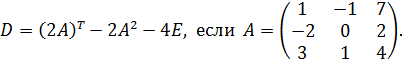
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
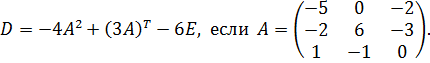
26. 
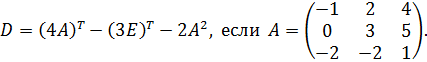
27. 
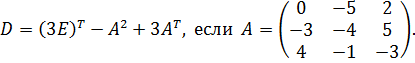
28. 
29. 
30. 
Пример выполнения задания
Найти значение матричного многочлена ( – единичная матрица):
Решение:
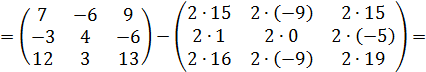
Ответ: 
Вычислить определитель четвертого порядка разложением по элементам ряда:
31. 
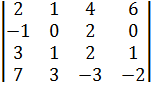
| 32.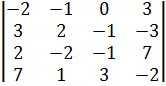 
| 33. 
|
34. 
| 35. 
| 36. 
|
37. 
| 38. 
| 39.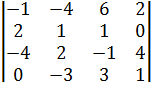 
|
40. 
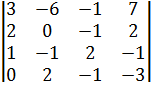
| 41. 
| 42. 
|
43. 
| 44.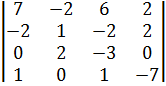 
| 45. 
|
46. 
| 47. 
| 48. 
|
49. 
| 50. 
| 51.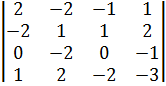 
|
52. 
| 53. 
| 54.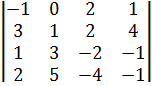 
|
55. 
| 56.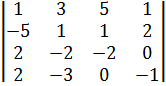 
| 57. 
|
58. 
| 59. 
| 60. 
|
Пример выполнения задания
|
|
|
Вычислить определитель четвертого порядка разложением по элементам ряда: 
Решение:
Разложим определитель согласно следствию теоремы Лапласа: определитель квадратной матрицы равен сумме произведения элементов любой строки (столбца) на их алгебраические дополнения
где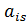 
– элемент определителя, стоящей в 
–ой строке и в столбце 
;
– алгебраическое дополнение элемента .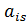
Разложим по первому столбцу:
Ответ: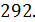 
Решить матричное уравнение
61. 
| 62. 
|
63. 
| 64. 
|
65. 
| 66.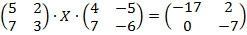 
|
67. 
| 68. 
|
69. 
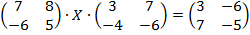
| 70. 
|
71. 
| 72. 
|
73. 
| 74. 
|
75. 
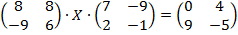
| 76. 
|
77. 
| 78. 
|
79. 
| 80. 
|
81. 
| 82. 
|
83. 
| 84. 
|
85. 
| 86. 
|
87. 
| 88. 
|
89. 
| 90. 
|
Пример выполнения задания
Решить матричное уравнение: 
Решение:
Перепишем данное уравнение в виде: 
где 
Умножим обе части равенства слева на матрицу 
, обратную матрице 
и справа на матрицу 
, обратную матрице 
Ответ: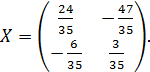 
Исследовать систему на совместимость и решить её:
а) по формулам Крамера; б) матричным способом; в) методом Гаусса.
91. 
| 92.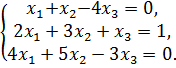 
|
93. 
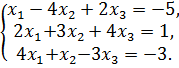
| 94.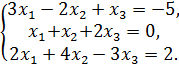 
|
95. 
| 96.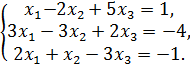 
|
97. 
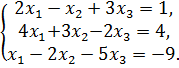
| 98.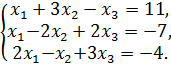 
|
99. 
| 100. 
|
101. 
| 102. 
|
103. 
| 104.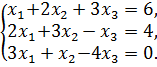 
|
105. 
| 106.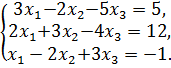 
|
107. 
| 108.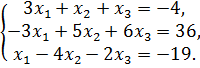 
|
109. 
| 110. 
|
111. 
| 112. 
|
113. 
| 114. 
|
115. 
| 116. 
|
117. 
| 118. 
|
119. 
| 120. 
|
Пример выполнения задания
Исследовать систему 
на совместимость и решить её: а) по формулам Крамера; б) матричным способом; в) методом Гаусса.
Решение:
Исследование системы на совместимость проведем в соответствии с теоремой Кронекера-Капелли: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Найдем ранг расширенной матрицы:
Полученная расширенная матрица имеет ранг равный трем, 
(матрица имеет ступенчатый вид, а количество строк в матрице такого вида определяет ранг).
Проведя аналогичные преобразования над матрицей системы можно также привести ее к ступенчатому виду, и убедиться что ранг матрицы системы также равен трем, 
.
|
|
|
Условие теоремы Кронекера-Капелли выполняется, следовательно, исходная система имеет единственное решение.
а) решим систему по формулам Крамера:
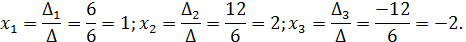
б) решим систему матричным способом.
Перепишем систему в матричном виде:
где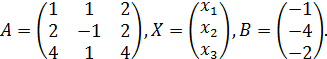 
Полученное матричное уравнение решим, умножив обе части равенства на обратную матрицу с левой стороны:
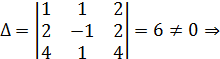существует обратная матрица.
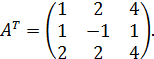
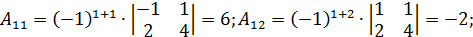
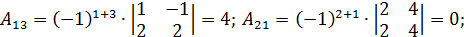
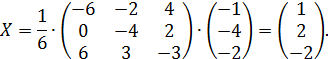
в) решим систему методом Гаусса:
Исходная система примет вид:
Ответ: 
Исследовать на совместимость и решить систему:
121. 
| 122. 
|
123. 
| 124. 
|
125. 
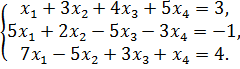
| 126. 
|
127. 
| 128. 
|
129. 
| 130. 
|
131. 
| 132.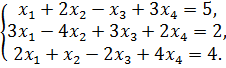 
|
133. 
| 134. 
|
135. 
| 136. 
|
137. 
| 138. 
|
139. 
| 140. 
|
141. 
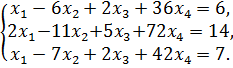
| 142. 
|
143. 
| 144.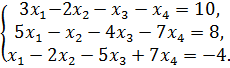 
|
145. 
| 146. 
|
147. 
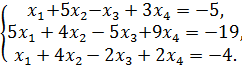
| 148.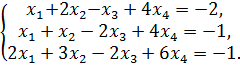 
|
149. 
| 150. 
|
Пример выполнения задания
Исследовать на совместимость и решить систему: 
Решение:
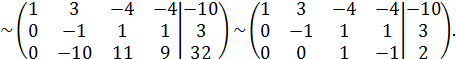
Полученная расширенная матрица имеет ранг равный трем, (матрица имеет ступенчатый вид, а количество строк в матрице такого вида определяет ранг).
Проведя аналогичные преобразования над матрицей системы можно также привести ее к ступенчатому виду, и убедиться что ранг матрицы системы также равен трем, .
Условие теоремы Кронекера-Капелли выполняется, следовательно, исходная система имеет единственное решение – совместная.
Поскольку ранг рассмотренных матриц равен 3, а число неизвестных переменных 4, т.е.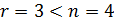 
, то делаем вывод о неопределенности данной системы линейных уравнений.
Так как 
, значит, три неизвестные исходной системы являются основными, и одна – вспомогательная. Выберем основные неизвестные.
Проверим являются ли основными неизвестные 
?
Составим по матрице ступенчатого вида, определитель из коэффициентов при выбранных переменных:
– основные неизвестные, а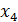 
– вспомогательная переменная.
По матрице ступенчатого вида составим систему уравнений и разрешим ее относительно основных переменных.
Ответ: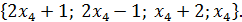 
Решить однородную систему линейных алгебраических уравнений:
151. 
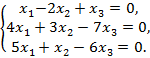
| 152. 
| 153.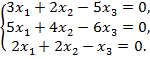 
|
154. 
| 155. 
| 156.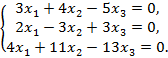 
|
157. 
| 158. 
| 159.
|
160. 
| 161. 
| 162. 
|
163. 
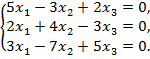
| 164. 
| 165. 
|
166. 
| 167.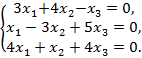 
| 168. 
|
169. 
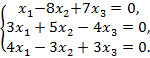
| 170. 
| 171. 
|
172. 
| 173. 
| 174.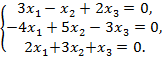 
|
175. 
| 176. 
| 177. 
|
178. 
| 179.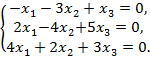 
| 180. 
|
Пример выполнения задания
Решить однородную систему линейных алгебраических уравнений:
|
|
|
Решение:
Вычислим ранг матрицы:
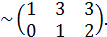
Поскольку ранг рассмотренной матрицы равна 2, а число неизвестных переменных 3, т.е.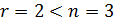 
, то делаем вывод о неопределенности данной системы линейных уравнений.
Проверим являются ли основными неизвестные 
?
Составим по матрице ступенчатого вида, определитель из коэффициентов при выбранных переменных:
– основные неизвестные, а 
– вспомогательная переменная.
По матрице ступенчатого вида составим систему уравнений и разрешим ее относительно основных переменных.
Ответ: 
|
|
|
