 |
б) составить уравнение гиперболы, фокусы и вершины которой находятся соответственно в вершинах и фокусах найденного в п. а) эллипса. Найти её асимптоты, директрисы, эксцентриситет. Сделать чертеж.
|
|
|
|
в) составить уравнение параболы с вершиной в начале координат, симметричной относительно оси  и проходящей через точку
и проходящей через точку  . Найти её фокус, уравнение директрисы. Сделать чертеж.
. Найти её фокус, уравнение директрисы. Сделать чертеж.
Решение:
а) Каноническое уравнение эллипса имеет вид:

Где  и
и  – большая и малая полуоси эллипса.
– большая и малая полуоси эллипса.
По условию, эллипс проходит точки  , значит, их координаты удовлетворяют уравнению эллипса.
, значит, их координаты удовлетворяют уравнению эллипса.
Координаты точки  , удовлетворяют уравнению эллипса, т.е.
, удовлетворяют уравнению эллипса, т.е.



Уравнение эллипса имеет вид:

Фокусы эллипса имеют координаты: 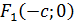 и
и  , где
, где 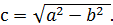
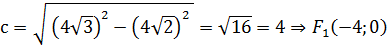 и
и  .
.
Эксцентриситет эллипса равен: 

Уравнения директрис эллипса имеют вид: 
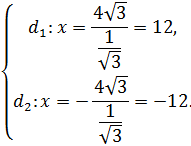
Вершины эллипса имеют координаты: 

б) Вершины гиперболы совпадают с фокусами, найденного в пункте а) эллипса, т.е. точки 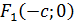 и
и  являются вершинами гиперболы. Значит большая полуось гиперболы равна 4 (
являются вершинами гиперболы. Значит большая полуось гиперболы равна 4 ( ).
).
Фокусы гиперболы совпадают с вершинами эллипса, лежащими на оси  ,т.е. с точками:
,т.е. с точками:  ;
;  .
.
Соответственно координаты фокусов гиперболы будут: 
 ;
;  .
.
Так как  то имеем
то имеем 
Уравнение гиперболы примет вид:

Эксцентриситет гиперболы равен: 

Уравнения директрис эллипса имеют вид: 
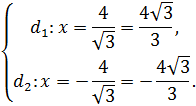
Уравнения асимптот гиперболы имеют вид:



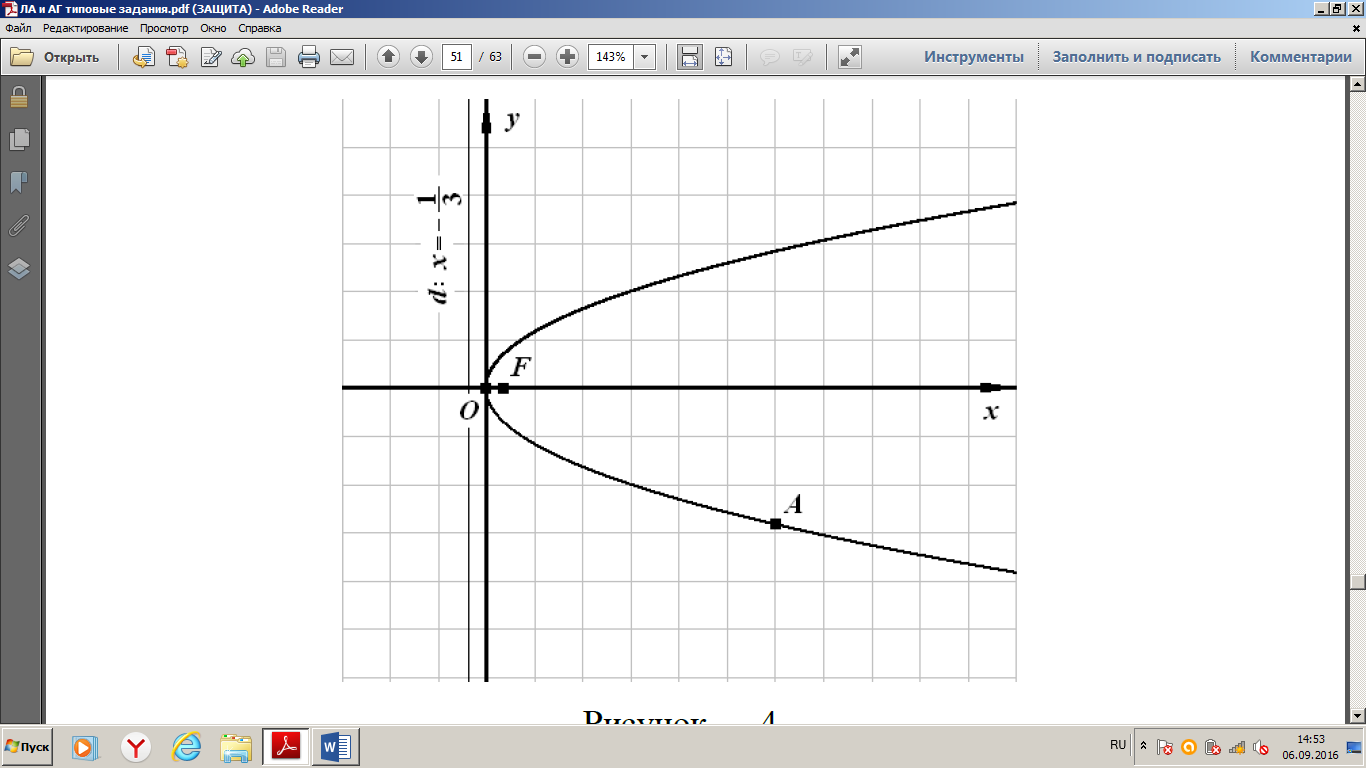
в) Ветви параболы симметричны  оси и она проходит через точку
оси и она проходит через точку  , т.е ветви направлены влево от начала координат, то её уравнение имеет вид:
, т.е ветви направлены влево от начала координат, то её уравнение имеет вид:
 .
.
Парабола проходит через точку  :
:  .
.

Фокус данной параболы имеет координаты: 
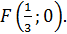
Уравнение директрисы: 

Ответ:
Даны координаты вершин пирамиды  с вершиной в точке
с вершиной в точке  .Найти:
.Найти:
а) площадь грани  ;
;
б) объем пирамиды  ;
;
в) уравнение ребер  и
и  , указав координаты направляющих векторов;
, указав координаты направляющих векторов;
г) уравнения граней  и
и  , указав координаты их нормалей;
, указав координаты их нормалей;
д) длину высоты  ;
;
е) угол между плоскостью основания  и боковым ребром
и боковым ребром  ;
;
|
|
|
ж) угол между плоскостью основания  и боковой гранью
и боковой гранью  ;
;
з) уравнение плоскости, проходящей через вершину  параллельно основанию
параллельно основанию  ;
;
и) уравнение прямой, проходящей через точку  параллельно ребру
параллельно ребру  ;
;
к) уравнение прямой, проходящей через точку  перпендикулярно плоскости основания
перпендикулярно плоскости основания  ;
;
л) угол между боковыми ребрами  и
и  .
.
271. 
|
272. 
|
273. 
|
274. 
|
275. 
|
276. 
|
277. 
|
278. 
|
279. 
|
280. 
|
281. 
|
282. 
|
283. 
|
284. 
|
285. 
|
286. 
|
287. 
|
288. 
|
289. 
|
290. 
|
291. 
|
292. 
|
293. 
|
294. 
|
295. 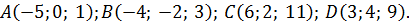
|
296. 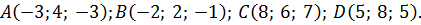
|
297. 
|
298. 
|
299. 
|
300. 
|
Пример выполнения задания
Даны координаты вершин пирамиды:  .Найти:
.Найти:
а) площадь грани  ;
;
б) объем пирамиды  ;
;
в) уравнение ребер  и
и  , указав координаты направляющих векторов;
, указав координаты направляющих векторов;
г) уравнения граней  и
и  , указав координаты их нормалей;
, указав координаты их нормалей;
д) длину высоты  ;
;
е) угол между плоскостью основания  и боковым ребром
и боковым ребром  ;
;
ж) угол между плоскостью основания  и боковой гранью
и боковой гранью  ;
;
з) уравнение плоскости, проходящей через вершину  параллельно основанию
параллельно основанию  ;
;
и) уравнение прямой, проходящей через точку  параллельно ребру
параллельно ребру  ;
;
к) уравнение прямой, проходящей через точку  перпендикулярно плоскости основания
перпендикулярно плоскости основания  ;
;
л) угол между боковыми ребрами  и
и  .
.
Решение:
а) Вычислить площадь грани  .
.
Для вычисления площади грани  , используем формулу определяющую площадь треугольника, построенного на векторах
, используем формулу определяющую площадь треугольника, построенного на векторах  и
и  :
:

где  – векторное произведение векторов
– векторное произведение векторов  и
и  , которое может быть найдено следующим образом:
, которое может быть найдено следующим образом:








б) Вычислить объем пирамиды  .
.
Объем пирамиды, построенной на векторах  можно вычислить по формуле:
можно вычислить по формуле:

Где  – смешанное произведение векторов
– смешанное произведение векторов  ,
,  и
и  , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:
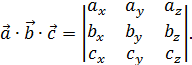


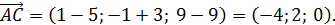


в) Найти уравнение ребер  и
и 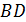 , указав координаты направляющих векторов.
, указав координаты направляющих векторов.
Уравнение ребра можно найти как уравнение прямой, проходящей через заданные точки  и
и  по формуле:
по формуле:

где  – направляющий вектор прямой.
– направляющий вектор прямой.




г) Найти уравнения граней  и
и 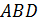 , указав координаты их нормалей.
, указав координаты их нормалей.
|
|
|
Уравнение грани можно определить как уравнение плоскости проходящей через три заданные точки  ,
,  и
и  по следующей формуле:
по следующей формуле:



 – координаты нормали грани
– координаты нормали грани  .
.


 – координаты нормали грани
– координаты нормали грани 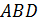 .
.
д) Найти длину высоты 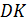 .
.
Длину высоты пирамиды определим из формулы для нахождения объема пирамиды:

Где  – длина высоты, опущенной на основание пирамиды.
– длина высоты, опущенной на основание пирамиды.

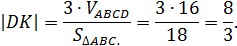
е) Найти угол между плоскостью основания  и боковым ребром
и боковым ребром  .
.
За угол между прямой и плоскостью принимают угол между этой прямой и её проекцией на данную плоскость. Она может быть вычислена по формуле:

Где  – нормальный вектор плоскости,
– нормальный вектор плоскости,  – направляющий вектор прямой.
– направляющий вектор прямой.
Эту формулу можно записать в координатном виде:




ж) Вычислить угол между плоскостью основания  и боковой гранью
и боковой гранью 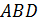 .
.
За угол между двумя плоскостями можно принять угол между их нормальными векторами, который может быть вычислен по формуле:




з) Найти уравнение плоскости, проходящей через вершину  параллельно основанию
параллельно основанию  .
.
Пусть  уравнение искомой плоскости
уравнение искомой плоскости  . По условию плоскость
. По условию плоскость  параллельна плоскости
параллельна плоскости  . Используем условие параллельности плоскостей: две плоскости параллельны, если координаты их нормальных векторов пропорциональны, т.е
. Используем условие параллельности плоскостей: две плоскости параллельны, если координаты их нормальных векторов пропорциональны, т.е

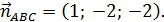 Поскольку искомая плоскость параллельна
Поскольку искомая плоскость параллельна  то
то  .
.
Плоскость  проходит через точку
проходит через точку  , т.е
, т.е
 .
.
Уравнение плоскости  параллельной грани
параллельной грани  , имеет вид:
, имеет вид:
 .
.
и) Найти уравнение прямой, проходящей через точку  параллельно ребру
параллельно ребру  .
.
Используем формулу, определяющую каноническое уравнение прямой в пространстве:

Где  – координаты произвольной точки прямой,
– координаты произвольной точки прямой,  – координаты любого ее направляющего вектора.
– координаты любого ее направляющего вектора.


к) Найти уравнение прямой, проходящей через точку  перпендикулярно плоскости основания
перпендикулярно плоскости основания  .
.
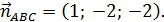

л) Найти угол между боковыми ребрами  и
и 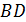 .
.
Угол между двумя прямыми  и
и 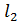 определим как угол между их направляющими векторами
определим как угол между их направляющими векторами  и
и 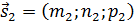 по формуле:
по формуле:
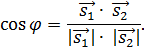



Раздел Комплексные числа
Представьте число в алгебраической форме:
301. 
| 302. 
| 303. 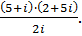
|
304. 
| 305. 
| 306. 
|
307. 
| 308. 
| 309. 
|
310. 
| 311. 
| 312. 
|
313. 
| 314. 
| 315. 
|
316. 
| 317. 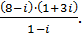
| 318. 
|
319. 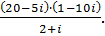
| 320. 
| 321. 
|
322. 
| 323. 
| 324. 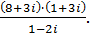
|
325. 
|
Пример выполнения задания
Представьте число в алгебраической форме: 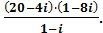
Решение:
Умножим числитель и знаменатель на число, сопряженное знаменателю:
|
|
|


Ответ: 
Найдите на комплексной плоскости множество точек, советующих множеству:
326. 
|
327. 
|
328. 
|
329. 
|
330. 
|
331. 
|
332. 
|
333. 
|
334. 
|
Пример выполнения задания
Найдите на комплексной плоскости множество точек, советующих множеству:  .
.
Решение:
Обозначим через  множество, состоящее из точек плоскости, расположенных между прямыми
множество, состоящее из точек плоскости, расположенных между прямыми  и
и  и содержащих точки самих прямых, через
и содержащих точки самих прямых, через 
множество, состоящее из точек плоскости, расположенных между прямыми
 и
и  и содержащих точки самих прямых. Искомое множество
и содержащих точки самих прямых. Искомое множество  находится как пересечение множеств
находится как пересечение множеств  и
и  . На рис. это все внутренние точки прямоугольника, вершинами которого являются точки
. На рис. это все внутренние точки прямоугольника, вершинами которого являются точки 
 ,
, 
 стороны прямоугольника принадлежат искомому множеству.
стороны прямоугольника принадлежат искомому множеству.
Найдите на комплексной плоскости множество точек, советующих множеству:
335. 
|
336. 
|
337. 
|
338. 
|
339. 
|
340. 
|
341. 
|
342. 
|
Пример выполнения задания
Найдите на комплексной плоскости множество точек, советующих множеству: 
Решение:
Выясним геометрический смысл разности
 Известно, что каждому комплексному числу
Известно, что каждому комплексному числу 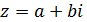 соответствует некоторый радиус-вектор с началом в начале координат и концом в точке с координатами
соответствует некоторый радиус-вектор с началом в начале координат и концом в точке с координатами  Мы имеем два комплексных числа – искомое
Мы имеем два комплексных числа – искомое  , ему соответствует точка с координатами
, ему соответствует точка с координатами  и число
и число  с соответствующей точкой с координатами
с соответствующей точкой с координатами  Тем самым определены два вектора
Тем самым определены два вектора  и
и  .
.
Тогда разности комплексных чисел  будет соответствовать вектор
будет соответствовать вектор 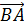 ,
, имеющий начало в точке
 и конец в точке
и конец в точке  . По условию задачи
. По условию задачи  , т.е. длина вектора
, т.е. длина вектора 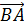 должна быть больше или равна двум и меньше или равна пяти. Если проведем две окружности с центром в точке
должна быть больше или равна двум и меньше или равна пяти. Если проведем две окружности с центром в точке  и радиусами, равными 2 и 5, то точки искомого множества лежат на этих окружностях и между ними, так как расстояние от точки
и радиусами, равными 2 и 5, то точки искомого множества лежат на этих окружностях и между ними, так как расстояние от точки  до этих точек удовлетворяют условию задачи.
до этих точек удовлетворяют условию задачи.
Найдите на комплексной плоскости множество точек, советующих множеству:
343. 
|
344. 
|
345. 
|
346. 
|
347. 
|
348. 
|
349. 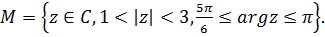
|
350. 
|
Пример выполнения задания
Найдите на комплексной плоскости множество точек, советующих множеству: 
Решение:
Пусть некоторая точка принадлежит  и соответствует комплексному числу
и соответствует комплексному числу  , где
, где  . По условию задачи имеем:
. По условию задачи имеем:  ,
, 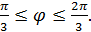 . Так как модуль комплексного числа определяет расстояние соответствующей точки от начала координат, то согласно условию задачи все точки, принадлежащие искомому множеству
. Так как модуль комплексного числа определяет расстояние соответствующей точки от начала координат, то согласно условию задачи все точки, принадлежащие искомому множеству  , находятся от начала координат на расстоянии меньше 5, т.е. все они лежат внутри окружности с центром в начале координат радиусом, равным 5.
, находятся от начала координат на расстоянии меньше 5, т.е. все они лежат внутри окружности с центром в начале координат радиусом, равным 5.
|
|
|
Известно, что аргумент комплексного числа – это угол между положительным направлением оси абсцисс и радиус-вектором из начала координат в точку, соответствующую данному числу. Поэтому точки искомого множества расположены между лучами, выходящими из начала координат и образующими с положительным направлением оси абсцисс углы, равные  и
и 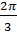 , а также лежащими на этих лучах.
, а также лежащими на этих лучах.
Обозначим через  множество
множество  а через
а через  множество
множество  . Тогда искомое множество
. Тогда искомое множество  и представляет собой часть круга (сектор) с центром в начале координат и радиусом, равным 5, расположенную между лучами, исходящими из начала координат и образующими с положительным направлением оси абсцисс углы
и представляет собой часть круга (сектор) с центром в начале координат и радиусом, равным 5, расположенную между лучами, исходящими из начала координат и образующими с положительным направлением оси абсцисс углы 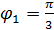 и
и  . Отрезки лучей принадлежат данному множеству, за исключением начала координат, так как для числа
. Отрезки лучей принадлежат данному множеству, за исключением начала координат, так как для числа  аргумента не существует. Дуга окружно
аргумента не существует. Дуга окружно сти также не входит в искомое множество.
Найти значение  и
и  чисел
чисел  , соответствующих точкам, заштрихованной области:
, соответствующих точкам, заштрихованной области:
| 351. | 352. | 353. |
| 354. | 355. | 356. |
| 357. | 358. | 359. |
| 360. |
Пример выполнения задания
Найти значение  и
и  чисел
чисел  , соответствующих точкам, заштрихованной области:
, соответствующих точкам, заштрихованной области:
Решение:
Пусть  – комплексное число, соответствующее одной из точек заштрихованной области
– комплексное число, соответствующее одной из точек заштрихованной области  ,
,  , где
, где  и
и 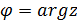 . Из рис. видно, что
. Из рис. видно, что  и
и 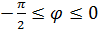 или
или  .
.
Таким образом, множество точек заштрихованной области соответствует множеству комплексных чисел:

или

Найдите значение  и
и 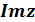 чисел
чисел  , соответствующих точкам заштрихованной области:
, соответствующих точкам заштрихованной области:
| 361. | 362. | 363. |
| 364. | 365. | 366. |
| 367. | 368. | 369. |
| 370. | 371. | 372. |
| 373. | 374. | 375. |
Пример выполнения задания
Найдите значение  и
и 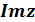 чисел
чисел  , соответствующих точкам заштрихованной области:
, соответствующих точкам заштрихованной области:
Решение:
Обозначим искомое множество через  . Пусть
. Пусть  – произвольная точка заштрихованной фигуры и
– произвольная точка заштрихованной фигуры и  – ее декартовы координаты.
– ее декартовы координаты.
Легко заметить, что  и
и  . Точке
. Точке  соответствует комплексное число
соответствует комплексное число  .
.
Таким образом, множество  состоит из комплексных чисел
состоит из комплексных чисел  , для которых
, для которых 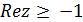 ,
,  , т.е.
, т.е.  .
.
Найдите значения действительных  и
и  :
:
376. 
|
377. 
|
378. 
|
379. 
|
380. 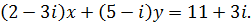
|
381. 
|
382. 
|
383. 
|
384. 
|
385. 
|
386. 
|
387. 
|
388. 
|
389. 
|
390. 
|
391. 
|
392. 
|
393. 
|
394. 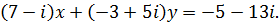
|
395. 
|
396. 
|
397. 
|
398. 
|
399. 
|
400. 
|
Пример выполнения задания
Найдите значения действительных  и
и  из уравнения
из уравнения

Решение:
В правой части уравнения стоит комплексное число, записанное в алгебраической форме. Преобразуем левую часть уравнения так, чтобы получить алгебраическую форму комплексного числа. Получаем:
|
|
|

На основании условия равенства комплексных чисел в алгебраической форме находим, что искомые числа  и
и  являются решением системы линейных уравнений:
являются решением системы линейных уравнений:

Ответ: 
Решите систему уравнений:
401. 
| |
402. 
| |
403. 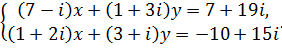
| |
404. 
| |
405. 
| |
406. 
| |
407. 
| |
| 408. | |
|
|
|


