 |
Раздел Элементы векторного анализа и аналитической геометрии
|
|
|
|
Даны координаты точек  ,
,  и
и  в системе
в системе  . Найти:
. Найти:
а) координаты векторов  их разложение по ортам
их разложение по ортам  и их модули;
и их модули;
б) угол между векторами  ;
;
в) направляющие косинусы векторов  ;
;
г) проекцию вектора  на вектор
на вектор 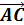 .
.
181. 
| 182. 
|
183. 
| 184. 
|
185. 
| 186. 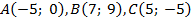
|
187. 
| 188. 
|
189. 
| 190. 
|
191. 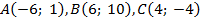
| 192. 
|
193. 
| 194. 
|
195. 
| 196. 
|
197. 
| 198. 
|
199. 
| 200. 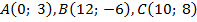
|
201. 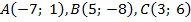
| 202. 
|
203. 
| 204. 
|
205. 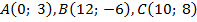
| 206. 
|
207. 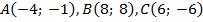
| 208. 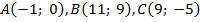
|
209. 
| 210. 
|
Пример выполнения задания
Даны координаты точек  ,
,  и
и  в системе
в системе  . Найти:
. Найти:
а) координаты векторов  их разложение по ортам
их разложение по ортам  и их модули;
и их модули;
б) угол между векторами  ;
;
в) направляющие косинусы векторов  ;
;
г) проекцию вектора  на вектор
на вектор 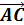 .
.
Решение:
а) Найти координаты векторов  их разложение по ортам
их разложение по ортам 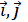 и их модули.
и их модули.
Произвольный вектор 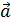 в прямоугольной системе координат
в прямоугольной системе координат  , может быть представлен в виде:
, может быть представлен в виде:

Данное представление вектора  называется его разложением по ортам координатных осей
называется его разложением по ортам координатных осей 
Если вектор задан начальной  и конечной точкой
и конечной точкой 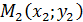 , то данное разложение может быть представлено в виде:
, то данное разложение может быть представлено в виде:



Модуль вектора  определяется по формуле:
определяется по формуле:
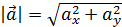 , где вектор
, где вектор  задается координатами
задается координатами  .
.


б) Найти угол между векторами 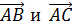 .
.
Воспользуемся формулой

где  – скалярное произведение векторов, которое вычисляется по формуле:
– скалярное произведение векторов, которое вычисляется по формуле:
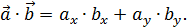


в) Найти направляющие косинусы векторов 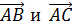 .
.
Направление произвольного вектора 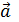 определяется углами
определяется углами 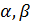 образованными им с координатными осями. Косинусы этих углов называются направляющими косинусами и определяются по формулам:
образованными им с координатными осями. Косинусы этих углов называются направляющими косинусами и определяются по формулам:



г) Найти проекцию вектора  на вектор
на вектор  .
.
Воспользуемся формулой
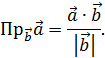

Даны координаты вершин треугольника  . Найти:
. Найти:
а) длины сторон треугольника;
б) уравнения сторон треугольника, указать их угловые коэффициенты и координаты направляющих и нормальных векторов соответственно;
|
|
|
в) угол  треугольника
треугольника  ;
;
г) уравнение высоты  и ее длину;
и ее длину;
д) уравнение медианы  ;
;
е) уравнение прямой, проходящей через точку  , параллельно стороне
, параллельно стороне  ;
;
ж) координаты точки  , расположенной симметрично точке относительно высоты
, расположенной симметрично точке относительно высоты  ;
;
З) сделать чертеж.
211. 
| 212. 
|
213. 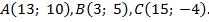
| 214. 
|
215. 
| 216. 
|
217. 
| 218. 
|
219. 
| 220. 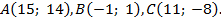
|
221. 
| 222. 
|
223. 
| 224. 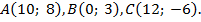
|
225. 
| 226. 
|
227. 
| 228. 
|
229. 
| 230. 
|
231. 
| 232. 
|
233. 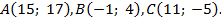
| 234. 
|
235. 
| 236. 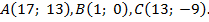
|
237. 
| 238. 
|
239. 
| 240. 
|
Пример выполнения задания
Даны координаты вершин треугольника  . Найти:
. Найти:
а) длины сторон треугольника;
б) уравнения сторон треугольника, указать их угловые коэффициенты и координаты направляющих и нормальных векторов соответственно;
в) угол  треугольника
треугольника  ;
;
г) уравнение высоты  и ее длину;
и ее длину;
д) уравнение медианы  ;
;
е) уравнение прямой, проходящей через точку  , параллельно стороне
, параллельно стороне  ;
;
ж) координаты точки  , расположенной симметрично точке
, расположенной симметрично точке  относительно высоты
относительно высоты  ;
;
З) сделать чертеж.
Решение:
а) Найти длины сторон треугольника  .
.
Расстояние  между точками
между точками  и
и 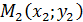 определяется формулой:
определяется формулой:

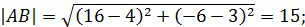


б) Найти уравнения сторон треугольника, указать их угловые коэффициенты и координаты направляющих и нормальных векторов соответственно.
Уравнение прямой проходящей через точки  и
и 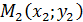 определяется формулой:
определяется формулой:

Если прямая задана своим общим уравнением  , то нормальный
, то нормальный  и направляющий
и направляющий  вектора этой прямой имеют следующие координаты:
вектора этой прямой имеют следующие координаты:
 и
и 

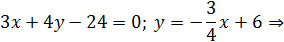
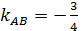 – угловой коэффициент прямой
– угловой коэффициент прямой  ,
, 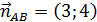 и
и 

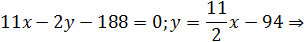
 – угловой коэффициент прямой
– угловой коэффициент прямой 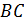 ,
,  и
и 


 – угловой коэффициент прямой
– угловой коэффициент прямой  ,
,  и
и 
в) Найти угол 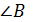 треугольника
треугольника  .
.
Если две прямые  и
и 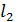 заданы уравнениями с угловым коэффициентами:
заданы уравнениями с угловым коэффициентами:  и
и  , то угол между ними можно найти по формуле:
, то угол между ними можно найти по формуле:




г) Найти уравнение высоты  и ее длину.
и ее длину.
 является высотой треугольника
является высотой треугольника  , значит
, значит 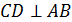 . Используем условие перпендикулярности двух прямых:
. Используем условие перпендикулярности двух прямых:
прямые перпендикулярны, если их угловые коэффициенты обратно пропорциональны и взяты с противоположными знаками, т.е.
|
|
|
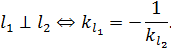
В нашем случае: 
Используем уравнение, проходящие через данную точку 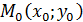 в заданном направлении (оно определяется угловым коэффициентом):
в заданном направлении (оно определяется угловым коэффициентом):


Найдем координаты точки 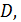 как точку пересечения прямых
как точку пересечения прямых  и
и  :
:


д) Найти уравнение медианы  .
.
Так как  является медианой, то точка
является медианой, то точка  середина отрезка
середина отрезка  . Определим координаты середины отрезка
. Определим координаты середины отрезка  по формуле:
по формуле:


е) Найти уравнение прямой, проходящей через точку  , параллельно стороне
, параллельно стороне  .
.
Пусть искомая прямая 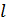 . Тогда, по условию она параллельна прямой
. Тогда, по условию она параллельна прямой  . Используем условие параллельности двух прямых:
. Используем условие параллельности двух прямых:
две прямые параллельны, если они имею равные угловые коэффициенты, т.е.
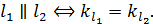

Прямая 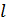 проходит через точку
проходит через точку 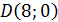 :
:

ж) Найти координаты точки  , расположенной симметрично точке
, расположенной симметрично точке  относительно высоты
относительно высоты  .
.
По условию, точка  симметрична точке
симметрична точке  , относительно высоты
, относительно высоты  , значит, точка
, значит, точка  лежит на прямой
лежит на прямой  и длины отрезков
и длины отрезков  и
и  равны между собой. То есть, точка
равны между собой. То есть, точка 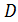 является серединой отрезка
является серединой отрезка  :
:


з) Сделать чертеж.
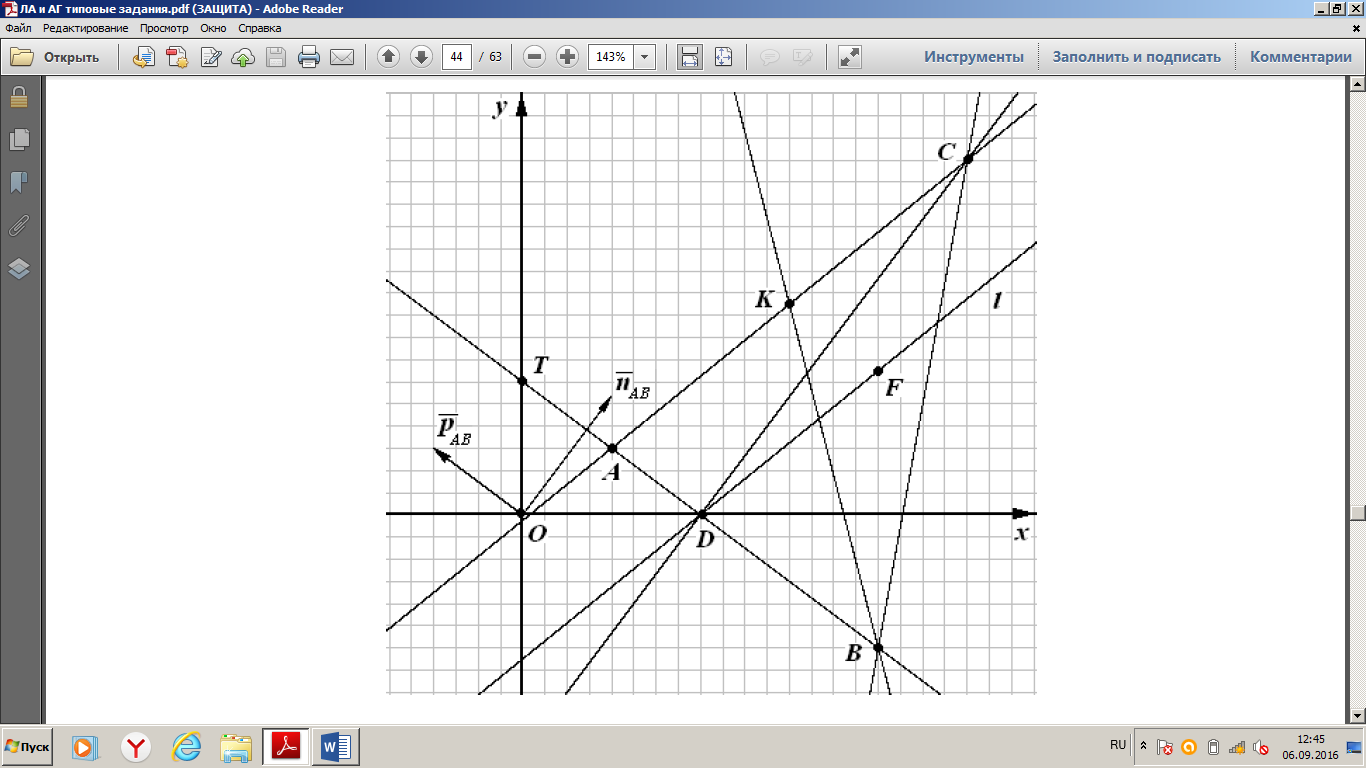
Даны точки 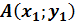 и
и  . Требуется:
. Требуется:
а) составить каноническое уравнение эллипса, проходящего через точки  , наити его полуоси, фокусы, эксцентриситет, уравнение директрис. Сделать чертеж.
, наити его полуоси, фокусы, эксцентриситет, уравнение директрис. Сделать чертеж.
|
|
|


