 |
Метод парных сравнений (МПС).
|
|
|
|
Кафедра гуманитарных и естественных наук
Клюжев Н.А.
Методические указания и контрольные задания
По теме
«ПРИНЯТИЕ РЕШЕНИЙ НА ОСНОВЕ ВЕКТОРНОГО КРИТЕРИЯ:
МЕТОД АНАЛИТИЧЕСКИХ ИЕРАРХИЙ (МАИ)»
Для всех специальностей дневного и заочного отделений
по дисциплинам:
«Системный анализ», «Методы и модели в экономике»
Псков, 2010 г.
Оглавление
| Введение………………………………………………………………… | ||
| 1. | Метод парных сравнений (МПС)…………………………………… | |
| 2. | Процесс анализа иерархий…………………………………………… | |
| 3. | Примеры применения методики……………………………………. | |
| 4. | Задания для выполнения контрольной работы |
Принятие решений на основе векторного критерия:
Метод аналитических иерархий (МАИ)
Введение
Одним из перспективных методов принятия оптимальных решений на многокритериальной основе является достаточно широко известный специалистам процесс аналитической иерархии, разработанный американским ученым Т.Саати. В отечественной литературе этот метод известен как метод аналитических иерархий (МАИ). В основе этого метода лежит метод парных сравнений (МПС), позволяющий «аккумулировать» знания экспертов, накопленный ими в определенной предметной области, в рамках которой моделируется процедура принятия оптимальных решений на основе совокупности, например, частных критериев, т.е. на основе векторного критерия.
Эти знания формализуются согласно процедуре МПС в модель в виде квадратной числовой матрицы суждений (МС) относительной «важности» пары частных критериев для достижения определенной цели  . При парном сравнении частных критериев по цели
. При парном сравнении частных критериев по цели  результат сравнения представляется числом с использованием выбранной шкалы целых положительных чисел.
результат сравнения представляется числом с использованием выбранной шкалы целых положительных чисел.
|
|
|
Особенность матрицы МС в том, что она является обратносимметрической матрицей положительных чисел. Для такой матрицы собственный вектора, соответствующий её наибольшему и положительному собственному значению, после его нормализации даёт в результате вектор приоритетов сравниваемых критериев. Компоненты вектора приоритетов (рангов) критериев интерпретируются как неотрицательные весовые коэффициенты относительного вклада каждого критерия в достижение цели С. Существование и единственность этого собственного значения следует из теоремы Перрона для квадратных матриц, все элементы которых строго положительны. Его значение, близкое размеру матрицы, оценивает степень согласованности парных суждений.
Цель  составляет первый уровень (фокус) иерархической структуры. Второй уровень составляют частные критерии, а третий уровень составляют альтернативы (проекты, сценарии и т.п.), отдельные стороны которых оценивают эти частные критерии.
составляет первый уровень (фокус) иерархической структуры. Второй уровень составляют частные критерии, а третий уровень составляют альтернативы (проекты, сценарии и т.п.), отдельные стороны которых оценивают эти частные критерии.
Далее процесс построение матриц суждений повторяется применительно к множеству альтернатив, сравниваемых теперь по каждому частному критерию, играющему для альтернатив роль цели  . Повторяя эти шаги столько раз, сколько частных критериев входят в векторный критерий, получаем для каждой альтернативы вектор её приоритетов по каждому частному критерию.
. Повторяя эти шаги столько раз, сколько частных критериев входят в векторный критерий, получаем для каждой альтернативы вектор её приоритетов по каждому частному критерию.
Оптимальная альтернатива определяется как альтернатива, для которой скалярное произведение её вектора приоритетов с вектором приоритетов критериев имеет наибольшее значение.
Метод парных сравнений (МПС).
Пусть сформулирована некоторая цель  , на достижение которой оказывают влияние элементы некоторого множества, которые назовём факторами и будем обозначать как
, на достижение которой оказывают влияние элементы некоторого множества, которые назовём факторами и будем обозначать как  . Само множество факторов обозначим как
. Само множество факторов обозначим как  .
.
|
|
|
Как оценить вклад каждого из факторов в достижение цели  ? Для ответа на этот вопрос можно задать на множестве
? Для ответа на этот вопрос можно задать на множестве  отношение по-парного сравнения факторов, а результат сравнения представить положительным числом в соответствии с некоторой числовой шкалой.
отношение по-парного сравнения факторов, а результат сравнения представить положительным числом в соответствии с некоторой числовой шкалой.
Пусть в паре 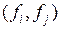 первый элемент-фактор
первый элемент-фактор  сравнивается со вторым элементом-фактором
сравнивается со вторым элементом-фактором 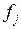 по степени достижения цели
по степени достижения цели  , а результат сравнения оценивается положительным числом
, а результат сравнения оценивается положительным числом  . Если положим, что факторы в паре
. Если положим, что факторы в паре 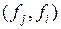 сравниваются по той же цели
сравниваются по той же цели  , то результат сравнения оценивается числом
, то результат сравнения оценивается числом 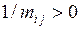 . Предложим следующую шкалу для выбора чисел
. Предложим следующую шкалу для выбора чисел  :
:
ШКАЛА
| Определение отношения | 
|
 равнозначен равнозначен 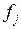
| |
 если нужен компромисс если нужен компромисс 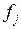
| |
 чуть важнее чуть важнее 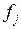
| |
 если нужен компромисс если нужен компромисс 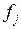
| |
 заметно важнее заметно важнее 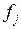
| |
 если нужен компромисс если нужен компромисс 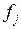
| |
 существенно важнее существенно важнее 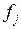
| |
 если нужен компромисс если нужен компромисс 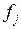
| |
 намного важнее намного важнее 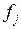
|
Для каждой пары факторов лицо, принимающее решение (ЛПР), исходя из своего понимания соответствия факторов цели  , выбирает значение
, выбирает значение  . Полный набор таких значений образует матрицу суждений эксперта
. Полный набор таких значений образует матрицу суждений эксперта  . Это квадратная матрица размером
. Это квадратная матрица размером 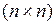 . С учетом правила построения элементов матрицы
. С учетом правила построения элементов матрицы  она будет иметь
она будет иметь  независимых элементов:
независимых элементов:
 ;
; 
 .
.
Поскольку оценки  носят субъективный характер и даже могут быть в конфликте друг с другом (в смысле не выполнения условия транзитивности в суждениях при принятом отношении парного сравнения по цели
носят субъективный характер и даже могут быть в конфликте друг с другом (в смысле не выполнения условия транзитивности в суждениях при принятом отношении парного сравнения по цели  ), а также в силу «грубости» принятой шкалы может иметь место несогласованность суждений. Меру такой несогласованности в матрице
), а также в силу «грубости» принятой шкалы может иметь место несогласованность суждений. Меру такой несогласованности в матрице  можно определить значением модуля разности:
можно определить значением модуля разности:
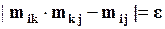 .
.
В случае идеального согласования суждений эта мера равна 0 для всех пар факторов. Например, в случае двух факторов матрица суждений имеет вид:
М =  ,
,
|
|
|


