 |
1) Декодування згортальних кодів. Алгоритм Вітербі.
|
|
|
|
1) Декодування згортальних кодів. Алгоритм Вітербі.
Для декодування згортальних кодів найбільше широко застосовується алгоритм декодування Вітербі (алгоритм максимальної правдоподібності).
Алгоритм декодування Вітербі є повним алгоритмом декодування згортальних кодів, у зв'язку з чим імовірність відмовлення від декодування дорівнює нулеві. Однак при фіксованому коді імовірність помилки декодування буде більше, ніж у неповного декодера. Цей алгоритм практично може бути використаний для двійкових кодів з малою довжиною кодового обмеження — у даний час межею є довжини кодового обмеження 
від 7 до 10. Нижче описується процедура, що являє собою процес декодування по мінімуму відстані від шляху, що генерує кодер.
3. 1. Декодування в умовах відсутності помилок у каналі.
Алгоритм Вітербі має ряд переваг перед іншими, у зв'язку з чим його широко використовують для декодування коротких згортальних кодів. Розглянемо особливості алгоритму на прикладі декодування коду, породжуваного кодером рис. 2, б, зі швидкістю 
. З дискретного двійкового каналу у виді послідовності кадрів 
кодових символів 
(тут 
номер кадру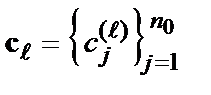 
( 
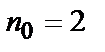) і номер кроку декодування) на вхід декодера надходять кодові посилки – 00. 00. 11. 01. 10. 01. 11. 00. 00. 11. 10. 00. 01. 01. 11. 00. Функціонування декодера (як і кодера) описується процесом «розвитку» решітчастої діаграми, що ілюструється на рис. 9. Тут кружками показані стани кодера (декодера), усередині яких поміщені значення так званих метрик станів 
, ліворуч приведені слова-стани кодера 
( 
), у дужках поруч – інформаційні символи (значення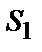 
), що відповідають вихідний (декодованої) послідовності, а під колонками станів зазначені кроки декодування.
|
|
|
«Розвиток» діаграми для кодерів зі швидкістю завжди відбувається за 3 кроки. У початковий момент часу ( крок 0 ) декодер знаходиться в стані « 00 » і вихідна метрика станів – 
.
З рисунка видно, що з кожного стану декодера до кожного нового стану веде дві гілки (див. також діаграму станів рис. 3). У процесі «розвитку» решітчастої діаграми до нового стану вибирається тільки одна гілка.
Номер кроку: 0 1 2 3
Рис. 9. Процес «розвитку» решітчастій діаграми при декодуванні
|
і 
власне на лініях, що зображує гілки) ведуть відповідно до станів « 00 » і « 10 ». Для кожної з цих гілок необхідно обчислити так називану метрику гілки 
(на рисунку позначається кодом над гілкою). Метрика гілки дорівнює відстані Хемминга між кадром символів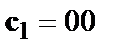 
на вході декодера (на рисунку позначені жирним шрифтом у верхній частині діаграми) і набором символів 
, що відповідають даній гілці на решітчастій діаграмі (рис. 9), тобто числу розрядів, значеннями яких вони відрізняються –
, 
.
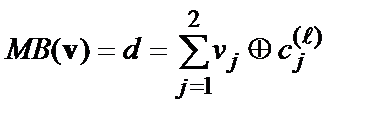Так, наприклад, при 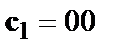для гілки, що веде в стан « 00 », метрика дорівнює 
, а для гілки, що веде в стан « 10 », – 
.
На кожнім 
-м кроці декодування відповідно до алгоритму Вітербі в кожнім із станів решітчастої діаграми виробляються однотипні операції:
1) відшукання метрик 
вхідних шляхів додаванням метрик 
попередніх станів з метриками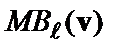 
відповідних гілок;
2) порівняння метрик вхідних шляхів і вибір шляхів з найменшими метриками, величини яких використовують як метрики станів 
поточного кроку декодування;
3) визначення декодованого на даному 
-м кроці символу (у даному випадку дв. розряд) по стану кодера з мінімальною метрикою 
– 
.
У такий спосіб у загальному виді алгоритм Вітербі декодування згортальних кодів на довільному -му кроці описується наступними співвідношеннями:
|
|
|
, 
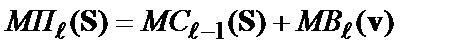; (3*а)
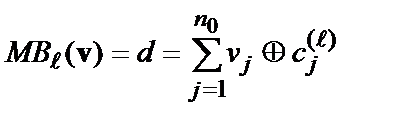; (3*б)
по 
, 
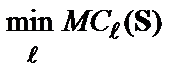. (3*в)
Розглянемо більш докладно зміст декількох перших кроків алгоритму Вітербі декодування приведеної вище тестової кодової послідовності.
Для перших двох кроків (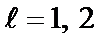 
) роботи алгоритму характерним є те, що на наступні стани замість пари гілок «спирається» тільки по одній гілці. У цих умовах метрика стану 
визначається як сума метрик вхідної гілки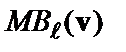 
і попереднього стану 
.
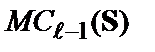Для 1-го кроку декодування метрики станів рівні:
;
.
Далі вибирається шлях до стану з мінімальною метрикою, у даному випадку – до стану 
, і отже декодований інформаційний розряд дорівнює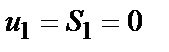 
.
На 2-м кроці декодування з урахуванням значення чергового кадру кодових символів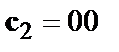 
обчислюються метрики гілок (їх уже 4) і метрики станів по співвідношенням
;
;
;
.
Як і на попередньому кроці мінімальна метрика в стану 
, а значить черговий відновлений інформаційний розряд дорівнює 
.
Зауваження. Уже на цьому кроці може скластися враження, що немає необхідності розраховувати метрики всіх можливих станів і досить обмежитися обчисленням метрик двох станів, у які ведуть шляхи зі стану з мінімальною метрикою, отриманої на попередньому кроці (у даному випадку в 1-м). Однак такий підхід виявляється можливим тільки в припущенні постійної відсутності помилок на приймаючій стороні, що в умовах наявності в каналі шумів і завад по суті є подією неможливим.
Наявність помилок породжує процес «розмноження шляхів, що вижили» і поява хоча б ще одного шляху, що «вижив», приводить до необхідності обліку метрик усіх станів, що буде показано нижче при розгляді роботи декодера Вітербі при перекручуванні в каналі кодової послідовності. Тому починаючи з 2-го кроку в алгоритмі декодування здійснюється розрахунок метрик усіх можливих станів.
Далі алгоритм складається в періодичному повторенні основного кроку, відмінною рисою якого є наявність двох шляхів до кожного наступного стану.
Роблячи попарне порівняння метрик шляхів, що входять у кожен стан, вибирають меншу метрику і неї вважають метрикою даного стану для наступного кроку декодування. Шлях, що входить у даний стан з меншою метрикою, вважають « вижившими » (на діаграмі рис. 9 шляхи, що «вижили», показані жирними лініями). Тонкою лінією показані шляхи, що відкидаються при попарному порівнянні. У результаті порівняння вибирають меншу метрику і неї вважають метрикою даного стану для наступного кроку декодування.
|
|
|
На 3-м (і кожнім наступному 
) кроці реалізуються співвідношення (на кроці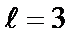 
кадр кодових символів дорівнює 
)
;
;
;
.
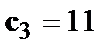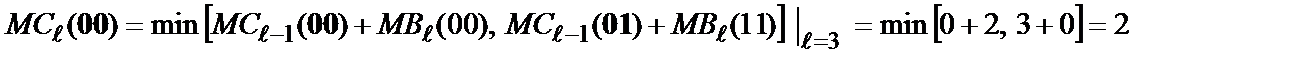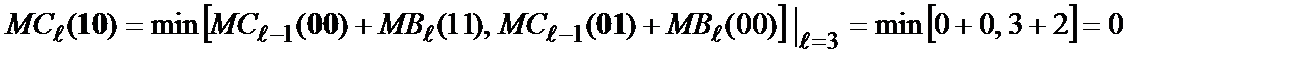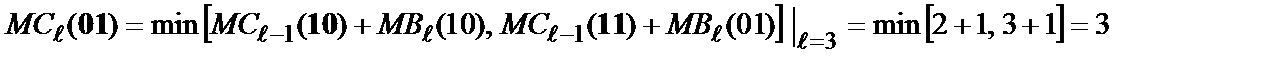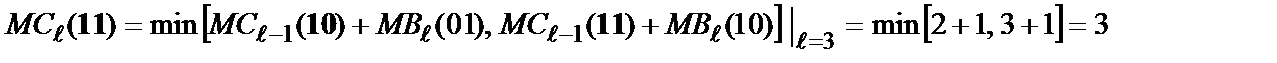На даному кроці мінімальна метрика в стану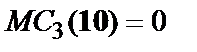 
, а значить черговий відновлений інформаційний розряд дорівнює 
.
Далі алгоритм Вітербі повторює виконання основного кроку по співвідношеннях (3*).
Процес побудови решітчастої діаграми рис. 4 для декодування послідовності виду 00. 00. 11. 01. 10. 01. 11. 00. 00. 11. 10. 00. 01. 01. 11. 00 показаний на рис. 10.
Якщо метрики порівнюваних шляхів однакові, то вибір одного з двох шляхів роблять довільним образом. На кожнім кроці алгоритму при відсутності помилок у каналі в результаті порівняння половина можливих шляхів відкидається і надалі не використовується. Інша половина утворить продовження шляхів для наступного кроку декодування.
У такий спосіб декодер простежує по кодовій решітці шлях, що має мінімальну відстань від шляху, що генерує кодер. Недвійкові коди декодировать декодером Вітербі трудніше, і це можливо лише при дуже малих довжинах кодового обмеження.
|
|
|
