 |
1) Способы описания линейных блоковых кодов.
|
|
|
|
1) Способы описания линейных блоковых кодов.
Существует несколько способов описания линейных блоковых кодов, основными из которых являются матричный и полиномиальный.
Пусть задан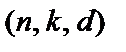 
линейный блоковый код и следовательно существует множество из 
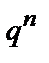канальных кодов 
( 
) и его подмножество из 
кодовых слов, порождаемое информационными словами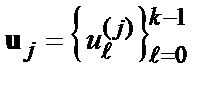 
( 
).
А. Матричный способ описания линейных блоковых кодов
Матричный способ описания линейных блоковых кодов особенно удобен для описания систематических кодов, в которых положение информационных и проверочных разрядов в слове четко определено.
Для кодирования информационного слова 
используют соотношение
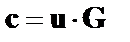. (2)
Задаваемое этим равенством соответствие определяет кодер и зависит от выбора базисных векторов в качестве строк (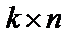 
)-мерной порождающей матрицы 
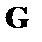. Для систематического кода порождающая матрица – блочная, и может быть представлена следующим образом –
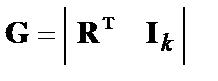а) или 
, б) (3)
где 
– ( 
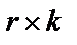)-мерная матрица, задающая способ формирования 
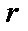проверочных разрядов из имеющихся 
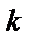информационных (здесь и далее символ «т» обозначает транспонирование);
– ( 
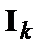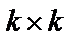)-мерная единичная матрица.
Вариант а) и б) отличаются расположением в кодовом слове информационных и проверочных разрядов. Так при использовании матрицы 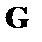(3а) проверочные разряды располагаются в младших разрядах кодового слова (именно этот вариант матрицы 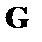будет использоваться для описания процесса кодирования в дальнейшем).
Пример 3.
Рассмотрим порождающую матрицу 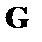вида (3а) простейшего двоичного кода с проверкой на четность (код положительного паритета) для 
и 
( 
)
|
|
|
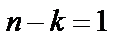, где 
.
Пусть 
. Тогда кодовое слово равно
,
в котором младший разряд является проверочным (битом четности или паритета).
Таким образом, матрица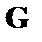 
является компактным описанием линейного блокового кода и формально может быть использована для «порождения» как систематических (вида (3) ), так и несистематических (способ представления будет рассмотрен ниже) блоковых линейных помехоустойчивых кодов.
Пусть задана ( 
)-мерная матрица 
, ортогональная порождающей матрице 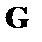, для которой справедливы равенства
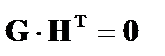а) или 
, (4)
где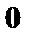 
– ( 
)-мерная нулевая матрица.
Очевидно, что любое «порожденное» матрицей 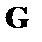кодовое слово ортогонально каждой строке матрицы и следовательно справедливо равенство
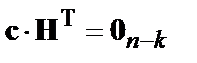, (5)
где 
– ( 
)-мерный нулевой вектор-строка.
Матрица , обладающая свойствами (4), называется проверочной матрицей и также используется для описания линейных блоковых кодов. Соответствующая порождающей линейный код матрице 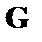вида (3) проверочная матрица имеет вид
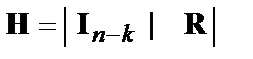а) или 
. б) (6)
Для случая примера 3 проверочная матрица (6а) равна
.
Пример 4.
Сформировать порождающую матрицу 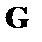вида (3а) для систематического циклического (7, 4, 3)-кода, порождаемого многочленом 
.
Проверочная матрица вида (6а) для циклического (7, 4, 3)-кода Хэмминга строится из элементов расширенного поля Галуа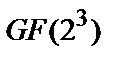 
по модулю , а именно
или (после представления степени примитивного элемента соответствующим полиномом) в виде
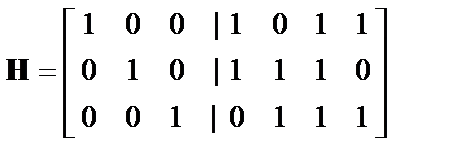. (6в)
Отсюда порождающая матрица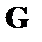 
(3а) имеет вид
.
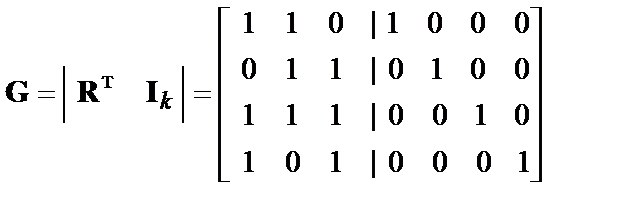Равенство (5) может быть использовано на этапе декодирования принимаемых кодовых последовательностей для обнаружения возможных ошибок в канале, а в ряде случаев и для их исправления.
|
|
|
Пусть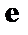 
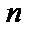-мерный вектор-строка ошибок в канале и принятая кодовая последовательность 
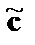определяется по соотношению
.
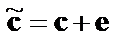Тогда ( )-мерный вектор-строка 
, часто называемый синдромом, равен
. (7)
Очевидно, что если вектор 
, то и вектор синдрома (7) нулевой. Равенство вектора синдрома нулю свидетельствует либо об отсутствии ошибок в канале, либо о возникновении большего числа ошибок, чем может обнаружить код. В противном случае вектор 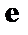содержит нули в «безошибочных» разрядах и значения 
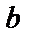из алфавита кода мощности 
в «ошибочных» разрядах ( 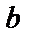– величина «рассогласования» переданного и принятого кода, для двоичного кода 
).
Проиллюстрируем возможность обнаружения и исправления однократной ошибки в канале на примере.
|
|
|
