 |
Пример 5. Б. Полиномиальный способ описания линейных блоковых кодов. Примечание.. Далее эмулируем ошибку в канале
|
|
|
|
Пример 5.
Передать в канал информационное слово 
, используя систематический код, рассмотренный в примере 4. Оценить вектор синдрома 
при ошибке в канале, заданной вектором ошибок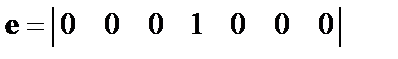 
(ошибка в разряде 
).
По соотношению (2) формируем кодовое слово
.
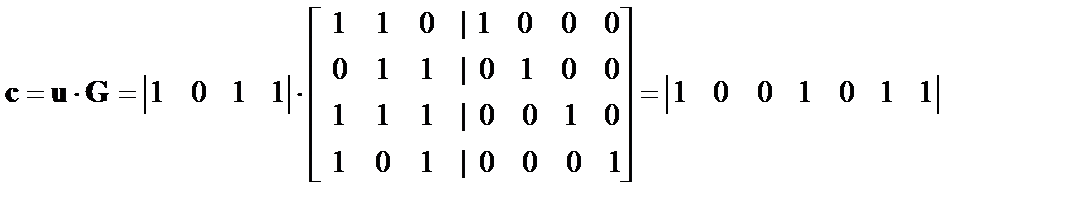Далее эмулируем ошибку в канале
.
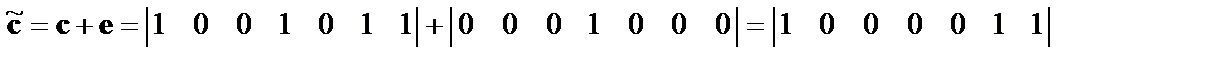По соотношению (7) находим вектор синдрома 
.
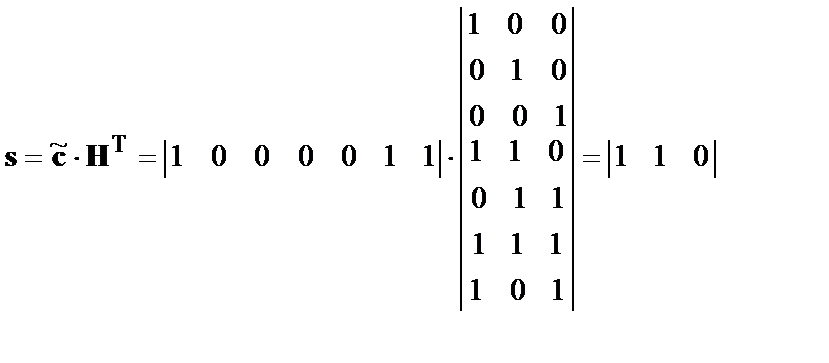Неравенство синдрома нулю свидетельствует об ошибке в канале, а код синдрома для простейших кодов, исправляющих однократные ошибки ( 
), определяет позицию «ошибочного» разряда (см. матрицу 
вида (6в) ), т. е. ошибка в разряде 
.
Таким образом, одним из способов задания линейных помехоустойчивых кодов является формирование порождающих или проверочных матриц. Способы задания таких матриц для наиболее распространенных разновидностей несистематических циклических кодов будут рассмотрены ниже.
Б. Полиномиальный способ описания линейных блоковых кодов
Полиномиальный способ используется для описания циклических кодов, нашедших ввиду простоты кодирования и декодирования наибольшее практическое применение.
Множество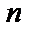 
-мерных канальных кодов 
( 
), его подмножество кодовых слов, заданное 
-мерными информационными словами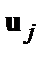 
( 
), множество 
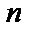-мерных векторов 
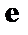канальных ошибок, а также порождающие эти коды конструкции (аналоги матриц 
и ) могут быть описаны с помощью полиномов (многочленов) произвольной степени вида
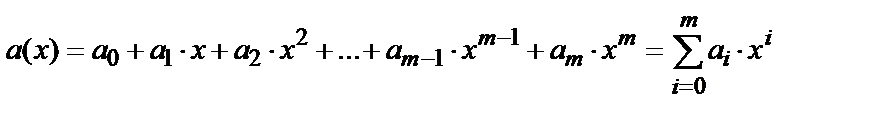, (8)
где 
– коэффициенты многочлена, принадлежащие алфавиту кода мощности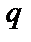 
.
Кодовое слово несистематического циклического кода формируется по соотношению (аналог матричного соотношения (2) )
, (9)
|
|
|
где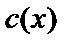 
– многочлен степени 
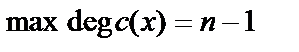, описывающий кодовые слова;
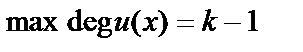– информационный многочлен степени 
;
– порождающий многочлен степени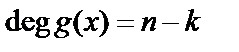 
;
и систематического кода – по соотношению
, 
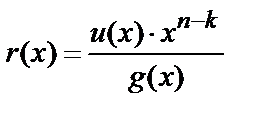, (10)
где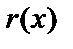 
– многочлен степени 
, описывающий младшие (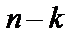 
) проверочных разрядов кода.
Примечание.
Обсудим особенности алгоритма деления многочленов.
Для каждой пары многочленов 
и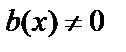 
( 
/ 
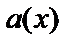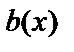) существует единственная пара многочленов 
(частное) и 
(остаток) таких, что
, 
.
Остаток, который представляет особый интерес, можно записать в виде
или 
. (11)
Отсюда многочлен 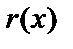(10) в терминах (11) может быть записан в виде
. (12)
Синдром 
(аналог матричного соотношения (7) ) с учетом (11) равен
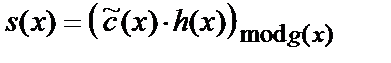, (13)
где 
– проверочный многочлен степени 
, такой что
(см. свойства расширенных конечных полей Галуа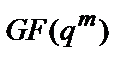 
).
Таким образом циклический код однозначно задается порождающим и проверочным многочленами.
Матричное представление простейшего систематического циклического кода аналогично рассмотренному выше примеру 4.
Рассмотрим особенности матричного описания простейшего несистематического циклического кода Коэффициенты порождающего и проверочного многочленов ( 
, 
и 
, 
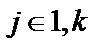) однозначно задают соответствующие ( 
)-мерную порождающую 
и ( 
)-мерную проверочную 
матрицы несистематического кода (их первые строки, а каждая следующая получается путем циклической сдвижки предыдущей вправо на один разряд), которые имеют вид
, 
. (14)
Пример 6.
Сформировать соответствующее информационному слову 
кодовое слово для несистематического циклического (7, 4, 3)-кода, порождаемого многочленом 
. Решение представить в полиномиальном и матричном виде. Оценить вектор синдрома для вектора ошибок 
(ошибка в разряде ).
|
|
|
Решение.
Полином, описывающий информационный код, имеет вид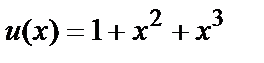 
. По (9) получим полином 
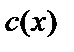, описывающий кодовое слово
,
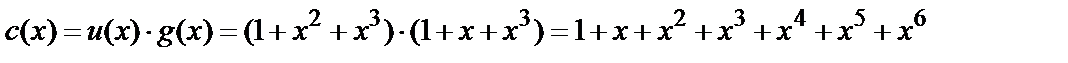т. е. кодовое слово имеет вид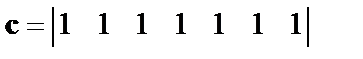 
.
Под воздействием помех в канале произошла ошибка в разряде и на приемной стороне получено канальное слово вида
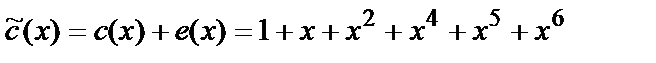или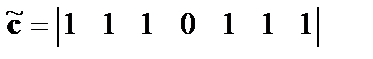 
.
Используя свойство поля Галуа получим проверочный полином 
.
По (13) оценим полином синдрома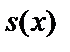 
.
Неравенство полинома синдрома 
нулю свидетельствует о наличии ошибки в принятом канальном слове.
Для наглядности отыскания ошибочного разряда решим задачу в матричном виде.
Сформируем по (14) порождающую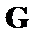 
и проверочную 
матрицы заданного несистематического циклического кода
, 
.
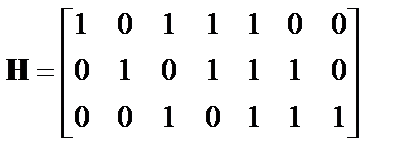Нетрудно показать, что кодовое слово 
, соответствующее информационному и порождаемое такой матрицей 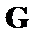равно 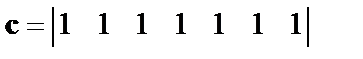. Появление ошибки в канале ( 
) позволяет сформировать канальный код .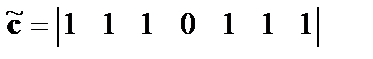
Как и прежде по соотношению (7) находим вектор синдрома
,
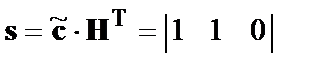значение которого по виду проверочной матрицы позволяет определить ошибочный разряд, а именно – , т. е. ошибка произошла в разряде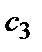 
.
Далее из канального слова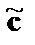 
восстанавливается кодовое слово 
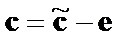, а результатом декодирования последнего является соответствующее информационное слово .
Особенности процесса декодирования несистематических циклических кодов будут рассмотрены позже. Принципы построения и описании работы кодеров и декодеров циклических кодов на основе порождающих и проверочных многочленов будут рассмотрены при изучении основных разновидностей циклических кодов.
2) Інформація – відомості про об'єкти, процеси і явища.
Інформація з обмеженим доступом – інформація, право доступу до якої обмежене встановленими правовими нормами і (або) правилами.
Конфіденційна інформація – інформація з обмеженим доступом, що знаходиться у володінні, користуванні або розпорядженні окремих фізичних (юридичних) осіб або держави, порядок доступу до якої встановлюється ними.
Секретна інформація – інформація з обмеженим доступом, що містить зведення, що складають державну або іншу передбачену законом таємницю.
|
|
|
Погроза для інформації – витік, можливість блокування або порушення цілісності інформації.
Витік інформації – неконтрольоване розповсюдження інформації, що веде до її несанкціонованого одержання.
Блокування інформації – виключення можливості санкціонованого доступу до інформації.
Порушення цілісності інформації – перекручування інформації, її руйнування або знищення.
Доступ до інформації – можливість одержання, обробки інформації, її блокування і (або) порушення цілісності.
Несанкціонований доступ до інформації – доступ до інформації, при якому порушуються встановлений порядок його здійснення і (або) правові норми.
Засіб технічного захисту інформації – пристрій і (або) програмний засіб, основне призначення яких – захист інформації від погроз.
Власнезахист інформації можна визначити як міри для обмеження доступу до інформації для яких-небудь осіб (категорій осіб), а також для посвідчення дійсності і незмінності інформації.
Інформація з погляду інформаційної безпеки має наступні категорії:
- конфіденційність - конкретна інформація, доступна тільки колу осіб, якій вона призначена; порушення цієї категорії визначається як розкрадання або розкриття інформації;
- цілісність - інформація існує у вихідному виді, тобто при її збереженні або передачі не було зроблено несанкціонованих змін; порушення цієї категорії називається фальсифікацією повідомлення;
- автентичність - джерелом інформації є саме та особа, що заявлена як її автор; порушення цієї категорії також називається фальсифікацією автора повідомлення;
- апелюємость - гарантія того, що при необхідності можна буде довести, що автором повідомлення є саме заявлена людина, і не може бути ніхто іншої (категорія, досить часто застосовувана в електронній комерції) (відмінність цієї категорії від попередньої полягає в тому, що в першому випадку при підміні автора повідомлення хтось іншої намагається представити себе автором, а в другому - сам автор намагається відмовитися від своїх слів).
|
|
|
|
|
|
