 |
§11. Названия и обозначения производных ступеней
|
|
|
|
§11. Названия и обозначения производных ступеней
Название любой производной ступени состоит из наименования основной ступени с добавлением названия соответствующего знака альтерации.
В записи по слоговой системе знак альтерации чаще заменяется словом «диез», «бемоль» и т. д. или же сохраняется знак, прибавленный к слогу, обозначающему тот или иной звук. Например:
фа-диез (или — фа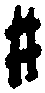 
), ре-бемоль (или 
),
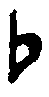до-дубль-диез (или — до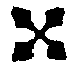 
), ля-дубль-бемоль (или ля 
).
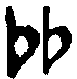В буквенной системе для обозначения знаков альтерации используются соответствующие приставки, добавляемые к буквам, дающим названия основных ступеней. Так,
| диез | обозн. прист. | is | напр | cis | =до-диез |
| дубль-диез | — »— — »— | isis | — »— | fisis | =фа-дубль-диез |
| бемоль | — »— — »— | es | — »— | ges | =соль-бемоль |
| дубль-бемоль | — »— — »— | eses | — »— | deses | =ре-дубль-бемоль |
Однако тут есть три исключения:
| вместо | aes | пишется | as | (=ля-бемоль) |
| — »— | ees | — »— | es | (=ми-бемоль) |
| — »— | bes | — »— | heses | (=си-дубль-бемоль)*. [Звук си-бемоль по буквенной нотации, как известно, обозначается буквой b. ] |
§ 12. Энгармонизм звуков
В равномерно-темперированном строе вследствие равенства всех полутонов (в каждой октаве) имеет место явление энгармонизма.
Энгармонизмом называется тождество звуков по высоте при их различном обозначении. Каждая ступень (как основная, так и производная) может быть заменена ступенью другого наименования, но высота звука при этом не изменится. Таких энгармонических замен у всех ступеней (если не считать их основных названий) может быть всего две, за исключением тона ля-бемоль, который может иметь только одну энгармоническую замену. Например:
|
|
|
до-диез=си-дубль-диез=ре-бемоль,
ми=фа-бемоль=ре-дубль-диез,
си-бемоль=ля-диез=до-дубль-бемоль и т. д.
В то же время: ля-бемоль=соль-диез (в данном случае других вариантов нет).
§ 13. Диатонические и хроматические тоны и полутоны
В зависимости от того, из звуков каких ступеней образованы те или иные тоны и полутоны, они делятся на два типа: диатонические и хроматические.
Диатоническими называются тоны или полутоны, образованные соседними по названию и написанию ступенями (то есть непременно звуками разных наименований). Например:
23 и т. п.
(диатонические полутоны)
24 и т. п.
(диатонические целые тоны)
Хроматическими называются тоны или полутоны, образованные звуками одной и той же ступени, но представленной в разных — основном и альтерированном, или с разнонаправленными альтерациями — видах, а также целые тоны, состоящие из звуков, расположенных через одну ступень друг от друга. Например:
25 и т. п.
(хроматические полутоны)
26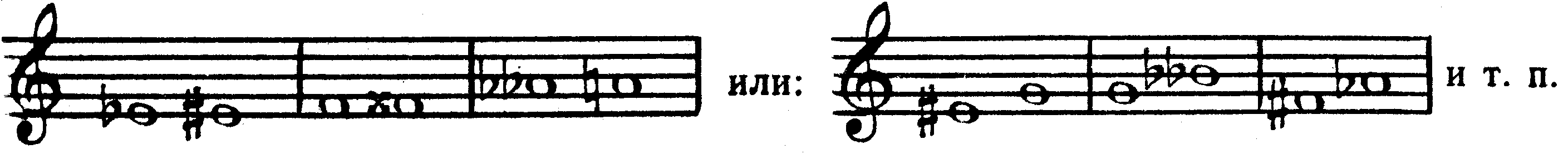 
(хроматические целые тоны)
Глава III. ВРЕМЕННЫЕ СООТНОШЕНИЯ В МУЗЫКЕ (РИТМ)
§ 14. Общие положения
Область ритма, метра, темпа — важнейшая сторона музыки — находится в прямой зависимости от ее временной природы. Всякое исполненное музыкальное произведение занимает то или иное время. Между частями музыкального целого образуются определенные временные соотношения. То же относится к другим видам временных искусств — к литературе, театру, кино. Огромное значение временных соотношений отличает эти виды искусств от пространственных (живописи, графики, скульптуры, архитектуры), произведения которых могут быть охвачены взглядом сразу.
Важнейшие проявления временных закономерностей отражаются в ритме произведения. Ритмом в музыке называется организация звуков и пауз по их длительностям. Любая последовательность звуков различной длительности (а в частном случае — и одинаковых длительностей) является проявлением ритма. Однако в музыке чаще используются ритмы, заключающие в себе, с одной стороны, соизмеримость длительностей, а с другой — ту или иную степень внутренней организованности, которая может быть выявлена путем повторности элементов, периодичности их появления.
|
|
|
Соизмеримость длительностей — понятие относительное, зависящее от близости или удаленности отдельных звуков по их временной значимости. Так, можно говорить о близости или соизмеримости четвертной и восьмой, четвертной и половинной, половинной и восьмой, всех их вместе между собой. Гораздо сложнее говорить о соизмеримости при восприятии на слух шестьдесятчетвертой и целой длительностей.
Вообще, трудно представить себе ритм, где очень мелкие и очень крупные длительности беспорядочно смешаны, — например:
28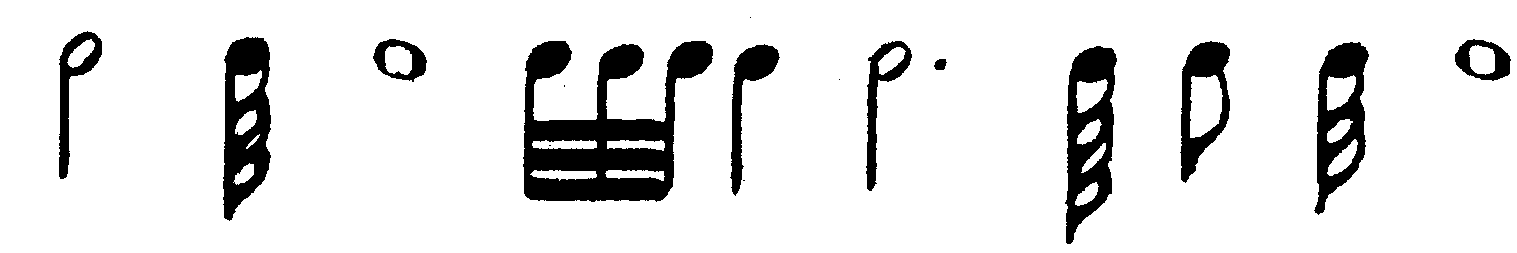 
Чисто математическая соизмеримость этих длительностей очевидна: в целой — 64 шестьдесятчетвертых, 2 половинных, 32 тридцатьвторых, в тридцатьвторой — 2 шестьдесятчетвертых или 4 стодвадцатьвосьмых, в четверти — 2 восьмых или 4 шестнадцатых и т. д. Однако если крупные длительности сопоставляются с мелкими, то обычно соизмеримость их обеспечивается объединением мелких длительностей в группы, равные по общей протяженности более крупным длительностям. Например:
|
|
|
