Главная | Обратная связь | Поможем написать вашу работу!

Оценка структурной надежности сети

Надежностью сети связи будем называть ее свойство, заключающееся в способности сети выполнять заданные функции (доставка сообщений,выдача справочной информации и т.д.) в определенных условиях эксплуатации.

Для сетей связи, являющихся сложными многофункциональными системами, можно выделить два основных аспекта надежности, которые условимся называть аппаратурным и структурным. Под аппаратурным аспектом будем понимать проблему надежности аппаратуры, отдельных устройств и их элементов, входящих в узлы и линии сети. Структурный аспект отражает функционирование сети в целом в зависимости от работоспособности или отказов узлов (станций, пунктов) или линий сети, т.е. он связан с возможность существования в сети путей доставки информации. В курсовом проекте будем рассматривать только структурную надежность сети связи.

В этом случае первичная сеть связи может быть представлена в виде вероятностного графа. Веса элементов графа (узлов и линий связи) представляются надежностными показателями. Например, коэффициентами готовности – К_г. Под коэффициентом готовности элемента сети понимается вероятность исправного (работоспособного) состояния данного элемента в произвольный момент времени в процессе эксплуатации. Для упрощения расчетов будем предполагать, что элементы сети, с точки зрения воздействующего фактора, являются статистически независимыми. На рисунке 6.1 представлена модель сети, используемая для оценки структурной надежности в курсовом проекте.

Рисунок 6.1 - Модель сети.

Как видно из модели сети, узлы кольца являются абсолютно надежными. Абсолютно надежны также РАТС и участки подключения РАТС к узлам кольца. Ненадежными являются различные участки кольца.

Коэффициенты готовности участков кольца могут быть рассчитаны по методике, изложенной в [10]. В курсовом проекте принимаем коэффициент готовности равный 0.99 или 0.999 на фиксированную длину участка кольца (L=5км; L=10км и т.д.).

В качестве показателя оценки структурной надежности будем использовать математическое ожидание числа связей М(Х) на ГТС. Для определения М(Х) воспользуемся следующим алгоритмом:

1. Определим максимальное число связей на ГТС. Для этого используем матрицу М, заполненную в разделе 5.2.

2. Определим списки путей, которые могут быть использованы для доставки информации от УК_i до УК_j сети в нормальных и аварийных условиях.

3. Для каждой пары узлов определим вероятность их связности.

4. Произведем суммирование значений вероятностей связности различных пар узлов сети.

В результате получим абсолютное значение математического ожидания числа связей сети – М(Х). Удобнее и нагляднее данную величину выразить в относительных единицах. Тогда величина М(Х)_отн. может быть рассчитана по формуле:

М(Х)_отн. = (М(Х)/N_max)·100%,

где N_max – максимальное (заданное) число связей в сети при условии, что все элементы сети абсолютно надежны и узлы связаны по принципу

«каждый с каждым».

N_max =m(m-1),

где m-число узлов коммутации(РАТС,АМТС и т.д.) на сети.

Для определения вероятности связности узла i с узлом j воспользуемся следующей методикой:

1. Определим список путей, которые могут быть использованы для связи узла i с узлом j.

2. Определим надежность каждого из указанных путей.

3. Воспользуемся формулой для расчета вероятности суммы совместных событий:

где t - число путей, которые могут быть использованы для связи узла i с узлом j;

А_к – событие, поставленное в соответствие i-ому исправному пути k=();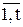

Р(А_к) – вероятность наступления события А_к;

Р(А_кÇ А_m) – вероятность совместного наступления двух событий А_к и А_m;

Р(А₁ Ç А₂ …А_t) – вероятность совместного наступления t событий Аi;

P(UA_k) – вероятность наступления хотя бы одного события А_к(к= ()).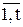

С учетом условия совместимости, показатели коэффициентов готовности элементов сети, входящих в любое из указанных выше выражений формулы для расчета вероятности суммы совместных событий, заменяется на первую степень.

Пример.

Определить математическое ожидание числа связей М(Х)_отн.для сети, представленной на рисунке 6.2, при условии, что используются все допустимые пути для связи узлов сети и коэффициент готовности каждой линии связи (ребер графа сети) равен К_г = 0,9.

Рисунок 6.2 - Структура сети.

Для решения задачи воспользуемся рассмотренным выше алгоритмом.

1. Определим список путей, связывающих узлы сети.

m¹₁₂={b₁₂}, m²₁₂ = {b₁₃,b₂₃}; m¹₁₃ = {b₁₃}, m²₁₃ = {b₁₂,b₂₃};

m¹₁₄ = {b₁₃, b₃₄}, m²₁₄ = {b₂₁,b₂₃,b₃₄}; m¹₂₁ = {b₁₂}, m²₂₁ = {b₁₃,b₂₃};

m¹₂₃ = {b₂₃}, m²₂₃ = {b₁₂,b₁₃}; m¹₂₄ = {b₂₃,b₃₄}, m²₂₄ = {b₁₂,b₁₃,b₃₄};

m¹₃₂ = {b₂₃}, m²₃₂ = {b₁₃,b₁₂}; m¹₃₁ = {b₁₃}, m²₃₁ = {b₁₂,b₂₃};

m¹₃₄ = {b₃₄}; m¹₄₁ = {b₁₃, b₃₄}, m²₄₁ = {b₁₂,b₂₃,b₃₄}; m¹₄₂ = {b₂₃,b₃₄},

m²₄₂ = {b₁₂,b₁₃,b₃₄}; m¹₄₃ = {b₃₄}.

2. Определим надежность каждого из указанных путей.

Н(m¹₁₂) = Н(m¹₂₁) = К₂₁, Н(m¹₁₃) = Н(m¹₃₁) = К₂₃,

Н(m¹₂₃) = Н(m¹₃₂) = К₂₃, Н(m¹₃₄) = Н(m¹₄₃) = К₃₄,

Н(m¹₁₄) = Н(m¹₄₁) = К_13* К₃₄, Н(m¹₂₄) = Н(m¹₄₂) = К_23* К₃₄,

Н(m²₁₂) = Н(m²₂₁) = К_13* К₂₃, Н(m²₁₄) = Н(m²₃₁) = К_21* К₂₃,

Н(m²₂₃) = Н(m²₃₂) = К_13* К₂₁, Н(m²₁₄) = Н(m²₄₁) = К_21* К_23* К₃₄,

Н(m²₂₄) = Н(m²₄₂) = К_21* К₁₃*К₃₄.

3. Определим вероятности связности для каждой пары узлов сети.

Р₁₂ = Р₂₁ = К₂₁ + К₁₃ К₂₃ - К₂₁ К₁₃ К₂₃;

Р₁₃ = Р₃₁ = К₁₃ + К₂₁ К₂₃ - К₂₁ К₁₃ К₂₃;

Р₁₄ = Р₄₁ = К₁₃ К₃₄ + К₂₁ К₂₃ К₃₄ – К₁₃ К₂₁ К₂₃ К₃₄;

Р₂₃ = Р₃₂ = К₂₃ + К₁₃ К₂₁ – К₁₃ К₂₁ К₂₃;

Р₂₄ = Р₄₂ = К₂₃ К₃₄ + К₂₁ К₁₃ К₃₄ – К₁₃ К₂₁ К₂₃ К₃₄;

Р₃₄ = Р₄₃ = К₃₄;

4. Определим математическое ожидание числа связей в сети М(Х).

М(Х) = Р₁₂+ Р₂₁+ Р₁₃ + Р₃₁ + Р₁₄ + Р₄₁+ Р₂₃ + Р₃₂ + Р₂₄ + Р₄₂+ Р₃₄ + Р₄₃.

Определим максимальное число связей в сети при абсолютно надежных элементах.

N = m (m-1) = 4 x 3 = 12.

Определим М(Х)_отн.,подставив значение К_г = 0,9 в выражение, полученное в пункте 4.

М(Х)_отн. = М(Х)/ (m (m-1)) 100% = (10.3576 /12) 100% = 86,31%

В курсовом проекте следует изобразить модель анализируемой сети и оценить структурную надежность кольца, используя в качестве показателя структурной надежности М(Х)_отн., а также указать способы повышения надежности сети.

Контрольные вопросы

1. Что понимается под структурной надежностью сети связи?

2. Какие модели сети используются для оценки структурной

надежности?

3. Укажите показатели, которые используются для количест-

венной оценки структурной надежности сети связи.

4. Поясните смысл значения коэффициента готовности участ-

ка сети SDH.

5. Какие исходные данные необходимы для расчета математи-

ческого ожидания числа связей в сети?

6. Перечислите основные способы повышения структурной

надежности.

Литература

1. Основные положения развития взаимоувязанной сети связи РФ на перспективу до 2005 года. Руководящий документ. Книга 3 - М.: ГКЭ, 1996.

2. Крук Б.И., Попантонопуло В.Н., Шувалов В.П. Телекоммуникационные сети и системы: Учебное пособие для вузов и колледжей.- Новосибирск: СиБГАТИ, 1997.

3. Синхронная цифровая иерархия. Учебное пособие под ред. Крука Б.И. – Новосибирск: Издательство СибГАТИ, 1998.

4. Слепов Н.Н. Синхронные цифровые сети SDH. –М.: Эко-трендз. 1998.

5. Заславский К.Е., Фокин В.Г. Проектирование оптической транспортной сети. Учебное пособие.-Новосибирск: СибГУТИ, 1999.

6. Нормы технологического проектирования. Городские и сельские телефонные сети. НТП 112-2000.-М.: ЦНТИ «Информсвязь», – 2000.

7. Соколов Н.А. Эволюция местных телефонных сетей. – Пермь: Книга, 1994.

8. Ионов А.Д. Волоконная оптика в системе связи и коммутации. Часть 1. Учебное пособие. – Новосибирск: СибГАТИ, 1998.

9. Линии передачи волоконно - оптические на магистральной и внутризоновоых первичных сетях ВСС России. Техническая эксплуатация. Руководящий технический материал. – М.: Минсвязи, Россия, 2000.

Приложение А

Средняя исходящая нагрузка для различных источников нагрузки.

№пп	Тип АЛ	Среднее количество вызовов в ЧНН на 1 АЛ (С)	Средняя продолжительность занятия в сек (t) с	Средняя интенсивность исходящей нагрузки на 1 АЛ в ЧНН, Эрл.	Время, используемое для расчета нагрузки
5 зн.	6 зн.	5 зн	6 зн.	5 зн	6 зн.
	Индивид. польз.	0,65 0,9	0,8 1,1	99,6		0,018 0,025	0,022 0,03	Утр.ЧНН; Веч. ЧНН
	Н/х сектор: “Деловой” “Спальный”	3,5 1,1	4,0 1,2	56,6 82,0		0,055 0,025	0,070 0,030	Утр.ЧНН, веч.время Веч.ЧНН, утр.время
	Таксофон местной связи	7,5 8,0	9,5 10,5			0,15 0,2	0,2 0,27	Дневн. ЧНН Вечерн.ЧНН
	Таксофон междугородный (исходящей связи)					0,65	0,65	Дневн. ЧНН Вечерн.ЧНН
	Районный переговорный пункт с серийным исканием					0,6	0,6	Веч. ЧНН, утр.время
	Линии от малых УАТС, подключаемых к станции на правах абонента					0,15	0,15	Утр.ЧНН, веч.время
	Устройство передачи данных (соединен. по телеф. алгоритму)					0,15	0,15

Приложение Б

Нормы, используемые при расчете нагрузки по различным направлениям на ГТС.

h_i, %	K_i, %	h_I, %	K_i, %
9,5	26,4		38,5
10,1	27,4		42,4
10,2	27,6
	28,3		50,4
			54,5
	31,5		58,2
	32,9		61,8
	33,3

Приложение В

Таблица первой формулы Эрланга

V Емк. пучка	Интенсивность поступающей нагрузки при потерях Р
0,0001	0,001	0,002	0,003	0,005	0,010
	0,452	0,761	0,898	1,0	1,126	1,347
	0,73	1,15	1,32	1,4	1,61	1,89
	1,05	1,58	1,79	1,9	2,15	2,48
	1,42	2,05	2,31	2,4	2,72	3,10
	1,83	2,56	2,85	3,0	3,32	3,75
	2,26	3,09	3,42	3,6	3,94	4,42
	2,72	3,85	4,01	4,22	4,59	5,11
	3,21	4,23	4,63	4,92	5,25	5,82
	3,71	4,83	5,26	5,52	5,93	6,54
	4,24	5,44	5,91	6,27	6,93	7,28
	4,78	6,07	6,57	6,9	7,34	8,03
	5,34	6,72	7,24	7,63	8,06	8,79
	6,50	8,04	8,63	9,05	9,53	10,33
	7,70	9.40	10,05	10,49	11,04	11,91
	8,95	10,80	11,50	11,95	12,57	13,52
	10,23	12,23	12,96	13,5	14,13	15,14
	11,54	13,69	14,49	15,1	15,72	16,79
	12,88	15,17	16,02	16,6	17,32	18,45
	14,24	16,67	17,57	18,25	18,94	20,13
	15,63	18,19	19,14	19,82	20,57	21,83
	17,04	19,72	20,72	21,25	22,22	23,53
	18,47	21,28	22,32	23,4	23,89	25,25
	19,92	22,84	23,93	24,8	25,56	26,98
	21,39	24,42	25,55	26,25	27,25	28,72
	22,86	26,01	27,18	28,1	28,94	30,46
	24,33	27,61	28,82	29,7	30,64	32,22
	25,83	29,23	30,48	31,5	32,36	33,98
	27,34	30,85	32,14	33,5	34,08	35,75
	28,86	32,48	33,81	34,5	35,80	37,52
	30,40	34,12	35,49	36,5	37,54	39,30
	31,94	35,77	37,17	38,53	39,28	41,09
	33,49	37,42	38,86	39,6	41,02	42,88
	35,05	39,09	40,56	41,5	42,78	44,68
	36,63	40,75	42,27	43,5	44,53	46,48

Продолжение таблицы приложения В.

V	Интенсивность поступающей нагрузки при потерях Р
0,0001	0,001	0,002	0,003	0,005	0,010
	40,58	44,95	46,56	47,8	48,95	51,00
	44,58	49,19	50,88	52,4	53,39	55,55
	48,62	53,46	55,23	56,3	57,86	60,12
	52,69	57,75	59,60	61,5	62,35	64,71
	56,73	62,07	64,00	65,1	66,86	69,31
	60,93	66,42	68,42	70,5	71,40	73,94
	65,08	70,78	72,86	73,4	75,94	78,57
	69,27	75,17	77,32	78,5	80,51	83,22
	78,47	80,00	81,79	82,5	85,08	87,88
	77,69	83.99	86,28	87,3	89,67	92,55
	81,94	88,42	90,78	92,4	94,27	97,24
	86,20	92,87	95,30	97,3	98,88	101,93
	90,5	97,3	99,8	99,4	103,5	106,6
	94,8	101,8	104,4	102,6	108,1	111,3
	99,1	106,3	108,9	110,4	112,8	116,1
	103,4	110,8	113,5	115,1	117,5	120,8
	112,1	119,8	122,7	123,8	126,8	130,3
	120,8	128,9	131,8	134,5	136,1	139,8
	129,6	138,0	141,0	143,6	145,5	149,3
	138,4	147,1	150,3	151,4	154,9	158,8
	147,3	156,2	159,5	162,1	164,4	168,4
	156,2	165,4	168,8	170,8	173,8	177,9
	165,1	174,6	178,1	180,6	183,7	187,5
	174,0	183,9	187,4	190,1	192,7	197,1
	183,0	193,1	196,8	200,5	202,2	206,7
	192,0	202,4	206,2	208,4	211,7	216,4
	201,0	211,7	215,6	218,8	221,3	226,6
	246,4	258,3	262,7	267,3	269,1	274,3
	292,4	305,4	310,2	314,5	317,1	322,9
	338,4	352,7	357,2	362,4	365,3	371,6

Приложение Г

Величины коэффициентов a и b в формуле О^’Делла

при различных значениях D_эф и Р

D_эф	Р=0,001	Р=0,003	Р=0,005	Р=0,01
a	b	a	b	a	b	a	b
	5,62	1,5	4,27	1,3	3,76	1,2	3,16	1,1
	3,98	1,9	3,13	1,7	2,88	1,6	2,51	1,5
	3,16	2,3	2,63	2,1	2,41	2,0	2,15	1,9
	2,68	2,7	2,25	2,5	2,13	2,4	1,93	2,2
	2,37	3,1	2,07	2,9	1,93	2,7	1,77	2,5
	2,15	3,5	1,90	3,2	1,8	3,0	1,66	2,7
	1,99	3,8	1,79	3,5	1,7	3,3	1,58	2,9
	1,87	4,2	1,7	3,8	1,62	3,6	1.52	3,1
	1,78	4,5	1,62	4,1	1,55	3,9	1,46	3,3
	1,71	4,8	1,56	4,4	1,50	4,2	1,42	3,5
	1,64	5,1	1,51	4,7	1,46	4,4	1,39	3,7
	1,58	5,4	1,47	4,9	1,42	4,6	1,37	3,9
	1,54	5,7	1,44	5,1	1,39	4,8	1,33	4,1
	1,47	6,3	1,38	5,5	1,34	5,2	1,29	4,5
	1,41	6,9	1,34	5,9	1,30	5,6	1,25	4,9
	1,37	7,3	1,3	6,3	1,27	6,0	1,23	5,3
	1,33	7,7	1,27	6,7	1,25	6,4	1,21	5,6
	1,30	8,1	1,25	7,1	1,23	6,8	1,19	5,8
	1,28	8,5	1,23	7,5	1,21	7,2	1,17	6,0
	1,26	8,9	1,21	7,9	1,19	7,5	1,16	6,2
	1,24	9,3	1,2	8,2	1,18	7,7	1,15	6,4
	1,21	10,1	1,18	8,8	1,16	8,1	1,13	6,8
	1,19	10,9	1,17	9,1	1,14	8,5	1,12	7,2
	1,15	12,2	1,1	9,7	1,11	10,0	1,09	8,2

Приложение Д

⇐ Предыдущая 3 4 5 6 7 8 91011 12 Следующая ⇒

Воспользуйтесь поиском по сайту: